4.3. Методы Ньютона-Котеса
Способ получения
формул для вычисления приближенного
значения интеграла в методах Ньютона-Котеса
состоит в следующем. Разобьем отрезок
интегрирования
на
частичных (как правило, равных по длине)
отрезков, точки разбиения
,
,
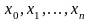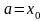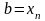будем называть узлами
интегрирования,
а расстояния между узлами
,
,
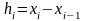– шагами
интегрирования.
В частном случае шаг интегрирования
может быть постоянным
.
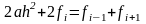На каждом из частичных отрезков
интегрирования
,
,
будем аппроксимировать подынтегральную
функцию полиномом некоторой степени.
В результате вычисление частичных
интегралов на отрезках
,
,
по формуле (4.1) не составит труда.
4.3.1. Методы прямоугольников
Рассмотрим
простейшие методы из класса методов
Ньютона-Котеса, в которых подынтегральную
функцию
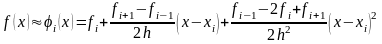на отрезках интегрирования
,
,
заменяют полиномом нулевой степени
(константой):
.
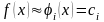Подставляя
в формулу (4.1) и выполняя интегрирование,
получаем
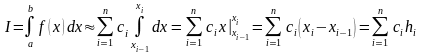. (4.2)
Таким образом, в
геометрической интерпретации приближенное
значение интеграла определяется суммой
площадей прямоугольников, одна из сторон
которых соответствует отрезкам
интегрирования длиной
,
а другая – аппроксимирующим константам.
Отсюда происходит и название методов.
Далее будем использовать обозначения:
,
,
.
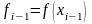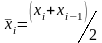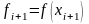Замечание. Формулу (4.2) можно также вывести, если заменить определенный интеграл интегральной суммой, непосредственно опираясь на определение понятия определенного интеграла.
Заметим, что замена
подынтегральной функции константой
неоднозначна, так как ее можно выбрать
равной значению подынтегральной функции
в любой точке каждого частичного отрезка
интегрирования. Выбирая константу
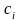равной значению подынтегральной функции
в левой (рис. 4.4 а) или правой (рис. 4.4 б)
границах отрезков
,
,
приходим к формулам левых
и правых
прямоугольников,
соответственно:
,
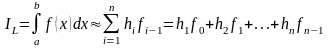(4.3)
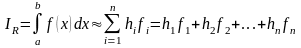. (4.4)
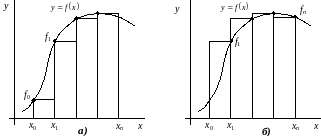
Рис. 4.4. Пример метода левых (а) и правых (б) прямоугольников.
В случае постоянного
шага интегрирования, когда
,
,
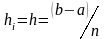формулы (4.3) и (4.4) приобретают вид
,
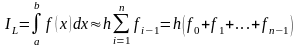(4.5)
.
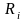На рис. 4.5 закрашенными фигурами показаны примеры погрешности вычисления значений интеграла методами левых и правых прямоугольников.
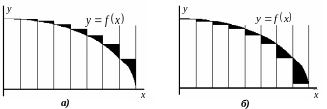
Рис. 4.5. Пример погрешности метода левых (а) и правых (б) прямоугольников.
Наиболее широко
на практике используется формула средних
прямоугольников,
в которой значение константы
(высоты прямоугольника) выбирается
равной значению подынтегральной функции
в средней точке
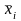каждого частичного отрезка интегрирования
,
:
.
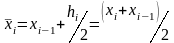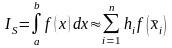Пример геометрической интерпретации метода средних прямоугольников представлен на рис. 4.6.
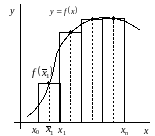
Рис. 4.6. Пример метода средних прямоугольников.
В случае постоянного шага интегрирования, когда , , формула средних прямоугольников будет иметь следующий вид
,
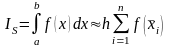где
,
.
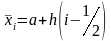Из трех рассмотренных выше методов в подавляющем большинстве случаев метод средних прямоугольников является наиболее точным.
Замечание. Если подынтегральная функция задана не аналитическим выражением, а таблично, то формула средних прямоугольников оказывается неприменима (без привлечения дополнительной интерполяции), так как значения функции известны лишь в узловых точках. В этом случае пользуются либо формулами левых или правых прямоугольников, либо используют другие методы.