
- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
4.5. Вычисление интегралов с заданной точностью
Используя приведенные
в разд. 4.4 оценки погрешности вычисления
интегралов, можно априори определить
шаг интегрирования
,
при котором погрешность вычисленного
результата гарантированно не превысит
некоторую заданную погрешность
.
Однако на практике пользоваться
априорными оценками погрешности не
всегда удобно, в таких случаях контроль
за точностью получаемого результата
можно организовать следующим образом.
Пусть вычисления проводились с постоянным
шагом
и
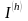 – вычисленное с шагом
приближенное значение интеграла
– вычисленное с шагом
приближенное значение интеграла
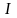 .
Если затем вычислить приближенное
значение
.
Если затем вычислить приближенное
значение
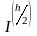 с шагом
,
то в качестве оценки погрешности
последнего вычисленного значения можно
рассматривать величину
с шагом
,
то в качестве оценки погрешности
последнего вычисленного значения можно
рассматривать величину
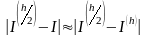 .
.
При необходимости
вычислить результат с заданной точностью
вычисления повторяют с последовательно
уменьшающимся (обычно вдвое) шагом
до тех пор, пока не выполнится условие
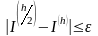 .
.
Можно применить указанное правило для контроля за погрешностью на каждом частичном отрезке , . При этом длина очередного шага , посредством последовательного уменьшения начальной длины вдвое, устанавливается такой, чтобы выполнялось неравенство
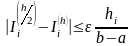 .
.
Тогда, в худшем случае, ошибка вычисления значения интеграла на всем отрезке интегрирования не будет превосходить сумму локальных погрешностей
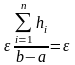 ,
,
то есть не будет превосходить заданного уровня погрешности.
Способ вычисления интеграла с автоматическим выбором шага имеет то преимущество, что он «приспосабливается» к особенностям подынтегральной функции: в областях резкого изменения функции шаг уменьшается, а там, где функция меняется слабо, – увеличивается. Такого рода алгоритмы называются адаптивными, то есть приспосабливающимися, их использование позволяет сократить затраты вычислительных ресурсов без потери точности вычисления.
Одним из подходов к экономии вычислительных ресурсов ЭВМ при необходимости сокращения шага интегрирования вдвое является сохранение в памяти ЭВМ результатов промежуточных вычислений для исходного шага и дополнение их результатами расчетов, связанных с введением на отрезках интегрирования дополнительных точек, располагающихся в их середине.
4.6. Особые случаи численного интегрирования
Интегрирование
разрывных функций.
Если подынтегральная функция в некоторых
внутренних точках
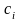 (
(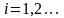 )
отрезка интегрирования
имеет разрыв первого рода (скачок), то
интеграл следует вычислять для каждого
участка непрерывности отдельно, а
результаты складывать. Например, в
случае одной точки разрыва (рис. 4.9)
)
отрезка интегрирования
имеет разрыв первого рода (скачок), то
интеграл следует вычислять для каждого
участка непрерывности отдельно, а
результаты складывать. Например, в
случае одной точки разрыва (рис. 4.9)
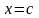 (
(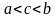 )
имеем
)
имеем
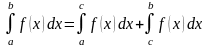 .
.
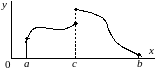
Рис. 4.9. Пример функции, имеющей разрыв первого рода в точке .
Для вычисления каждого из интегралов в правой части полученного равенства можно использовать любой из рассмотренных в данной главе методов.
Несобственные
интегралы.
К такому типу интегралов относятся
интегралы, которые имеют хотя бы один
бесконечный предел интегрирования или
подынтегральную функцию, имеющую разрыв
второго рода – обращающуюся в бесконечность
хотя бы в одной точке отрезка интегрирования.
Рассмотрим интеграл с бесконечной
границей интегрирования, например
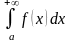 .
.
Один из универсальных способов вычисления подобных интегралов заключается в их представлении в виде суммы двух интегралов:
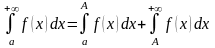
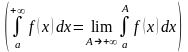 ,
,
где – некоторое большое положительное число, рис. 4.10.

Рис. 4.10. Иллюстрация вычисления интеграла с бесконечной границей интегрирования.
Вычисление первого
интеграла на конечном отрезке
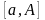 не вызывает затруднений. Выбор числа
производят таким образом, чтобы в
пределах допустимой погрешности вторым
интегралом можно было пренебречь.
не вызывает затруднений. Выбор числа
производят таким образом, чтобы в
пределах допустимой погрешности вторым
интегралом можно было пренебречь.
В случае, когда подынтегральная функция обращается в бесконечность в некоторой точке ( ) отрезка интегрирования , интеграл можно приближенно представить в виде суммы двух интегралов
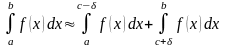 ,
,
где
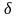 – некоторая достаточно малая положительная
величина, рис. 4.11.
– некоторая достаточно малая положительная
величина, рис. 4.11.
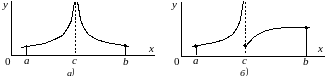
Рис. 4.11. Подынтегральная функция обращается в бесконечность в некоторой точке отрезка интегрирования: а) с двух сторон от нее; б) с одной стороны от нее.
На отрезках
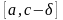 и
и
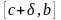 подынтегральная функция не имеет
особенностей и соответствующие интегралы
могут быть вычислены с помощью любого
из рассмотренных в данной главе методов.
подынтегральная функция не имеет
особенностей и соответствующие интегралы
могут быть вычислены с помощью любого
из рассмотренных в данной главе методов.
Замечание. В некоторых случаях при вычислении несобственных интегралов подходящая замена переменной интегрирования позволяет вообще избавиться от рассмотренных выше особенностей. Так, например, при вычислении интеграла
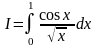
имеется особенность
в точке
![]() ,
где подынтегральная функция обращается
в бесконечность. Заменой переменной
,
где подынтегральная функция обращается
в бесконечность. Заменой переменной
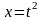 (
(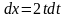 )
приходим к интегралу
)
приходим к интегралу
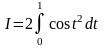 ,
,
который не имеет особенностей и вычисляется с требуемой точностью с применением любого из рассмотренных в данной главе методов.
