
- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
Глава 4. Численное интегрирование
Задачи, в которых требуется вычисление интегралов, возникают почти во всех областях прикладной математики, например, многие критерии оценки качества проектируемого изделия вычисляются с помощью определенных интегралов, в теории вероятности интеграл от функции плотности вероятности определяет вероятность некоторого события, с помощью интегралов вычисляются геометрические характеристики объектов и т.д. Иногда удается найти аналитическую формулу для вычисления определённого интеграла функции, но значительно чаще этого сделать не удается. В таких ситуациях требуется применять различные методы численного интегрирования функций.
Задача численного интегрирования заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. В настоящее время разработано большое количество методов численного интегрирования функций, учитывающих различные особенности в постановке соответствующей задачи. В данной главе будут рассмотрены некоторые из подходов, в частности, приведены формулы вычисления интегралов, основанные на полиномиальной аппроксимации подынтегральной функции.
4.1. Понятие определенного интеграла
Перед тем как
приступить непосредственно к рассмотрению
методов численного интегрирования,
рассмотрим теоретические основы,
приводящие к понятию определенного
интеграла. Пусть на отрезке
задана функция
.
Разобьем отрезок
на
отрезков точками
,
,
…,
следующим образом
,
причем
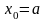 ,
а
,
а
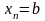 .
На каждом отрезке
.
На каждом отрезке
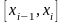 ,
,
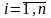 ,
выберем некоторую точку
,
выберем некоторую точку
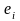 ;
обозначим длину данного отрезка через
;
обозначим длину данного отрезка через
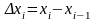 .
Сумму вида
.
Сумму вида
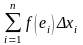 будем называть интегральной суммой для
функции
на отрезке
.
Очевидно, что интегральная сумма зависит
как от способа разбиения отрезка
точками
,
,
…,
,
так и от выбора точек
будем называть интегральной суммой для
функции
на отрезке
.
Очевидно, что интегральная сумма зависит
как от способа разбиения отрезка
точками
,
,
…,
,
так и от выбора точек
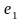 ,
,
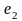 ,
…,
,
…,
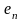 на каждом из отрезков разбиения
,
.
на каждом из отрезков разбиения
,
.
Пусть функция
неотрицательна на
,
тогда отдельное слагаемое
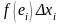 интегральной суммы равно площади
интегральной суммы равно площади
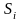 прямоугольника со сторонами
прямоугольника со сторонами
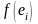 и
и
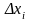 ,
.
В результате значение интегральной
суммы равно суммарной площади под
кусочной линией, образованной на каждом
из отрезков
соответствующей прямой
,
.
В результате значение интегральной
суммы равно суммарной площади под
кусочной линией, образованной на каждом
из отрезков
соответствующей прямой
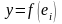 ,
параллельной оси абсцисс, рис. 4.1. Для
выбранного разбиения отрезка
обозначим через
,
параллельной оси абсцисс, рис. 4.1. Для
выбранного разбиения отрезка
обозначим через
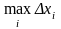 максимальную из длин отрезков
,
(«диаметр разбиения»).
максимальную из длин отрезков
,
(«диаметр разбиения»).
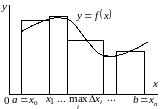
Рис. 4.1. Графическая иллюстрация интегральной суммы.
Определение 4.1.
Пусть предел интегральной суммы при
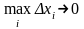 существует, конечен и не зависит от
способа выбора точек
,
,
…,
,
а также
,
,
…,
.
Тогда этот предел называется определенным
интегралом от функции
на отрезке
,
обозначается
существует, конечен и не зависит от
способа выбора точек
,
,
…,
,
а также
,
,
…,
.
Тогда этот предел называется определенным
интегралом от функции
на отрезке
,
обозначается
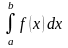 ,
а сама функция
называется интегрируемой на отрезке
,
то есть
,
а сама функция
называется интегрируемой на отрезке
,
то есть
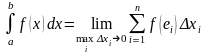 .
.
С геометрической
точки зрения значением определенного
интеграла является площадь криволинейной
трапеции – фигуры, ограниченной графиком
функции
и прямыми
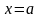 ,
,
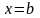 и
и
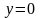 (рис. 4.2).
(рис. 4.2).
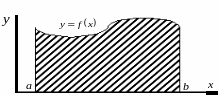
Рис. 4.2. Геометрическая интерпритация определенного интеграла.
Рассмотрим общий подход к решению задачи вычисления определенного интеграла. Введем в рассмотрение некоторую ломаную, которая расположена достаточно близко к кривой на отрезке , рис. 4.3.
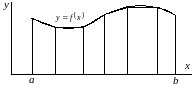
Рис. 4.3. Ломаная линия в геометрической интерпритации определенного интеграла.
Фигура под ломаной состоит из элементарных геометрических фигур (трапеций и прямоугольников), площадь которых может быть вычислена с помощью формул планиметрии. Поскольку ломаная выбрана достаточно близко к кривой , то суммарная площадь фигур под ней и значение соответствующего интеграла приближенно равны. Данное равенство оказывается тем более точным, чем ближе расположена ломаная к исходной кривой. Приведенные рассуждения носят качественный характер, для их использования на практике необходимо уточнить то, что описано нестрого: процедуру выбора ломаной и последующий переход к пределу.
В общем случае при
реализации численных алгоритмов
вычисления определенных интегралов от
некоторой функции
на отрезке
полагаем, что на
выбрана система точек
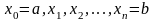 и
и
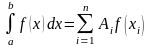 .
Формулы такого вида называются
квадратурными, коэффициенты
.
Формулы такого вида называются
квадратурными, коэффициенты
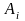 и точки
,
,
выбираются так, чтобы минимизировать
погрешность вычисления интеграла.
и точки
,
,
выбираются так, чтобы минимизировать
погрешность вычисления интеграла.
