Глава 1. Численные методы и особенности использования эвм в решении математических задач

Перед тем как приступить к непосредственному изучению численных методов рассмотрим их назначение, роль в математическом моделировании, а также особенности реализации с использованием вычислительной техники.

1.1. Математическое моделирование и численные методы

Моделирование – это описание исследуемого процесса, явления или объекта с использованием некоторого языка. Математическое моделирование – это описание исследуемого процесса, явления или объекта с применением формально-логических средств математики. Рассматривая математическую формализацию некоторого явления реального мира как своего рода теоретический эксперимент, а также основываясь на общих и достаточно естественных соображениях, в процессе исследования и математического моделирования данного явления можно выделить несколько основных этапов.

Формирование математической модели явления (процесса, объекта) – модели, представляющей собой математические закономерности, с помощью которых описаны основные характеристики моделируемого явления. Математическая модель любого изучаемого явления по причине его сложности и наличия связей с другими явлениями должна охватывать не все, а лишь важнейшие для рассматриваемой исследовательской задачи стороны, параметры и характеристики явления. Если математическая модель выбрана или разработана недостаточно тщательно, то какие бы методы не применялись для дальнейших расчетов, полученные при использовании модели результаты будут ненадежными, а в отдельных случаях и неверными.

Проведение математического исследования разрабатываемой модели явления и получение решения соответствующей исследовательской задачи. На данном этапе моделирования, в зависимости от сложности рассматриваемой модели, применяют различные подходы к ее исследованию и различный смысл вкладывается в понятие решения задачи. Например, получение доказательства существования или единственности решения в определенном смысле решает исследовательскую задачу (в том числе может приводить к получению алгоритма ее решения), однако не исключает проблему изучения качественного поведения решения и оценки его количественных характеристик.

Для наиболее грубых и несложных (в некотором смысле) моделей удается получить аналитическое решение задачи. Для более точных и сложных моделей аналитическое решение удается получить сравнительно редко. В такой ситуации при теоретическом анализе задачи пользуются приближенными алгоритмами, основанными на математических методах. Такие приемы позволяют представить приближенное решение в аналитической форме и с его помощью получить удовлетворительные численные результаты. Для наиболее точных и сложных моделей основными методами решения являются численные методы, требующие проведения большого объема вычислений на ЭВМ. Эти методы позволяют добиться хорошего количественного и даже качественного результата, но как правило их недостатком является получение некоторого частного решения задачи.

Анализ состоятельности предложенной модели подразумевает исследование результатов решения и сопоставление полученного решения с имеющимися данными физического эксперимента. На данном этапе оценивается состоятельность математической модели и проведенного исследования (по степени их соответствия параметрам изучаемого явления). «Хорошее» согласование с результатами экспериментов обычно свидетельствует о правильности выбора или тщательности разработки модели. В противном случае необходимы дополнительные уточнения, изменения, доработки модели, повторение предыдущих этапов исследования и т.д.

На рис. 1.1 приведена схема, отражающая взаимосвязь этапов исследования и математического моделирования с различными математическими методами.

Рис. 1.1. Взаимосвязь этапов математического моделирования явления.

Как видно из представленной на рис. 1.1 схемы, каждый этап исследования и математического моделирования явления в конечном итоге может быть связан с использованием численных методов и получением численного решения задачи.

Представленный выше материал позволяет акцентировать внимание на двух аспектах дисциплины «Численные методы»: математическое моделирование и необходимость использования в процессе исследования ЭВМ. В то же время одной из характерных особенностей современного математического моделирования является широкое применение ЭВМ для решения научных, технических и экономических задач. В результате, численные методы имеют непосредственную связь с математическим моделированием явлений реального мира и решением с помощью ЭВМ различных исследовательских задач данных явлений. При этом следует отметить, что ЭВМ не «решает задачу» (в том смысле, который обычно вкладывается в данное понятие), а лишь выполняет программы, реализующие вычислительные алгоритмы, основу многих из которых часто составляют именно численные методы.

Численные методы – это методы приближенного или точного решения задач теоретической или прикладной математики, основанные на построении конечной последовательности действий над конечным множеством чисел.

Численные методы являются предметом изучения вычислительной математики, которая зародилась еще в глубокой древности. Современная вычислительная математика состоит из многих разделов, важнейшими из которых являются: вычисление значений функций, вычислительные методы линейной алгебры, численное решение алгебраических и трансцендентных уравнений, численное дифференцирование и интегрирование, численное решение дифференциальных и интегральных уравнений, численные методы поиска экстремумов функций и т.д.

До появления ЭВМ основные усилия ученых были направлены на поиск решений в явном виде. Однако, в математике часто встречаются задачи, решение которых не удается получить в виде формулы, связывающей искомые величины с заданными значениями переменных. Для их решения стремятся найти некоторый бесконечный процесс, сходящийся к искомому ответу. Если такой процесс задан или выявлен, то, выполняя некоторое количество шагов, а затем прекращая вычисления, получают приближенное решение задачи. Соответствующая процедура связана с проведением вычислений по определенной системе правил, которая называется алгоритмом.

Такой подход к решению задач был известен еще до появления ЭВМ, но применялся весьма редко из-за исключительной трудоемкости. Применение численных методов на базе ЭВМ существенно расширило класс задач, допускающих исчерпывающий анализ. Теперь исследователю при построении математической модели не нужно стремиться к сильным упрощениям, которые были необходимы раньше для получения ответа в явном виде. Его внимание, прежде всего, должно быть направлено на то, чтобы правильно учесть все наиболее существенные особенности изучаемого объекта. Далее исследователь выполняет разработку алгоритма или принимает решение о целесообразности использования готового алгоритма решения соответствующей задачи, а затем осуществляет реализацию алгоритма на ЭВМ.

Для иллюстрации алгоритмического подхода к решению математических задач рассмотрим простой пример, связанный с задачей вычисления числа . Как известно, вычисление числа сводится к расчету периметров правильных многоугольников, вписанных в окружность с диаметром 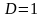и описанных вокруг нее. Пусть – периметр вписанного, а – описанного правильного 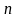-угольника. Так, например, для правильных шестиугольников , следовательно, .

С увеличением числа вершин значения периметров 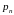увеличиваются, а 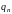– убывают, стремясь в пределе к значению : . Таким образом, периметры определяют число с недостатком, а с избытком: . Полученная двухсторонняя оценка значения позволяет легко контролировать точность на каждом шаге вычисления, выполняемом с увеличением значения на единицу. Погрешность вычисления числа в зависимости от значения может быть оценена соотношением .

Приведем некоторые факты из истории вычисления числа . Великий древнегреческий ученый Архимед дошел до вычисления периметров правильных 96-угольников и получил следующую двухстороннюю оценку : . К первой половине XV века в знаменитой обсерватории под Самаркандом придворный астроном Ал-Каши вычислил с 17 знаками после запятой. К концу XIX века английский математик В.Шенкс вычислил 707 знаков , затратив на это более 15 лет. В настоящее время с помощью ЭВМ число вычислено с точностью, измеряемой сотнями тысяч знаков.

Понятие решения задачи с помощью ЭВМ включает в себя гораздо больше, нежели просто вычисления на ЭВМ. Для решения и исследования математических задач с использованием ЭВМ в настоящее время принята и представляется наиболее эффективной методология, представленная на рис. 1.2.

Рис. 1.2. Этапы решения математических задач с применением ЭВМ.

Рассмотрим содержание представленных на рис. 1.2 этапов решения и исследования математических задач с использованием ЭВМ.

Постановка задачи и определение конечных целей является наиболее важным и ответственным этапом решения задачи, на котором реализуется выбор общего подхода к ее решению, определяются основные критерии, которым должна удовлетворять разрабатываемая математическая модель, дается формальное математическое описание самой задачи и предполагаемого результата ее решения.

Составление математической модели объекта исследования. На данном этапе обычно строится континуальная математическая модель, сформулированная в терминах дифференциальных, трансцендентных или алгебраических уравнений для функций непрерывного аргумента. Такая модель является наиболее экономичным способом описания исследуемого объекта или явления.

Дискретизация математической модели часто вызвана особенностями ЭВМ, имеющих ограниченную разрядную сетку памяти. Переход от континуальной модели к дискретной заключается в замене функций непрерывного аргумента функциями дискретного аргумента. Например, интеграл заменяется конечной суммой, производные – разностными отношениями и т.д.

Разработка численного метода и вычислительного алгоритма. Математическая формулировка задачи может оказаться непредставимой на компьютере, так как ЭВМ способна выполнять только элементарные арифметические операции. Поэтому такие общеизвестные математические понятия как тригонометрические функции, квадратные корни, логарифмы, корни уравнений и т.д. должны быть выражены через элементарные арифметические операции сложения, вычитания, деления и умножения. Задача данного этапа заключается в разработке или выборе вычислительного алгоритма и численного метода, реализующего некоторый математический метод решения задачи.

Программирование для ЭВМ. Назначение данного этапа состоит в том, что численный метод и вычислительный алгоритм решения задачи необходимо «переложить» на язык, понятный ЭВМ, то есть закодировать его на некотором алгоритмическом языке программирования.

Отладка программы. На данном этапе производится тестирование программы с целью обнаружения и устранения допущенных ошибок.

Вычислительные эксперименты заключаются в том, что с использованием разработанной программы на основании наборов исходных данных производится необходимое количество расчетов на ЭВМ.

Интерпретация результатов. На данном этапе полученные результаты расчетов подвергаются всестороннему анализу, на основании которого для решаемой задачи либо получается полный «ответ», либо выявляются некоторые особенности поведения исследуемого объекта или явления, требующие повторных экспериментов на ЭВМ. Достаточно часто возникает необходимость в изменении постановки задачи, что приводит к полному повторению всех перечисленных выше этапов ее решения.

Содержание рассмотренных выше этапов «решения задачи» с помощью ЭВМ позволяет сделать следующие выводы:

1. ЭВМ задач не решает, она производит заранее определенную последовательность вычислений по заданному алгоритму.

2. Использование ЭВМ не освобождает исследователя от необходимости тщательного осмысления своей работы, изучения исследуемого объекта и разделов математики, касающихся решения задачи. Машина может производить вычисления быстрее и точнее человека, но она не способна решать, какой должна быть программа вычислений или что делать с полученными результатами.

Сформулируем наиболее важные проблемы вычислительной математики:

1. Погрешности вычислений. Любой численный результат на ЭВМ можно получить только с помощью конечной последовательности арифметических или логических операций. Ограниченность разрядной сетки ЭВМ и замена бесконечного сходящегося процесса конечным неизбежно приводит к возникновению погрешностей вычислений. Это вызывает необходимость анализа погрешностей и выполнения гарантированных оценок точности вычислений.

2. Анализ устойчивости вычислительного алгоритма и полученного с его использованием решения. В численных методах данная проблема имеет особое значение, так как связана с анализом критериев и условий роста погрешностей при реализации вычислительного алгоритма, а также с исследованием влияния погрешностей исходных данных на получаемое решение задачи.

3. Эффективность (экономичность) вычислительного алгоритма. Для практического применения алгоритма весьма важна его эффективность, которую иногда оценивают по количеству арифметических операций, необходимых для получения решения. Однако следует помнить, что часто уменьшение количества арифметических операций достигается в результате логического усложнения алгоритма. В результате, программы для логически усложненного алгоритма могут получаться столь неэкономичными, что весь выигрыш, достигнутый за счет снижения количества арифметических операций, может потеряться. Следует также отметить, что программы ЭВМ могут разрабатываться не для разового, а для многократного применения, поэтому наряду с эффективностью вычислительного алгоритма важна эффективность его реализации в программе.

Одним из важных вопросов численных методов является разработка вычислительного алгоритма, удовлетворяющего требованиям высокой точности, устойчивости и эффективности (экономичности).

По мнению авторов, в данном учебно-методическом пособии не целесообразно акцентировать внимание на вопросах организации вычислительных процессов, оценки и повышения качества программных алгоритмов, необходимости эффективной организации многократного решения задач, а также на целесообразности экономии вычислительных ресурсов ЭВМ.