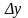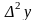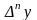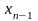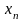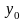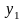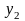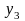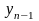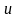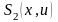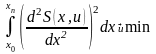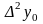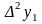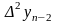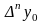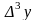- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
3.2.3. Полином Ньютона
Рассмотрим
регулярную интерполяционную сетку с
равноотстоящими узлами
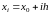 ,
,
где
– шаг интерполяции. Интерполянт будем
искать в следующем виде:
,
,
где
– шаг интерполяции. Интерполянт будем
искать в следующем виде:
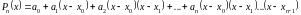 .
(3.14)
.
(3.14)
Составим таблицу
конечных разностей функции
(табл. 3.1), приняв обозначения:
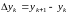 ,
,
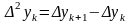 ,
…,
,
…,
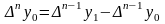 .
.
Конечной разностью
первого порядка
называют разность между двумя соседними
значениями функции
в узлах интерполяции. Конечной
разностью второго порядка
называют разность между двумя соседними
конечными разностями первого порядка.
В общем случае конечной
разностью порядка
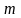 (для
(для
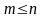 )
называют разность между двумя соседними
конечными разностями порядка
)
называют разность между двумя соседними
конечными разностями порядка
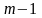 .
.
Таблица 3.1.
Конечные разности функции .
|
|
|
|
… |
|
…
|
…
|
…
|
…
|
… … … … … … … … |
|
Заметим, что для
любого многочлена степени
все конечные разности
равны между собой, а конечная разность
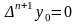 .
Значение
соответствует максимальному показателю
степени интерполяционного полинома
Ньютона. Можно показать, что для того
чтобы выполнялись условия интерполяции
.
Значение
соответствует максимальному показателю
степени интерполяционного полинома
Ньютона. Можно показать, что для того
чтобы выполнялись условия интерполяции
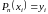 ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
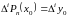 ,
или
,
или
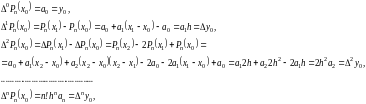
откуда нетрудно
получить формулы для вычисления
коэффициентов
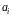 ,
:
,
:
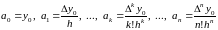 .
(3.15)
.
(3.15)
Подставив (3.15) в (3.14) получим
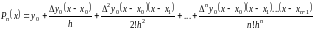 .
(3.16)
.
(3.16)
Рассмотрим
пример. Пусть
для известного заранее аналитического
вида функции
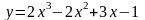 требуется построить таблицу конечных
разностей и в соответствии с ней
восстановить аналитический вид функции.
требуется построить таблицу конечных
разностей и в соответствии с ней
восстановить аналитический вид функции.
Решение. Пусть
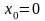 ,
,
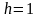 ,
а
,
а
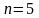 .
.
|
|
|
|
|
0 1 2 3 4 5 |
–1 2 13 44 107 214 |
3 11 31 63 107 |
8 20 32 44 |
12 12 12 |
Заметим, что конечные разности равны между собой, поэтому максимальный показатель степени искомого многочлена равен 3.
В соответствии с
(3.15) получим:
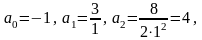
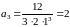 .
Подставив полученные значения в (3.16),
получим:
.
Подставив полученные значения в (3.16),
получим:
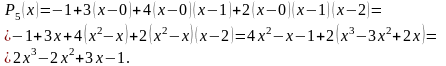
Полученный результат позволяет утверждать, что если бы аналитический вид рассматриваемой в данном примере функции был бы не известен, но была бы задана соответствующая таблица конечных разностей, то интерполяционная формула Ньютона позволила бы восстановить аналитический вид функции.
Выражение (3.16)
является первой интерполяционной
формулой Ньютона, которая при ручных
вычислениях применяется несколько в
ином виде. Положим
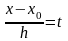 ,
то есть
,
то есть
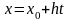 ,
тогда:
,
тогда:
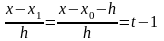 ,
,
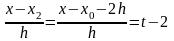 ,
,
…
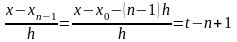 .
.
Подставляя данные выражения в (3.16), получаем:
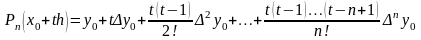 .
.
Данная формула
применяется в начале отрезка
интерполирования, когда значение
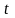 мало по абсолютной величине. Погрешность
полученной интерполяционной формулы
может быть вычислена по формуле:
мало по абсолютной величине. Погрешность
полученной интерполяционной формулы
может быть вычислена по формуле:
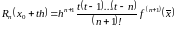 ,
,
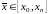 .
.
Погрешность можно оценить приближенно по следующей формуле:
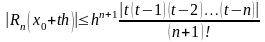 .
.
Интерполяционная формула Ньютона представляет собой один из способов составления интерполяционного многочлена, но используется только для регулярных интерполяционных сеток. Она полезна, поскольку число используемых узлов может быть легко увеличено или уменьшено без необходимоти повторного вычисления остальных коэффициентов полинома в формуле Ньютона.
Когда значение аргумента находится ближе к концу отрезка интерполяции, используется вторая интерполяционная формула Ньютона, которая получается, если искать интерполяционный полином в виде:
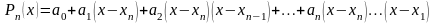 .
(*)
.
(*)
Коэффициенты полинома находятся из условия совпадения значений функции и интерполяционного многочлена в узлах интерполяции:
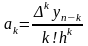 .
.
Подставив полученное
выражение в формулу полинома (*) и перейдя
к переменной
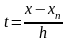 ,
получим окончательный вид интерполяционной
формулы Ньютона, используемой при ручных
вычислениях:
,
получим окончательный вид интерполяционной
формулы Ньютона, используемой при ручных
вычислениях:
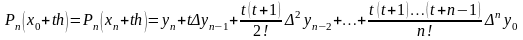 .
.
Погрешность второй интерполяционной формулы Ньютона можно приближенно оценить следующим образом:
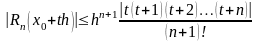 .
.