3.1.3. Экономизация степенных рядов

Полиномы Чебышева дают очень хорошее приближение функции, но эти приближения довольно сложно вычислять. Существует относительно простой метод корректировки традиционного разложения функции в степенной ряд (например, в ряд Тейлора) до разложения функции по полиномам Чебышева.

Пусть дана часть степенного ряда функции на отрезке [–1,1]:

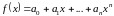. (3.6)

Используя представление полиномов Чебышева степеней 0, 1, 2, ..., можно вычислять функции 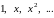в разложении по полиномам Чебышева:

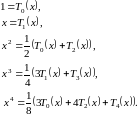(3.7)

Подстановка (3.7) в (3.6) преобразует разложение функции в степенной ряд (3.6) в ряд, разложенный по полиномам Чебышева:

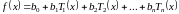. (3.8)

Для широкого класса функций их разложение по полиномам Чебышева сходится намного быстрее, следовательно, мы можем надеяться, что 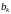, , в формуле (3.8) убывают гораздо быстрее, чем 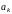, , в (3.6). Тогда, не уменьшая общую точность приближения функции (за счет улучшения структуры ее представления), можно понизить степень многочлена, удалив из (3.8) последний член разложения, если 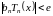, где – некоторая заданная точность. В результате, с помощью многочлена меньшей степени доступно вычисление функции без ущерба для точности ее представления в ЭВМ.

3.1.4. Приближения с помощью дробно-рациональных функций

Некоторые функции нельзя достаточно точно приблизить многочленами, например, имеющие асимптоты. Асимптотой графика функции называется такая прямая, расстояние от точки 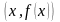до которой стремится к нулю при неограниченном удалении точки графика от начала координат.

Рациональные функции способствуют получению хороших приближений. Наиболее сложную проблему составляет вопрос выбора вида дробно-рациональной функции 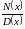для заданной функции , где 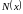и 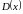– многочлены. При выборе вида рациональной функции следует учитывать всю имеющуюся априорную информацию: симметрию приближаемой функции, точки разрыва, нули функции и т.д. Проиллюстрируем идею метода на примере. Пусть рациональная функция является отношением двух полиномов третьего порядка:

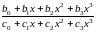. (3.9)

Для функции по формуле Тейлора получено разложение в ряд:

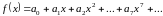. (3.10)

Приравнивая (3.9) и (3.10), а также приводя полученное равенство к общему знаменателю, получим

.

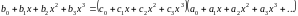Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях 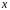, получаем систему уравнений, из которой определим коэффициенты

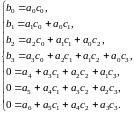
Последние три уравнения отражают тот факт, что в числителе рационального приближения коэффициенты многочлена при степенях выше третьей равны нулю. При использовании данного метода возникает ошибка 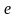, которую можно оценить следующим образом. Вычислим каким был бы коэффициент 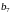, если бы он был включен в это приближение, и разделим его на величину знаменателя:

.

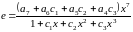Для повышения точности приближения функции рациональной функцией степенной ряд (3.10) целесообразно подвергнуть экономизации.

3.2. Методы интерполяции функций

Довольно часто информация о функции задана не аналитически, а в виде значений в конечном множестве ее узловых точек (дискретно). Для реализации вычислительных алгоритмов обычно требуется восстановить функцию с дискретного множества точек (заданную таблично) на непрерывную область ее определения. 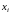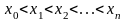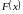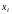Приближенная замена функции , заданной на множестве отдельных точек , (пусть ), функцией , значения которой в точках совпадают с соответствующими значениями функции , называется интерполяцией функции функцией . Точки называют узлами интерполяции, а – интерполянтом или интерполирующей функцией. При этом предполагается, что значения функции в узлах известны точно. Множество узлов интерполяции 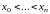называют интерполяционной сеткой.