
- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
3.1.1. Формула Тейлора, ряд Тейлора
Наиболее простым
и достаточно эффективным способом
приближения функций является использование
формулы Тейлора для их разложения в
степенной ряд. Пусть задана непрерывная
функция
,
имеющая непрерывные производные до
порядка
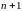 включительно. Такую функцию можно
разложить в некоторой окрестности точки
включительно. Такую функцию можно
разложить в некоторой окрестности точки
 по степеням
по степеням
 по формуле Тейлора:
по формуле Тейлора:
 ,
(3.1)
,
(3.1)
где
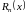 – остаточный член (ошибка, погрешность),
связанный с заменой при вычислении
бесконечного степенного ряда первыми
его
членами.
– остаточный член (ошибка, погрешность),
связанный с заменой при вычислении
бесконечного степенного ряда первыми
его
членами.
Ошибку ограничения
можно оценить по формуле,
где
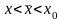 :
:
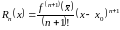 .
.
Формула Тейлора
не только дает возможность организовать
численный метод вычисления значений
функции
,
но и позволяет оценить величину ошибки
приближения, возникающей в результате
ограничения количества рассматриваемых
членов ряда. При ее использовании
требуется определить точку
 ,
в окрестностях которой будет производиться
разложение функции, при этом следует
руководствоваться соображениями
точности представления коэффициентов
ряда (3.1) и величиной используемого
интервала области определения, внутри
которого будут производиться вычисления.
,
в окрестностях которой будет производиться
разложение функции, при этом следует
руководствоваться соображениями
точности представления коэффициентов
ряда (3.1) и величиной используемого
интервала области определения, внутри
которого будут производиться вычисления.
Рассмотрим
разложение в ряд Тейлора функции
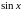 .
Найдем соответствующие производные и
в результате получим последовательность
функций:
.
Найдем соответствующие производные и
в результате получим последовательность
функций:
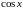 ,
,
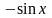 ,
,
 ,
,
,
,
,
,
… . Если положить
,
,
,
,
,
,
… . Если положить
 ,
то последовательность функций
преобразуется в ряд чисел 1, 0, –1, 0, 1, 0,
–1, 0, ..., тогда по формуле (3.1) мы имеем:
,
то последовательность функций
преобразуется в ряд чисел 1, 0, –1, 0, 1, 0,
–1, 0, ..., тогда по формуле (3.1) мы имеем:
 .
.
Оценим величину
ошибки приближения при рассмотрении
первых четырех членов ряда
 и
и
 ,
,
 ,
,
поскольку
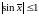 для любых
для любых
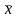 .
.
Из полученной оценки погрешности видно, что ошибка приближения зависит от и если не изменить число членов ряда в представлении функции , то для достаточно больших значение погрешности может превысить 1.
3.1.2. Полиномы Чебышева
Формула Тейлора
при разложении функции в степенной ряд
дает сходимость, зависящую от значения
.
Возникает идея поиска такого многочлена
 ,
чтобы максимальная ошибка приближения
функции
была бы наименьшей. Данная задача была
решена великим русским математиком
П.Л.Чебышевым и получила название задачи
о наилучшем приближении.
,
чтобы максимальная ошибка приближения
функции
была бы наименьшей. Данная задача была
решена великим русским математиком
П.Л.Чебышевым и получила название задачи
о наилучшем приближении.
Пусть задана
некоторая функция
,
которую на отрезке
требуется приблизить многочленом
 таким образом, чтобы
таким образом, чтобы
 ,
,
т.е. подобрать
такие коэффициенты
 ,
чтобы максимальная величина модуля
разности между
и
была наименьшей для любых
.
,
чтобы максимальная величина модуля
разности между
и
была наименьшей для любых
.
Определение.
Полиномом Чебышева называется многочлен
вида
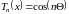 ,
где
,
где
 .
.
Заметим, что полиномы Чебышева не являются тригонометрическими функциями, однако доказательство данного утверждения приводить не будем. Используя известные формулы тригонометрии, найдем первые три многочлена:
 ,
,
 ,
,
 .
.
Для вычисления многочленов Чебышева практичнее использовать следующее рекуррентное соотношение:
 .
(3.2)
.
(3.2)
Свойства многочленов Чебышева:
Учитывая формулу (3.2), можно установить, что
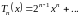 ,
,
 ,
то есть коэффициент
при старшей степени
многочлена Чебышева равен
,
то есть коэффициент
при старшей степени
многочлена Чебышева равен
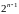 .
.Полиномы Чебышева
 образуют ортогональный базис (с весом
образуют ортогональный базис (с весом
 )
на множестве функций, непрерывных на
отрезке
)
на множестве функций, непрерывных на
отрезке
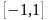 ,
и удовлетворяют следующим равенствам:
,
и удовлетворяют следующим равенствам:
 (3.3)
(3.3)
3. Многочлены Чебышева доставляют минимум максимальной ошибки приближения, то есть являются многочленами наилучшего приближения для класса функции, непрерывных на отрезке . Докажем данный факт.
Чебышев показал,
что точная верхняя грань (supremum,
супремум) многочлена
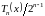 среди всех многочленов
среди всех многочленов
 с коэффициентом 1 при старшей степени
на отрезке
наименьшая. Действительно,
с коэффициентом 1 при старшей степени
на отрезке
наименьшая. Действительно,
 ,
откуда
,
откуда
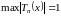 ,
тогда
,
тогда
 ,
причем экстремумы принимают попеременно
положительные и отрицательные значения
на отрезке [–1,1], так как
,
причем экстремумы принимают попеременно
положительные и отрицательные значения
на отрезке [–1,1], так как
 – гармоническая функция. Количество
экстремумов равно
– гармоническая функция. Количество
экстремумов равно
 .
Рассмотрим разность:
.
Рассмотрим разность:
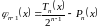 ,
которая является многочленом степени
,
которая является многочленом степени
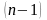 (поскольку члены
(поскольку члены
 уничтожаются). Если экстремальное
значение
меньше, чем у
,
то в
экстремальных точках полинома
уничтожаются). Если экстремальное
значение
меньше, чем у
,
то в
экстремальных точках полинома
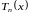 функция
функция
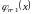 принимает по очереди положительные и
отрицательные значения. Следовательно,
имеет
действительных
корней, чего не тожет быть, так как
степень многочлена равна
.
Тогда выполняется тождество
принимает по очереди положительные и
отрицательные значения. Следовательно,
имеет
действительных
корней, чего не тожет быть, так как
степень многочлена равна
.
Тогда выполняется тождество
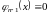 или
или
 .
.
Последнее свойство полиномов Чебышева представляет большой интерес для численного анализа. Если какая-либо ошибка приближения может быть выражена многочленом Чебышева степени , то любое другое выражение для ошибки в виде многочлена степени , имеющего тот же самый коэффициент при старшей степени , будет иметь на отрезке [–1,1] большую максимальную ошибку, чем чебышевское.
Практика
использования полиномов Чебышева для
решения задачи приближения функции
заключается в следующем. Поскольку
система функций
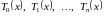 образует базис, то на отрезке [–1,1] любую
функцию можно представить как линейную
комбинацию
образует базис, то на отрезке [–1,1] любую
функцию можно представить как линейную
комбинацию
 ,
:
,
:
 .
(3.4)
.
(3.4)
Коэффициенты
разложения можно определить, используя
свойство ортогональности (3.3) полиномов
Чебышева. Для определения
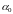 почленно умножим левую и правую часть
выражения (3.4) на
почленно умножим левую и правую часть
выражения (3.4) на
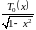 и проинтегрируем:
и проинтегрируем:
 .
.
Учитывая ортогональность, имеем:
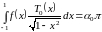 или
или
 .
.
Аналогично можно вычислить остальные коэффициенты разложения (3.4):
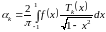 ,
.
(3.5)
,
.
(3.5)
Единственной проблемой разложения функции по полиномам Чебышева является вычисление достаточно сложных интегралов вида (3.5).
