2.4.2.5. Оценка надежности параметров множественной регрессии и корреляции

Оценка значимости множественного уравнения регрессии в целом проводится с помощью , (критерия Фишера).

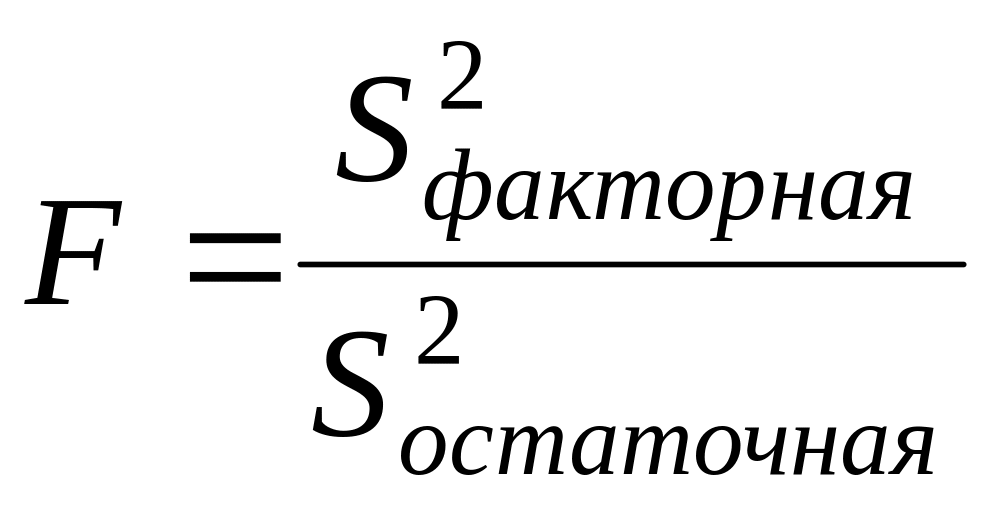(157)

где:

– факторная дисперсия (158)

– остаточная дисперсия (159)

F-критерий можно рассчитать и по формуле:

(160)

где:

- для линейной множественной модели – число факторов включенных в регрессионную модель. Для нелинейной модели - число параметров при и их линеаризации ( и так далее), которое может быть больше числа факторов

- число наблюдений

Если расчетный превышает табличный при определенном уровне значимости или , и числе свободы - , (таблицы Снедекора-Фишера – приложение 2) можно сказать, что уравнение множественной регрессии статистически значимо.

Величина позволяет также оценить статистическую значимость и коэффициента (индекса) множественной корреляции .

Кроме оценки уравнения в целом, большое практическое значение имеет статистическая оценка значимости каждого отдельно включенного в модель фактора, через частные критерии Фишера , ( ). Данная оценка позволяет оценить целесообразность включения в модель множественной регрессии каждого из факторов после введения в модель остальных факторов.

Расчет частного , для фактора проводится по формуле:

(161)

- коэффициент множественной детерминации для модели, включающей все факторы

- коэффициент множественной детерминации для модели, без включения фактора

Расчета частного в общем виде, для фактора проводится по формуле:

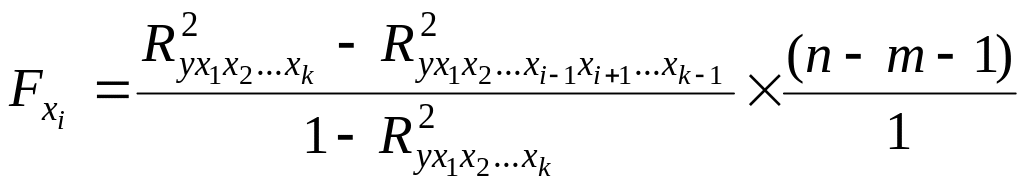(162)

Расчета частного , для оценки значимости влияния фактора после включения в модель других факторов проводится по формуле:

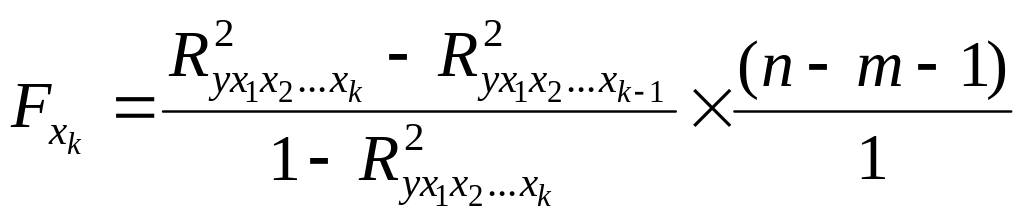(163)

Если величина расчетного частного превышает величину табличного при определенном уровне значимости или , и числе свободы - , (таблицы Снедекора-Фишера – приложение 2), можно сказать, что включение в модель фактора , после введения в модель остальных факторов, целесообразно. Если величина расчетного частного меньше табличного значения, можно сказать, что включение в модель фактора , после введения в модель остальных факторов, статистически неоправданно, и его необходимо исключить из рассматриваемой модели.

Зная величину частного критерия Фишера , рассчитывают частные критерии Стьюдента, для определения значимости каждого из коэффициентов чистой регрессии .

(164)

Критерий Стьюдента также можно рассчитать по формуле:

(165)

где:

- коэффициент чистой регрессии для фактора

- стандартная ошибка (166)

где:

- коэффициент детерминации множественного уравнения регрессии

- коэффициент множественной детерминации зависимости фактора со всеми остальными факторами уравнения множественной регрессии

- среднеквадратическое отклонение результативного признака

- среднеквадратическое отклонение факторного признака

Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости , или , и числе степеней свободы (приложение 1). Если фактическое значение больше табличного соответствующий коэффициент регрессии статистически значим.

Фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости , или , и числе степеней свободы , где - число исключенных переменных (приложение 1). Если фактическое значение больше табличного соответствующий коэффициент частной корреляции статистически значим.

Пример 22. По данным примеров 20 и 21 необходимо:

1. провести оценку существенности уравнения регрессии и его параметров:

2. рассчитать частные . Оценить с их помощью статистическую значимость включения факторов , , , решить вопрос включения в регрессионную модель одних факторов после включения других.

Решение.

1. Оценку существенности множественного уравнения проведем, используя критерий Фишера (F-критерий)

.

где:

– число факторов включенных в регрессионную модель.

– число наблюдений

Табличное значение для данной модели при уровне значимости , и числе свободы – , (значение 35 в приложении 2 отсутствует, возьмем ближайшее значение 30) будет равно 2,69.

Расчетное значение значительно больше табличного, соответственно множественное уравнение регрессии признается статистически значимым.

Расчет фактического , в программе Microsoft Excel – рисунок 9.

2. Рассчитаем частные для оценки значимости влияния фактора после включения в модель других факторов

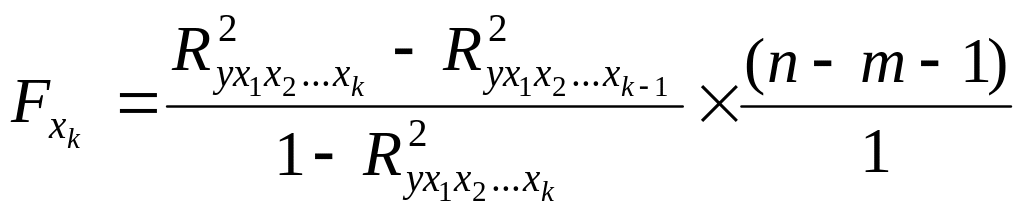
Табличное значение при уровне значимости , и числе свободы - , будет равно 4,12.

а)

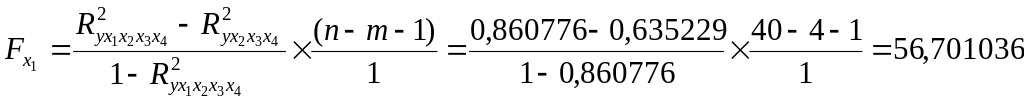
Фактическое значение больше табличного. Значит включение в модель фактора после факторов , , статистически значимо.

б)

Фактическое значение больше табличного. Значит включение в модель фактора после факторов , , статистически значимо.

в)

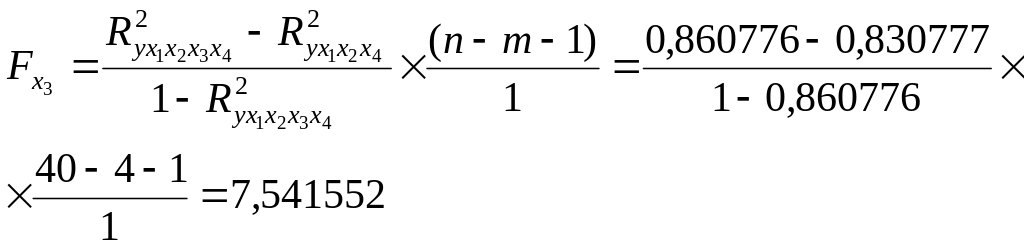
Фактическое значение больше табличного. Значит включение в модель фактора после факторов , , статистически значимо.

г)

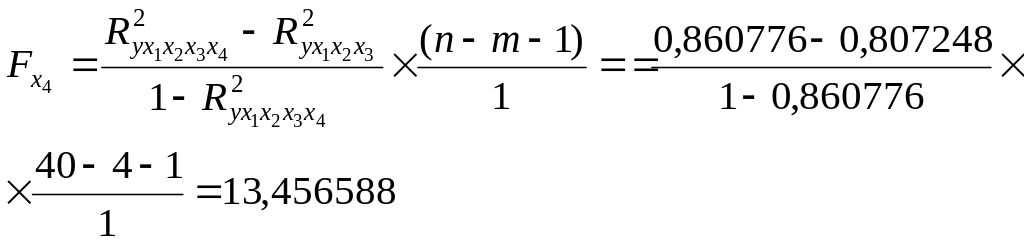
Фактическое значение больше табличного. Значит включение в модель фактора после факторов , , статистически значимо.

где: – коэффициент множественной детерминации для множественной регрессионной модели со всеми включенными в нее факторами.

– коэффициент множественной детерминации для множественной регрессионной модели без фактора .

– коэффициент множественной детерминации для множественной регрессионной модели без фактора .

– коэффициент множественной детерминации для множественной регрессионной модели без фактора .

– коэффициент множественной детерминации для множественной регрессионной модели без фактора .

Значения коэффициентов , , , , рассчитаем в программе Microsoft Excel, методика расчета рассмотрена в примере 20 рисунок 9.

3. Статистическую оценку значимости коэффициентов регрессии по Стьюдента. Зная частные воспользуемся следующей формулой:

а)

б)

в)

г)

Табличное значение критерия Стьюдента при , и числе степеней свободы (значение 35 в приложении 1 отсутствует, возьмем ближайшее значение 30) равно 2,0423. Все фактические значения критерия Стьюдента больше табличного, то есть можно сделать вывод о статистической значимости всех коэффициентов регрессии .

Расчет и критериев Стьюдента для в программе Microsoft Excel приведен на рисунке 9. обозначен как F, а критерии Стьюдента как t-статистика.