2.4.2. Множественная регрессия. Множественная Корреляция.

2.4.2.1. Множественная регрессия.

В тех случаях, когда известно, что на результативный признак существенное влияние оказывает не один, как в парной модели, а несколько факторов, причем их влиянием нельзя пренебречь рассчитывают функцию не парной, а множественной регрессии.

(115)

Множественная модель позволяет установить связь результативного признака с каждым отдельно взятым фактором, при условии неизменяемости других включенных в модель факторных признаков.

При построении функции множественной регрессии, как и в парной регрессии, необходимо решить две задачи:

1. отбор факторов,

2. спецификация модели.

Отбор факторов модели множественной регрессии

Так как, во множественной регрессии исследуют влияние на результат нескольких факторов, то в отличии от парной модели, имеются особые требования к их отбору.

1. Все факторы должны быть выражены в количественных единицах. Качественные факторы, при включении их в модель, необходимо перевести в количественные, например, путем пересчета в баллы.

2. Факторы, включенные в модель, не должны быть интеркоррелированы, то есть факторы во множественной модели не должны находится в сильной корреляционной связи между собой, сила связи между факторами не должна быть выше чем сила связи между каким то фактором и результатом. В статистике говорят, что факторы явно коррелированны, если коэффициент корреляции между ними , а если связь между ними близка к функциональной, то наличие такой связи называется мультиколлинеарностью.

Спецификация модели множественной регрессии

Функция множественной регрессии может, как и парной регрессии, иметь линейный или нелинейный вид.

Наиболее широкое распространение получила линейная функция:

(116)

Но при значительной вариации признаков возможно применение нелинейных функций. Данные функции, так же, как и в парной регрессии должны иметь возможность их линеаризации. Из всего множества нелинейных функций чаще всего используется:

1. Множественная степенная функция

(117)

2. Множественная показательная функция

(118)

3. Множественная экспонента

(119)

4. Множественная гипербола

(120)

5. Множественная парабола второго порядка

(121)

Выбор вида функции проводится аналитическим или экспериментальным методами.

Расчет параметров уравнения множественной регрессии

Параметры множественной регрессии, как и параметры парной регрессии можно определить, используя МНК. Так для расчета параметров уравнения множественной линейной регрессии:

МНК даст систему уравнений:

(122)

Параметры уравнения находим как отношение частных определителей к определителю системы

, , ,…, (123)

где

- определитель системы, находится, как:

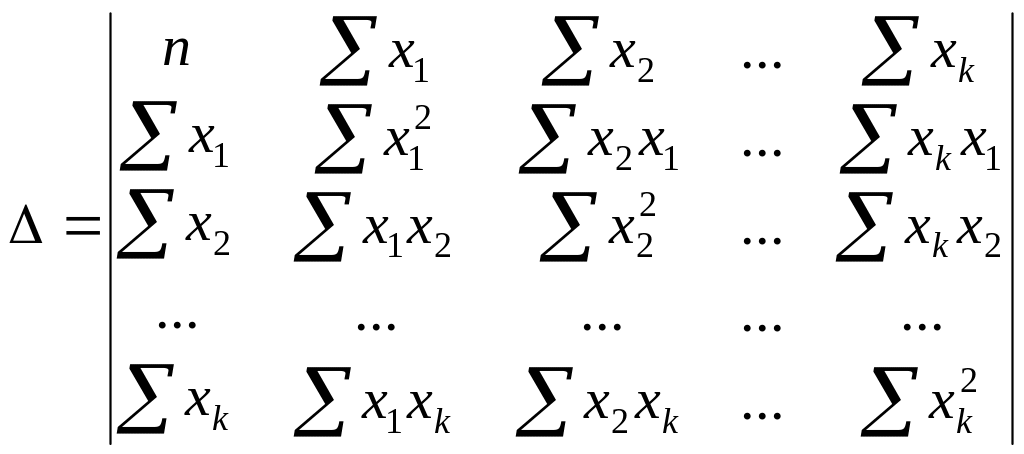(124)

- частные определители системы рассчитывают, заменяя соответствующий столбец матрицы определителя системы данными левой части системы.

Параметр во множественной регрессии называется свободным членом уравнения регрессии и также как в парной регрессии не имеет экономической интерпретации. Параметр - коэффициентом регрессии, он показывает, на сколько единиц, в среднем, изменится результативный признак , если соответствующий данному коэффициенту фактор увеличится на одну единицу при постоянной величине остальных факторов.

Коэффициенты регрессии можно рассчитать и используя уравнения регрессии в стандартизованном виде представив все переменные уравнения как центрированные и нормированные. Для этого выразим их как отношение их отклонений от средних величин на их стандартное отклонение:

(125)

где

- стандартизованные переменные:

(126)

(127)

- стандартизованные коэффициенты регрессии , показывают на сколько, в среднем, среднеквадратических отклонений изменится вариация результативного признака , если вариация соответствующего фактора увеличится на одно среднеквадратическое отклонение, при постоянной величине остальных факторов. Расчет параметров уравнения в стандартизированной форме более прост, так как, по сравнению с уравнением в натуральной форме отсутствует параметр .

МНК для уравнения множественной регрессии в стандартизированном масштабе даст следующую систему уравнений:

(128)

где

- коэффициент парной корреляции (38)

или (39)

Как, и в уравнении в натуральном масштабе параметры стандартизированного уравнения можно найти методом определителей:

(129)

где:

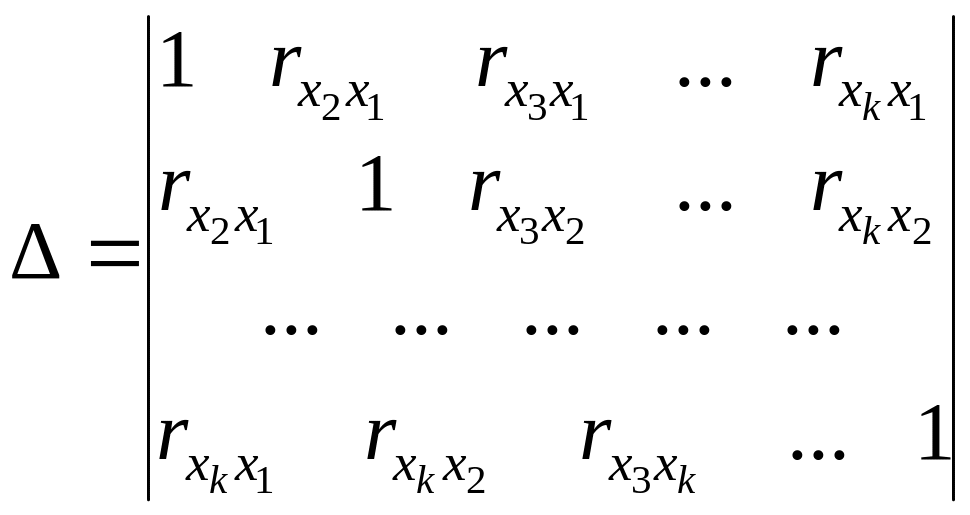(130)

Определитель получается из определителя , заменой в нем соответствующего столбца столбцом свободных членов исходной системы.

Кроме того, можно рассчитать используя их взаимосвязь с коэффициентами парной линейной корреляции. Так, например, для двухфакторной линейной модели, выраженной в стандартизованном масштабе, рассчитываются, как:

(131)

Определив значение -коэффициентов и зная, что между -коэффициентами и коэффициентами регрессии в натуральном масштабе существует следующая взаимосвязь:

или (132)

От уравнения множественной регрессии в стандартизованном виде

(125)

перейдем к уравнению в натуральном масштабе

(116)

параметр , который не рассчитали в стандартизованном уравнении, рассчитаем, как

(133)

Расчет параметров нелинейных уравнений множественной регрессии ведется так же, как и в линейной модели используя МНК. Разница заключается в том, что нелинейные модели вначале линеаризуются, и расчет параметров проводится по преобразованным данным (см. парную регрессию).