2.4.1.7. Оценка статистической надежности в парных нелинейных моделях
Как и в парной линейной регрессии, в регрессии нелинейной оценку надежности уравнения в целом проводят с помощью критерия Фишера (F-критерия), а оценку параметров уравнения и коэффициента детерминации проводят с помощью критерия Стьюдента.
Общая формула фактического F-критерия имеет вид;
(95)
где:
- индекс детерминации.
- число наблюдений.
- число параметров при переменных .
В случае нелинейной регрессии отлично для разных видов регрессии, и формула F-критерия различна для различных функций.
Например. Для
степенной
и показательной
и:
(96)
Для параболы
второго порядка
и:
(97)
Для параболы
третьего порядка
и:
(98)
Как и в случае
линейной регрессии, критерий Фишера
фактический сравнивают с критерием
Фишера табличным, при определенном
уровне значимости
или
,
и числе степеней свободы -
,
(таблицы Снедекора-Фишера – приложение
2).
Значимость параметров уравнения парной нелинейной регрессии и индекса корреляции проверяется, аналогично парной линейной регрессии, используя критерий Стьюдента.
Критерий Стьюдента для коэффициента регрессии рассчитывается как;
(51)
где; - коэффициент регрессии.
- стандартная ошибка коэффициента регрессии, рассчитывается как:
(52)
Учитывая, что
(53)
Критерий Стьюдента для параметра рассчитывается как;
(54)
где: - свободный член уравнения регрессии.
- стандартная ошибка параметра , рассчитывается как:
(55)
или (56)
Критерий Стьюдента
для индекса корреляции
рассчитывается как;
(57)
или
(58)
где: - индекс корреляции.
-
стандартная ошибка индекса корреляции,
рассчитывается как:
(59)
Качество подбора модели определяют, рассчитывая среднюю ошибку аппроксимации. Для расчета средней ошибки аппроксимации используют формулы:
(99)
(100)
где
(101)
(102)
Чем меньше средняя
ошибка аппроксимации, тем выше качество
модели. Допустимый предел
не более 10%.
Пример 18. Необходимо оценить существенность уравнения регрессии равносторонней гиперболы , при:
где: - индекс детерминации.
- число наблюдений.
Решение. Оценку существенности уравнения нелинейной регрессии проведем, используя критерий Фишера (F-критерий)
.
- число параметров при переменных .
Найдем критерий
Фишера табличный, при уровне значимости
,
и числе степеней свободы -
,
(таблицы Снедекора-Фишера – приложение
2) -
.
Так как уравнение регрессии признаем статистически значимым.
Пример 19. По данным примеров 7; 11; 12; 13; 14 рассчитаем средние ошибки аппроксимации для линейной функции, функции параболы второй степени, равносторонней гиперболы, степенной и показательной функций.
Решение. Для расчета средней ошибки аппроксимации используем формулу:
,
где
Расчет произведем в таблице 38. Средние ошибки аппроксимации составили для:
линейной функции
параболы второго порядка
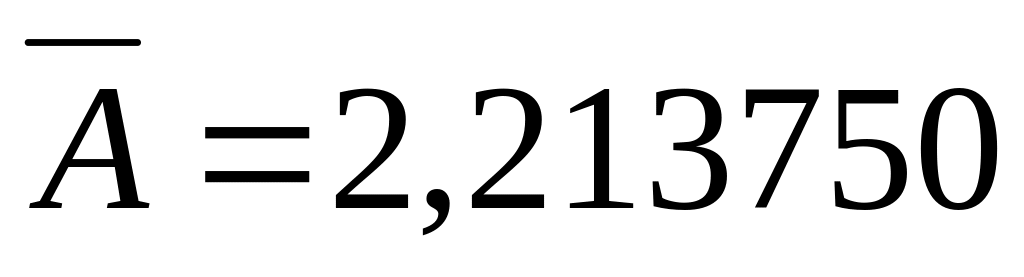
функции равносторонней гиперболы
степенной функции
показательной функции
Соответственно
линейная функция наиболее качественно
описывает существующую взаимосвязь
между исследуемыми явлениями. Но все
регрессии находятся в допустимых
пределах (
не более 10%).
Таблица 38
-
№
Линейная
Парабола второго порядка
Гипербола
1
37,8
37,792344
0,007656
0,020254
38,023560
0,223560
0,591429
36,808395
0,991605
2,623294
2
38,0
38,028410
0,028410
0,074763
38,158005
0,158005
0,415803
38,266516
0,266516
0,701358
3
39,0
38,264476
0,735524
1,885959
38,307508
0,692492
1,775621
38,891425
0,108575
0,278397
4
37,5
38,382510
0,882510
2,353360
38,387907
0,887907
2,367752
39,086709
1,586709
4,231224
5
39,5
38,500543
0,999457
2,530271
38,472071
1,027929
2,602352
39,238597
0,261403
0,661780
6
36,8
38,736609
1,936609
5,262524
38,651694
1,851694
5,031777
39,459524
2,659524
7,226967
7
40,0
38,972676
1,027324
2,568310
38,846375
1,153625
2,884063
39,612474
0,387526
0,968815
8
40,1
39,326775
0,773225
1,928242
39,166634
0,933366
2,327596
39,770204
0,329796
0,822434
9
40,0
39,444808
0,555192
1,387980
39,280917
0,719083
1,797708
39,810409
0,189591
0,473978
10
39,0
40,034974
1,034974
2,653779
39,908803
0,908803
2,330264
39,956611
0,956611
2,452849
11
38,0
40,389074
2,389074
6,287037
40,330713
2,330713
6,133455
40,016262
2,016262
5,305953
12
41,0
40,507107
0,492893
1,202178
40,478879
0,521121
1,271027
40,033086
0,966914
2,358327
13
41,6
40,625140
0,974860
2,343413
40,630810
0,969190
2,329784
40,048664
1,551336
3,729173
14
41,0
40,979240
0,020760
0,050634
41,109192
0,109192
0,266322
40,089168
0,910832
2,221541
15
41,9
41,215306
0,684694
1,634115
41,446938
0,453062
1,081294
40,111951
1,788049
4,267420
Итого
591,2
32,182820
33,206244
38,323509
В среднем
2,145521
2,213750
2,554901
Продолжение табл. 38
-
№
Степенная
Показательная
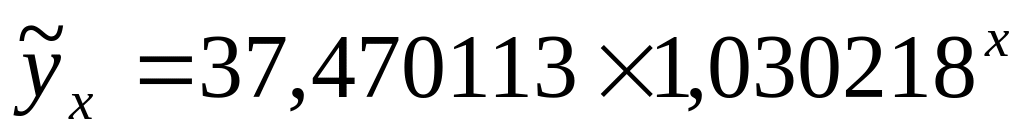
1
37,8
37,183851
0,616149
1,630024
37,806262
0,006262
0,016566
2
38,0
37,910774
0,089226
0,234805
38,032035
0,032035
0,084303
3
39,0
38,397333
0,602667
1,545300
38,259157
0,740843
1,899597
4
37,5
38,592153
1,092153
2,912408
38,373226
0,873226
2,328603
5
39,5
38,764817
0,735183
1,861223
38,487635
1,012365
2,562949
6
36,8
39,060772
2,260772
6,143402
38,717477
1,917477
5,210535
7
40,0
39,308870
0,691130
1,727825
38,948692
1,051308
2,628270
8
40,1
39,619441
0,480559
1,198401
39,298106
0,801894
1,999736
9
40,0
39,710581
0,289419
0,723548
39,415272
0,584728
1,461820
10
39,0
40,100534
1,100534
2,821882
40,006365
1,006365
2,580423
11
38,0
40,295293
2,295293
6,040245
40,365268
2,365268
6,224389
12
41,0
40,355237
0,644763
1,572593
40,485616
0,514384
1,254595
13
41,6
40,413002
1,186998
2,853361
40,606323
0,993677
2,388647
14
41,0
40,574705
0,425295
1,037305
40,970608
0,029392
0,071688
15
41,9
40,674075
1,225925
2,925835
41,215278
0,684722
1,634181
Итого
591,2
35,228156
590,987320
32,346303
В среднем
2,348544
2,156420