2.4.1.6. Парная нелинейная корреляция. В нелинейных моделях для определения силы связи рассчитывают индекс корреляции:

(92)

где;

- остаточная дисперсия результативного признака.

- общая дисперсия результативного признака.

Отсюда: 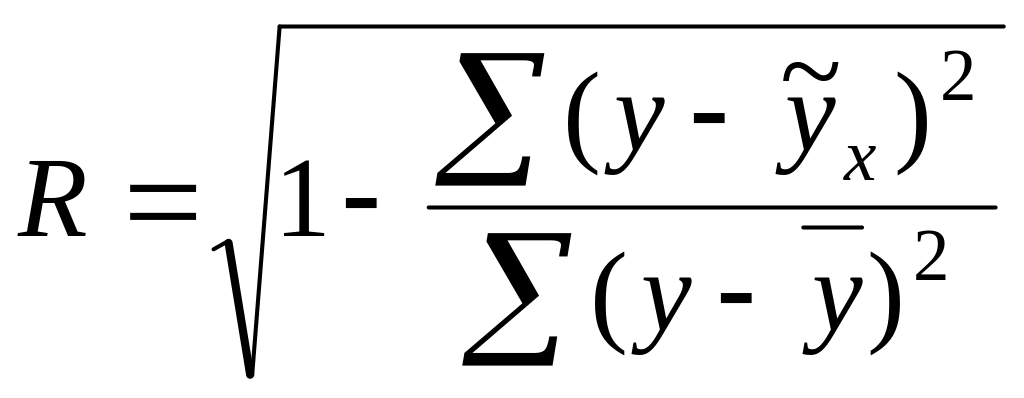(93)

Величина индекса корреляции может принимать значения от до , то есть, он показывает только тесноту связи, но не показывает ее направление.

Квадрат индекса корреляции – индекс детерминации характеризует долю вариации результативного признака обусловленную влиянием включенного в модель фактора .

(94)

Величина индекса детерминации определяет качество подбора функции регрессии, чем индекс детерминации выше, тем «лучше» выбор формы уравнения регрессии.

Пример 17. По данным примера 12 (функция регрессии равносторонней гиперболы ) рассчитать индекс корреляции, (табл. 37).

Решение.

1. Рассчитаем индекс корреляции

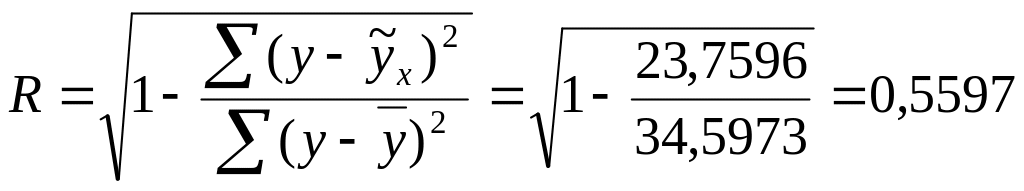
Индекс множественной корреляции показывает, что между исследуемыми явлениями существует средняя связь.

Таблица 37

№
1	37,80	36,808395	-1,6133	2,6027	0,9602	0,9220
2	38,00	38,266516	-1,4133	1,9974	-0,2770	0,0767
3	39,00	38,891425	-0,4133	0,1708	0,1071	0,0115
4	37,50	39,086709	0,0867	0,0075	0,2649	0,0702
5	39,50	39,238597	-1,9133	3,6607	-1,6938	2,8690
6	36,80	39,459524	-2,6133	6,8293	-2,6529	7,0379
7	40,00	39,612474	0,5867	0,3442	0,3964	0,1571
8	40,10	39,770204	0,6867	0,4716	0,3409	0,1162
9	40,00	39,810409	0,5867	0,3442	0,2013	0,0405
10	39,00	39,956611	-0,4133	0,1708	-0,9428	0,8889
11	38,00	40,016262	-1,4133	1,9974	-2,0016	4,0064
12	41,00	40,033086	1,5867	2,5176	0,9984	0,9968
13	41,60	40,048664	2,1867	4,7817	1,5664	2,4536
14	41,00	40,089168	1,5867	2,5176	0,9265	0,8584
15	41,90	40,111951	2,4867	6,1837	1,8040	3,2544
Сумма	591,2000			34,5973		23,7596
В среднем	39,4133

Рассчитаем индекс детерминации

Индекс детерминации показывает, что вариация результативного признака на 31% обусловлена влиянием включенного в модель фактора.