Линеаризация степенной функции
(72)
проводят путем логарифмирования обеих частей уравнения, получая уравнение вида:
(73)
Обозначив через
,
получим линейное уравнение регрессии:
(74)
МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:
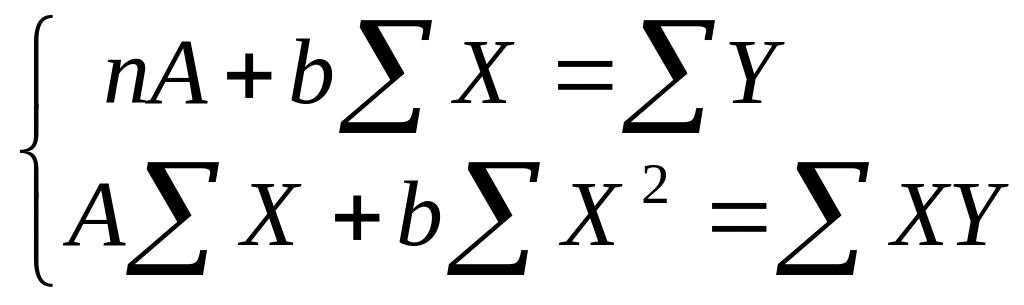(75)
Также можно использовать уравнения:
(76)
(77)
Рассчитав параметры
,
и составив линейное уравнение регрессии
необходимо провести его потенцирование,
чтобы вернуться к степенной функции.
(78)
Пример 13.
Имеются данные о средней прибыли
(млн.
руб.) и затратах на рекламу
(млн.
руб.) за декаду, по выборке, равной 15-ти
предприятиям сферы торговли. Рассчитать
степенную функцию
Таблица 31.
-
№
1
37,8
0,3
2
38,0
0,5
3
39,0
0,7
4
37,5
0,8
5
39,5
0,9
6
36,8
1,1
7
40,0
1,3
8
40,1
1,6
9
40,0
1,7
10
39,0
2,2
11
38,0
2,5
12
41,0
2,6
13
41,6
2,7
14
41,0
3,0
15
41,9
3,2
Решение. Для расчета параметров данной функции проведем ее линеаризацию, прологарифмировав обе части уравнения
Обозначив через , получим линейное уравнение регрессии:
МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:
В таблице 32 рассчитаем все возможные значения:
Таблица 32
№ |
|
|
|
|
|
|
1 |
37,80 |
0,30 |
1,577492 |
-0,522879 |
-0,824837 |
37,183851 |
2 |
38,00 |
0,50 |
1,579784 |
-0,301030 |
-0,475562 |
37,910774 |
3 |
39,00 |
0,70 |
1,591065 |
-0,154902 |
-0,246459 |
38,397333 |
4 |
37,50 |
0,80 |
1,574031 |
-0,096910 |
-0,152539 |
38,592153 |
5 |
39,50 |
0,90 |
1,596597 |
-0,045757 |
-0,073056 |
38,764817 |
6 |
36,80 |
1,10 |
1,565848 |
0,041393 |
0,064815 |
39,060772 |
7 |
40,00 |
1,30 |
1,602060 |
0,113943 |
0,182544 |
39,308870 |
8 |
40,10 |
1,60 |
1,603144 |
0,204120 |
0,327234 |
39,619441 |
9 |
40,00 |
1,70 |
1,602060 |
0,230449 |
0,369193 |
39,710581 |
10 |
39,00 |
2,20 |
1,591065 |
0,342423 |
0,544817 |
40,100534 |
11 |
38,00 |
2,50 |
1,579784 |
0,397940 |
0,628659 |
40,295293 |
12 |
41,00 |
2,60 |
1,612784 |
0,414973 |
0,669262 |
40,355237 |
13 |
41,60 |
2,70 |
1,619093 |
0,431364 |
0,698418 |
40,413002 |
14 |
41,00 |
3,00 |
1,612784 |
0,477121 |
0,769493 |
40,574705 |
15 |
41,90 |
3,20 |
1,622214 |
0,505150 |
0,819461 |
40,674075 |
Итого |
591,20 |
25,10 |
23,929804 |
2,037398 |
3,301443 |
590,961438 |
В среднем |
|
|
1,595320 |
0,135827 |
0,220096 |
|
|
|
|
|
0,089930 |
|
|
Подставим полученные значения в уравнение
Выполним потенцирование полученного уравнения
Подставляя в полученное уравнение значение фактора , рассчитаем .