2.4.1.2. Парная линейная корреляция
Простейшим методом определения наличия и формы взаимосвязи является построения корреляционной таблицы и графика «корреляционное поле».
Корреляционная таблица – таблица, в которой записываются частоты сочетаний результативного и факторного показателей. В настоящее время корреляционная таблица не используется для вычисления уравнения связи.
Пример 8. Имеются данные о себестоимости единицы продукции (руб.) и затратах на рекламу (млн. руб.) (табл. 23).
Таблица 23.
|
210 |
210 |
220 |
200 |
240 |
200 |
210 |
220 |
210 |
220 |
240 |
200 |
|
30 |
50 |
50 |
40 |
70 |
30 |
40 |
70 |
30 |
60 |
60 |
30 |
Составим корреляционную таблицу (табл. 24).
Таблица 24.
y x |
200 |
210 |
220 |
240 |
Итого |
30 |
2 |
2 |
|
|
4 |
240 |
1 |
1 |
|
|
2 |
50 |
|
1 |
1 |
|
2 |
60 |
|
|
1 |
1 |
2 |
70 |
|
|
1 |
1 |
2 |
Итого |
3 |
4 |
3 |
2 |
12 |
По корреляционной таблице можно сделать следующие выводы. Если и распложены по возрастанию, то расположение частот около диагонали таблицы слева вниз направо говорит о прямой форме связи, если по диагонали вверх направо, то связь обратная. Если частоты находятся равномерно по всей таблицы – связь слабая.
Корреляционное поле (графический метод изучения взаимосвязей) – точечный график, характеризующий единицу наблюдения по двум признакам. Факторный признак откладывается по оси абсцисс, результативный признак по оси ординат.
По данным примера 8 построим корреляционное поле (рис. 4).
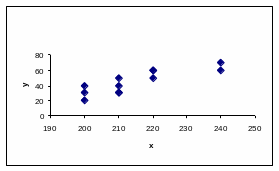
Рисунок 4
Анализ корреляционного поля показывает, что имеется прямая связь.
Если связь между признаками обратная, то корреляционное поле будет иметь примерно такой вид (рис. 5).
Рисунок 5
Если корреляционное поле имеет следующий вид (рис. 6) можно сделать вывод об отсутствии выраженной взаимосвязи.
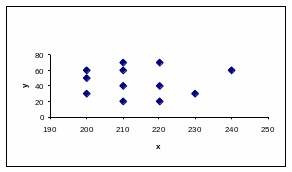
Рисунок 6
Корреляционная таблица и корреляционное поле показывают лишь наличие, отсутствие и направление связи. Но они не дают представления о тесноте, интенсивности связи между признаками.
Тесноту связи в
парной линейной модели определяют,
рассчитывая линейный
коэффициент парной корреляции
или просто коэффициент корреляции.
Существуют формулы расчета:
(38)
или
(39)
где: - коэффициент регрессии;
-
среднее квадратическое значение
факторного признака;
-
среднее квадратическое значение
результативного признака;
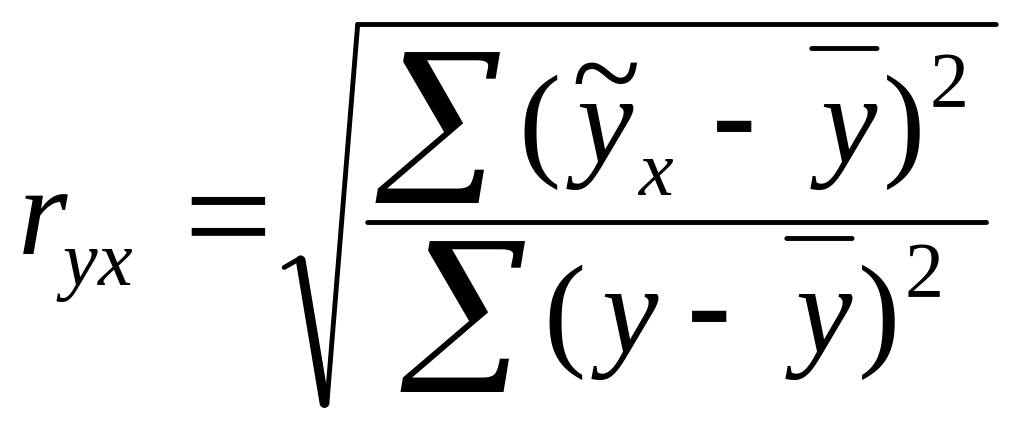(40)
где
-
сумма квадратов отклонений обусловленная
влиянием фактора
;
-
общая сумма квадратов отклонений
признака
.
Коэффициент корреляции также можно рассчитать через значение признаков в стандартизованном масштабе:
(41)
где:
– значения признаков в стандартизованном
масштабе.
(42)
(43)
Коэффициент корреляции может принимать значения от до . В статистике говорят, что если значения коэффициента парной корреляции:
меньше 0,3 (-0,3) связь положительная (отрицательная) слабая;
от 0,3 до 0,7 (от -0,3 до -0,7) связь положительная (отрицательная) средняя;
свыше 0,7 (-0,7) связь положительная (отрицательная) сильная;
равен 1 (-1) связь функциональная положительная (отрицательная);
равен 0 – связь отсутствует.
Другой
показатель тесноты связи – коэффициент
парной детерминации.
Он показывает часть вариации результативного
признака, которая сложилась под влиянием
включенного в парную модель фактора.
Коэффициент парной детерминации
рассчитывают, возводя в квадрат
коэффициент парной корреляции
или по формуле:
(44)
Коэффициент парной детерминации позволяет определять тесноту связи не только в линейных, но и в нелинейных моделях.
Коэффициент парной детерминации может принимать значения от до .
Пример 9. Имеются данные о средней прибыли (млн. руб.) и затратах на рекламу (млн. руб.) за декаду, по выборке, равной 15-ти предприятий сферы торговли (табл. 25).
Таблица 25.
№ |
|
|
1 |
37,80 |
0,30 |
2 |
38,00 |
0,50 |
3 |
39,00 |
0,70 |
4 |
37,50 |
0,80 |
5 |
39,50 |
0,90 |
6 |
36,80 |
1,10 |
7 |
40,00 |
1,30 |
8 |
40,10 |
1,60 |
9 |
40,00 |
1,70 |
10 |
39,00 |
2,20 |
11 |
38,00 |
2,50 |
12 |
41,00 |
2,60 |
13 |
41,60 |
2,70 |
14 |
41,00 |
3,00 |
15 |
41,90 |
3,20 |
Сумма |
591,20 |
25,10 |
В среднем |
39,413333 |
1,673333 |
|
1,518713 |
0,931283 |
Рассчитать
коэффициент парной линейной корреляции
и коэффициент парной линейной регрессии
.
Решение.
1) Так, как из примера 7 известно, что уравнение регрессии используем формулу:
Коэффициент
парной корреляции
показывает, что между исследуемыми
признаками существует тесная положительная
связь.
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации.
Коэффициент детерминации показывает, что 52% от всей вариации результативного признака обусловлено влиянием включенного в модель фактора, а 48% вариации вызвано влиянием всех остальных, не исследуемых в данной модели факторами.
2) Рассмотрим решение данной задачи в Microsoft Excel.
В новой книге Microsoft Excel внесем исходные данные (рис 7).
Далее нажимаем кнопку Сервис и в открывшийся панели нажимаем кнопку Анализ данных
В панели Анализ данных нажимаем корреляция:
В панели корреляция вводим входной интервал, выделяя все столбики, содержащий и данные результативного признака и данные фактора. Ответ можно поместить на новом рабочем листе, в новой рабочей книге, или на листе, содержащем условия выбирая выходной интервал, для чего указываем графа-клетку начала размещения ответа (рис. 7).
Рисунок 7.
Нажимаем ОК.
Появится таблица парных линейных коэффициентов корреляции (рис. 8).
Рисунок 8.
На пересечении столбца 1 и столбца 2 и будет искомый коэффициент парной линейной корреляции.