Методика решения задач по оптике для студентов инженерных специальностей
.pdf
|
4*. |
Составим полную систему уравнений для нахождения |
||||||
искомой величины λ : |
ϕ = (n −1)θ , |
|
|
|
||||
|
|
|
(1) |
|
|
|
||
|
|
|
|
|
L λ, |
|
|
|
|
|
|
(2) |
x = |
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
(3) |
L = a + b, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 = atgϕ, |
ϕ ≈ tgϕ. |
|
||
|
|
|
(4) |
|
||||
|
Система |
четырех |
уравнений (1) – (4) замкнута, так как |
|||||
содержит четыре неизвестные величины: ϕ, L, |
d, λ . |
|||||||
9*. Ответ: |
λ ≈ 5,2 10−7м = 520 нм. |
|
|
|||||
|
|
|
|
*************** |
|
|
||
|
|
|
|
Задача191 |
|
|
||
Луч |
света |
выходит |
под |
углом |
α = 32o |
из |
трехгранной |
|
равнобедренной призмы, показатель преломления вещества |
||||||||
которой n =1,6. Преломляющий угол призмы β = 35o. Найти |
||||||||
угол ε падения луча. |
|
|
|
|
|
|||
1*. Дано: |
|
|
Решение. |
|
|
|||
α = 32o, |
|
|
2*. |
|
N |
|
|
|
|
|
|
|
|
. |
|
|
|
n =1,6, |
|
|
|
|
β |
|
|
|
|
|
|
|
|
ϕ |
|
||
β = 35o. |
|
|
|
.C |
|
|
||
|
|
|
|
|
B |
D |
|
|
|
|
|
|
ε |
|
|
||
|
|
|
|
. γ |
θ |
. α |
|
|
|
|
|
|
|
|
|||
ε– ? |
|
|
|
|
. β |
|
|
|
|
|
|
|
K |
|
|
||
|
|
|
Q . |
|
|
n |
|
.M |
|
|
|
|
|
|
|
||
4*. |
Составим полную |
систему уравнений |
для |
нахождения |
||||
искомой величины ε: |
|
|
|
|
|
|||
|
|
|
|
|
|
- 270 - |
|
|
9*. Ответ: |
I3 ≈ 2,2 10−3 |
Дж |
= |
2,2 мДж . |
|
|
|||||||
|
|
|
|
м2 |
с |
|
|
м2 с |
|
|
|||
|
|
*************** |
|
|
|
|
|||||||
|
|
|
Задача193 |
|
|
|
|
|
|||||
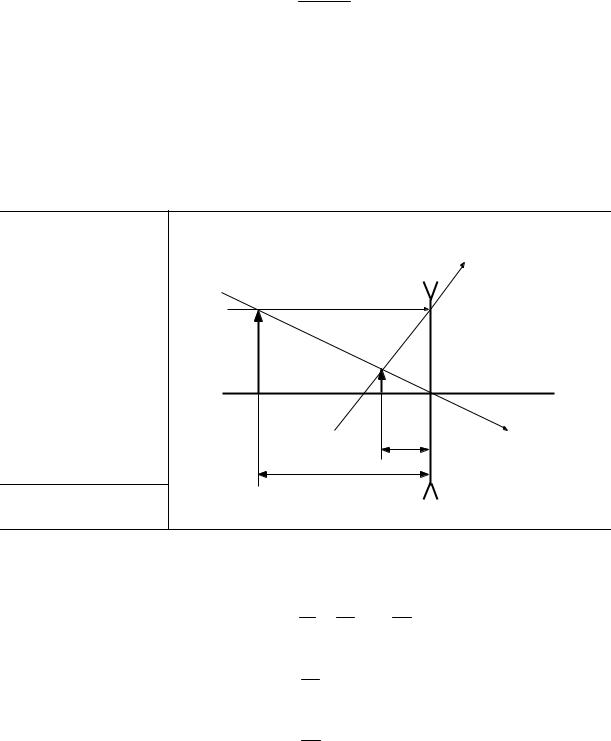
На каком расстоянии L от рассеивающей линзы, имеющей |
|||||||||||||
абсолютную |
величину |
оптической |
|
силы |
D = 4 |
дп, |
надо |
||||||
поместить предмет, чтобы его мнимое изображение получилось |
|||||||||||||
в θ = 5 раз меньше самого предмета? |
|
|
|
|
|
|
|||||||
1*. Дано: |
2 *. |
|
|
Решение. |
|
|
|
||||||
D = 4 дп, |
|
|
|
|
|
|
|
|
|
|
|||
θ = 5. |
|
|
.B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
A. . |
|
|
. |
. |
|
.C |
. |
|
|
||
|
|
|
|
. |
|
|
|
||||||
|
|
|
2F |
|
|
F |
A' |
|
F |
|
|
||
|
|
|
|
L |
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L– ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
4*. |
Составим |
полную |
систему |
уравнений |
для |
нахождения |
|||||||
искомой величины L: |
|
1 |
|
1 |
|
|
1 |
|
|
|
|
||
|
|
|
|
− |
= − |
, |
|
|
|
||||
|
|
(1) |
L |
f |
F |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
θ, |
|
|
|
|
|
|
||
|
|
(2) |
f |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= |
D. |
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|||||
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
Система |
трех уравнений (1) – (3) замкнута, так как |
||||||||||||
содержит три неизвестные величины: L, |
f , |
F . |
|
|
|
||||||||
9*. Ответ: |
|
L = 1,0 м. |
|
|
|
|
|
|
|
||||
|
|
*************** |
|
|
|
|
|||||||
|
|
|
|
|
|
|
- 272 - |
|
|
|
|
||
Задача194
Параллельный пучок света падает на стекло, показатель преломления которого неизвестен, а угол Брюстера αбр = 60o. Определить предельный угол αпред полного внутреннего отражения при прохождении такого пучка из стекла в воздух.
1*. Дано: |
π |
|
* |
Решение. |
||
o |
= |
рад. |
|
|
||
αбр = 60 |
3 |
2. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
n в=1 |
αбр |
ε |
|
|
|
|
n ст |
|
π/2 |
|
|
|
|
|
αпред |
|
|
|
|
|
пограничный луч |
||
|
|
|
|
γ |
||
αпред– ? |
|
|
|
|
|
|
4*. Составим полную систему уравнений для нахождения искомой величины αпред:
(1) |
tgαбр = nст, |
|
||
|
|
1 |
|
|
|
|
|
||
(2) |
sinαпред = |
|
. |
|
nст |
||||
|
|
|
||
Система двух уравнений (1) – (2) замкнута, так как содержит две неизвестные величины: nст, αпред .
9*. Ответ: αпред ≈ 6,2 10−1 рад ≈ 35,5o.
***************
Задача195
Точечный источник света находится на главной оси выпуклого зеркала радиусом r = 100 см на расстоянии d = 30 см от него. На расстоянии L = 2 м от зеркала находится экран. Чему равна
освещенность |
E |
экрана в точке, удаленной на расстояние |
S = 20 cм от |
оси |
зеркала, если сила света источника равна |
I = 200 кд? |
|
|
|
|
- 273 - |
9*. Ответ: |
E ≈ 1,1 102 лк = 110 лк. |
|
|
|
||||
|
|
*************** |
|
|
|
|
||
|
|
|
Задача196 |
|
|
|
|
|
Установка для получения колец Ньютона освещается |
||||||||
монохроматическим светом, падающим по нормали к |
||||||||
поверхности |
пластинки. |
Радиус кривизны линзы |
R = 12 м. |
|||||
Наблюдение ведется в отраженном свете. Сумма радиусов |
||||||||
колец Ньютона, соответствующих порядкам m = 5 |
и k = 25, |
|||||||
равняется |
L = 22,45 мм. |
Найти |
длину |
волны |
λ |
|||
монохроматического света. |
|
|
|
|
|
|||
1*. Дано: |
|
|
|
Решение. |
rk |
|
|
|
R = 12 м, |
|
|
rm |
|
|
|
||
|
|
|
|
|
|
|
|
|
m = 5, |
|
|
|
|
|
|
|
|
k = 25, |
|
|
|
|
|
|
|
|
L = 22,45 м = 2,245 10-2 м. |
|
|
|
|
|
|||
λ– ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
4*. |
Составим |
полную систему уравнений для нахождения |
||||||
искомой величины λ: |
|
Rλ(2m −1), |
|
|
|
|||
|
|
(1) |
rm = |
|
|
|
||
|
|
|
rk = |
Rλ(2k −1), |
|
|
|
|
|
|
(2) |
|
|
|
|||
|
|
(3) |
L = r |
+ r . |
|
|
|
|
|
|
|
k |
m |
|
|
|
|
Система |
трех уравнений (1) – (3) замкнута, так как |
|||||||
содержит три неизвестные величины: rm , |
rk , λ . |
|
|
|
||||
9*. Ответ: |
λ ≈ 4,2 10−7 м = 420 нм. |
|
|
|
||||
|
|
*************** |
|
|
|
|
||
|
|
|
- 275 - |
|
|
|
|
|
Задача197
Найти фокусное расстояние Fвд двояковыпуклой стеклянной
линзы ( ncт = 1,55 ), |
погруженной |
в |
воду |
|
|
( nв = 1,33), |
если |
|||||||||||||||||||||||
известно, что ее фокусное расстояние в воздухе Fвз = 20 см. |
||||||||||||||||||||||||||||||
1*. Дано: |
|
|
2* ─── |
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ncт = 1,55 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4*. |
Составим |
|
|
|
полную |
систему |
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
nв = 1,33, |
|
|
уравнений |
для |
нахождения |
искомой |
||||||||||||||||||||||||
F = 20 см = 2 10-1м. |
|
величины Fвд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
||||||||||||||
вз |
|
|
|
|
ст |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(1) |
|
R |
+ R |
|
= F |
, |
|
|||||||||||||||||||||
|
|
|
|
n |
−1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
в |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
вд |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
(2) |
nст |
−1 |
|
+ |
|
|
|
= |
|
, |
|
||||||||||||||||
|
|
|
|
|
|
R |
|
|
F |
|
||||||||||||||||||||
|
|
|
|
n |
|
R |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
вз |
|
1 |
|
|
2 |
|
|
|
|
вз |
|
|
|
|||||||||||||
Fвд– ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nвз = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Система |
трех |
|
уравнений |
(1) – (3) |
|
|
замкнута, |
|
так |
|
как |
|
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nвз. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
R + |
|
R |
|
|
|
|
|
||||||||||||||||
содержит три неизвестные величины: Fвд, |
|
, |
|
|
|
|||||||||||||||||||||||||
9*. Ответ: |
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Fвд ≈ 6,7 10−1м = 67 см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
*************** |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача198
Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отраженном
свете. Расстояние между m1 = 2 и k1 = 25 |
темными кольцами |
L1 = 4,8 мм. Найти расстояние L2 между |
m2 = 3 и k2 =16 |
темными кольцами Ньютона. |
|
- 276 -
спектр нулевого порядка, остальные спектры показаны условно.
действительного изображения будет минимальным, если |
||||||
оптическая сила такой линзы |
D = 25 дп. |
|
||||
1*. Дано: |
2*. |
|
Решение. |
|
||
D = 25 дп. |
|
|
|
|
||
|
|
B |
|
|
|
экран |
|
|
. |
F. |
F . |
|
|
|
|
2F |
F |
2F |
||
|
|
A. . |
. |
A'. . |
||
|
|
|
|
|
|
B' |
|
|
|
|
L |
|
. |
|
|
|
|
|
|
|
|
|
|
S |
|
f |
|
f – ? |
|
S + f = Lmin |
D = 1/F |
|
||
|
|
|
|
|
|
|
4*. |
Составим полную систему уравнений для нахождения |
|||||
искомой величины f : |
|
|
|
|
||
|
1 |
|
|
|
1 |
|
|
1 |
|
||
(1) |
|
|
|
+ |
|
|
|
= |
|
, |
|
|
|
S |
|
f |
F |
||||||
|
|
|
|
|
|
|
|
||||
|
|
L = S + f , |
|
||||||||
(2) |
|
|
|
||||||||
|
|
|
dL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f = корень (3) |
||
(3) |
|
|
= 0, |
|
|||||||
|
|
|
|
||||||||
|
|
|
df |
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
F = |
|
|
|
|
|||||
(4) |
|
|
|
. |
|
|
|||||
|
D |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
Система |
четырех |
уравнений (1) – (4) замкнута, так как |
|||||||||
содержит четыре неизвестные величины: S, f , L, F . |
|||||||||||
9*. Ответ: |
|
|
|
|
f |
= 8,0 10−2м = 80 мм. |
|||||
|
|
|
|
|
|
|
|
|
*************** |
||
Задача200
Два николя расположены так, что угол между их главными плоскостями равен ψ = π
6. Определить, во сколько раз θ
интенсивность естественного света больше интенсивности луча на выходе из второго николя, если суммарные потери на отражение и поглощение в каждом кристалле составляли k = 11%.
- 278 -
1*. Дано: |
|
Решение. |
|
|
|
ψ = π 6, |
2* . |
|
|
A1 |
|
|
|
|
|
|
|
k = 11%. |
I0 |
|
I1e |
o |
I2e |
|
B |
|
e |
||
|
|
e |
B1 |
|
|
|
|
|
|
|
|
θ– ? |
o |
|
|
|
|
A |
|
B |
B1 |
|
|
|
|
|
|
|
|
|
оптические |
|
ψ |
|
|
|
|
A A1 |
|
|
|
|
оси |
|
|
|
|
4*. Составим полную систему уравнений для нахождения искомой величины θ:
|
I1e = |
1 |
|
− |
k |
|
|
|
|
(1) |
2 |
I0 1 |
100 |
, |
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
k |
|
|
|
I2e = I1e cos |
2 |
|
− |
|
||||
(2) |
|
ψ 1 |
100 |
, |
|||||
|
|
|
|
|
|
|
|
|
|
θ = I0 |
I2e . |
|
|
|
|
|
|
||
(3) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система трех уравнений (1) – (3) не замкнута, так как содержит четыре неизвестные величины: I0 , I1e , I2e , θ . Однако
уравнения (1) – (3) линейно зависимы относительно переменных I0 , I1e , I2e . Решение системы получается последовательной
подстановкой (1) в (2), далее в (3), что приводит к единственному уравнению с одним неизвестным.
9*. Ответ: |
θ ≈ 3,4 . |
|
*************** |
Задача201
С какого максимального расстояния Lmax наблюдатель может заметить ночью огонек папиросы, если сила света папиросы
I = 2,5 10−3 кд, |
а |
наименьший |
световой |
поток, |
воспринимаемый глазом, равен Ф =10−13 лм и поверхность зрачка глаза в темноте S = 0,4 см2 ?
- 279 -