Добавил:

Vezen Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

Физика

Файл:

Методика решения задач по оптике для студентов инженерных специальностей

.pdf

Скачиваний:

937

Добавлен:

20.06.2014

Размер:

3.07 Mб

Скачать

☆

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3522 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Задача121

Постоянная дифракционной решетки	d = 2,5 мкм.	Найти
линейную дисперсию DF решетки для	λ = 589 нм в	спектре

m = 1 (первого порядка), если дифракционную картину на экран проецирует линза с оптической силой D = 6 дп.

1*. Дано:

d = 2,5 мкм = 2,5 10-6м,

λ = 589 нм = 5,89 10-7м,

m = 1,

D = 6 дп.

DF – ?

Решение.

2* ───

4*. Составим полную систему уравнений для нахождения искомой величины DF :

	Dψ =				m
(1)						,
(1)			d		cosψ	,
			d		cosψ
	d sinψ = mλ,
(2)	d sinψ = mλ,
	DF = F Dψ ,
(3)	DF = F Dψ ,
	D =	1
(4)		1		.
(4)				.
		F

Система четырех уравнений (1) – (4) замкнута, так как содержит четыре неизвестные величины: Dψ , ψ , DF , D .

9*. Ответ:	DF ≈ 6,9 104 .
	***************

Задача122

Тело шарообразной формы радиуса R = 5 см имеет мощность

излучения N = 15000 Вт.		Длина		волны,	на которой		это	тело
имеет максимальную	излучательную				способность,			равна
λm = 590 нм. Найти	разницу			Т в измерениях		цветовой и
радиационной температур исследуемого тела.
1*. Дано:					Решение.
R = 5 см = 5 10-2м,				2* ───			полную
				4*.	Составим		полную
N = 15000 Вт = 1,5 104 Вт,			систему		уравнений			для
			нахождения		искомой	величины
λ = 590 нм = 5,9 10-7м.			Т:
λ = 590 нм = 5,9 10-7м.
m

- 210 -

Т – ?								(1)

b = 2,9 10−3м К,								(2)

		−8	(м	2		4		(3)
σ =		−8		2		4	.
σ =	5,67	10 Вт			К		.
	5,67	10 Вт			К		)	(4)
								(5)

Tц = b λm , N = kσT 4S, S = 4πR2 , T p= T 4 k ,

T = Tц −T p.

Система пяти уравнений (1) – (5) не замкнута, так как содержит шесть неизвестных величин: Tц, Тр, k, S, Т, Т .

Однако уравнения (2), (4) линейно зависимы относительно переменных k, Т. Поэтому рассматриваемая система однозначно

разрешима относительно искомой величины			T .
9*. Ответ:		T ≈ 3,2 103 К.
	***************
		Задача123
Фотоны с	энергией W = 5 эВ вырывают		фотоэлектроны из
металла	с работой	выхода A = 4,7 эВ. Определите
максимальный импульс		pmax , передаваемый поверхности этого

металла при вылете электрона.

1*. Дано:

W = 5 эВ =

= 5 1,6 10-19 Дж,

A = 4,7 эВ =

= 4,7 1,6 10-19 Дж.

pmax – ?

me = 9,1 10−31кг, c = 3 108м/с.

Решение.

2* ───

4*. Составим полную систему уравнений для нахождения искомой величины pmax :

(1)	W = A +T,
		p	2
					W << mec2.
(2)	T =		max	,

		2me

Система двух уравнений (1) – (2) замкнута, так как содержит две неизвестные величины: T, pmax .

9*. Ответ: pmax ≈ 3,0 10−25кг мс.

***************

- 211 -

Задача124

Нормированная сферически симметричная волновая функция, описывающая 1s-состояние электрона в атоме водорода, имеет

вид ψ(r) =

-r a , где r −

расстояние электрона от ядра,

πа3

а = 0,53 10−10 м−первый

боровский

радиус.

Определить

среднее значение функции

1 .

1*. Дано:

2* ───

Решение.

-r a ,

ψ(r) =

πа3 e

4*.

Составим

полную

систему

уравнений

для

нахождения

искомой

а = 0,53 10−10 м.

величины

– ?

ψ (r)=

e−r a ,

(1)

πa3

∫

ψ (r)

4πr2dr,

(2)

r1 r

(3)

= 0,

r2 = ∞.

(4)

Система четырех

уравнений (1) – (4) замкнута, так как

содержит четыре неизвестные величины: ψ,

1 , r ,

r .

9*. Ответ:

≈ 1,9 1010м−1.

***************

Расстояние d

Задача125

от предмета до вогнутого сферического зеркала

равно

d = 2R ,

где

R − радиус кривизны зеркала.

Определить

оптическую силу зеркала D , если расстояние от изображения до

зеркала равно

= 30 см.

- 212 -

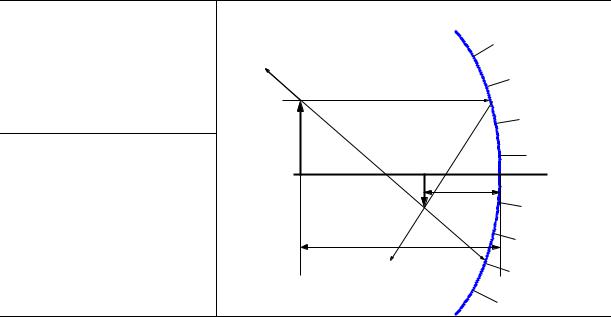
1*. Дано:			Решение.
d = 2R ,			2*.
f = 30 см = 3 10-1	м.	B
f = 30 см = 3 10-1	м.
D – ?			.	A1 F.	.O
		A	.	A1 F.	.O
		A	2F=R		f
				B1	f
			d=2R	B1
			d=2R
4*. Составим полную систему уравнений для нахождения
искомой величины D :

	1		1				1
(1)		+			=			,
(1)	d	+		f	=		F	,
	d			f			F
	R = 2F,
(2)	R = 2F,
	d = 2R,
(3)	d = 2R,
	D =			1
(4)				1		.
(4)						.
				F

Система четырех уравнений (1) – (4) замкнута, так как содержит четыре неизвестные величины: d, R, F, D .

9*. Ответ:

D ≈ 4,4 дп.

***************

Задача126

Монохроматический свет падает нормально на поверхность воздушного клина n0 =1, причем расстояние между некоторыми

интерференционными полосами		S1 = 0,4 мм. Определить
расстояние S2	между этими	же интерференционными

полосами, если пространство между пластинками, образующими клин, заполнить прозрачной жидкостью с показателем преломления n1 =1,3 .

- 213 -

1*. Дано:

2*.

Решение.

n0 =1,

S1 = 0,4 мм =

= 4 10-4м,

n1 =1,3 .

α = α1=α2

hk+m

S2 – ?

k k+1

k+m-1

k+m

4*. Составим

полную систему уравнений для нахождения

искомой величины

S2 :

(1)

2hk n0 ± λ 2 = (2k + 1)λ 2,

(hk +m − hk )= α

(I )

(2)

tgα

≈α

(3)

= (2(k + m)+ 1)λ 2,

n ± λ 2

+m 0

2Hk n1 ± λ 2 = (2k + 1)λ 2,

(4)

(Hk +m − Hk )= α2 ,

(II ) (5)

tgα2 ≈ α2

n ± λ 2 = (2(k + m)+ 1)λ 2,

(6)

k +m 1

(7)

α1 = α2 .

Система семи уравнений (1) – (7) не замкнута, так как

содержит

десять

неизвестных

величин:

hk , hk +1,

m, α1,

α2 , Hk ,

Hk +1, λ, S2 . Однако уравнения (1)

– (3) и (4) – (6) линейно зависимы в каждой из подсистем соответственно относительно переменных hk , hk +1, k и

Hk , Hk +1, k ; подсистемы (I), (II) и уравнение (7) линейно зависимы относительно величин λ, m . Обозначив hk +m − hk =θ и Hk +m − Hk =η , вычитая затем из (3) уравнение (1), а также из

(6) уравнение (4), получим две упрощенные незамкнутые подсистемы уравнений в совокупности с уравнением (7).

- 214 -

Полученная таким образом система без особых осложнений приводит к искомой величине S2.

9*. Ответ: S2 ≈ 3,1 10−4м = 0,31 мм.

***************

Задача127

При нагревании абсолютно черного тела длина волны, на которую приходится максимум излучательной способности, изменилась от λ1 = 690 нм до λ2 = 500 нм. Во сколько раз θ

увеличилась при этом интегральная излучательная способность тела?

1*. Дано:			2* ───	Решение.
λ		= 690 нм = 6,9 10-7 м,	2* ───
1			4*. Составим полную систему
			4*. Составим полную систему
λ	2	= 500 нм = 5 10-7 м.	уравнений для нахождения искомой
	2		величины θ :	λ1T1 = b,
			(1)	λ1T1 = b,

θ – ?				λ2T2 = b,
θ – ?			(2)	λ2T2 = b,
			(3)	E	1	=σT 4			,
					1			1
			(4)	E	2	=σT 4			,
					2			2
			(5)	θ = E			2	E .
							2		1

Система пяти уравнений (1) – (5) замкнута, так как содержит пять неизвестных величин: T1, Ò2 , E1, E2 , θ .

9*. Ответ:	θ ≈ 3,6 .
	***************

Задача128

На плоский алюминиевый электрод падает ультрафиолетовое излучение с длиной волны λ = 90 нм. На какое максимальное расстояние d от его поверхности может удалиться фотоэлектрон, если вне электрода имеется однородное электрическое поле напряженностью E = 8 В/см, задерживающее этот фотоэлектрон? Красная граница фотоэффекта для алюминия λ0 = 330 нм.

- 215 -

1*. Дано:

λ = 90 нм = 9 10-8м,

E = 8 В/см = 8 102 В/м,

λ0 = 330 нм = 3,3 10-7м.

d – ?

h = 6,63 10−34 Дж с, e = 1,6 10−19 Кл,

c = 3 108м/с.

Решение.

2* ───

4*. Составим полную систему уравнений для нахождения искомой величины d :

		hc = A + T ,
	(1)	hc = A + T ,
		λ
		T = eU,
	(2)	T = eU,
		U = Ed,
	(3)	U = Ed,
		hc
		hc
		A = λ0 .
	(4)	A = λ0 .

Система четырех уравнений (1) – (4) замкнута, так как

содержит четыре неизвестные величины: T,

U, d .

9*. Ответ:

d ≈ 1,3 10−2м = 1,3 cм.

***************

Задача129

Вычислить отношение неопределенностей

скоростей

электрона

(его

координата установлена

точностью

до

x = 10−4м) и пылинки массой m = 10−13кг (ее координата

x2 = 10−4м).

установлена с точностью до

Решение.

1*. Дано:

2* ───

= 10−4

м,

4*. Составим полную систему

m = 10−13кг,

уравнений

для

нахождения

искомой

величины η :

x2 = 10

−4

м.

(1)

x m

= h,

η – ?

(2)

x2m υ2 = h,

me = 9,1 10−31кг.

υe

η =

(3)

- 216 -

Система трех уравнений (1) – (3) замкнута, так как
содержит три неизвестные величины:							υe ,			υ2, η.
9*. Ответ:			η ≈ 1,1 1017 .
			***************
			Задача130
Собирающая линза дает действительное изображение с
увеличением в θ = 2 раза. Определить фокусное расстояние F
линзы, если расстояние между линзой и изображением равно
f = 25 см.
1*. Дано:							Решение.
θ = 2,				B
				B
f = 25 см = 2,5 10-1м.						d
f = 25 см = 2,5 10-1м.			.A		F.					.F	A.1
			.A		F.			C		.F	A.1
			2F
										f
F – ?										B1
										B1
4*. Составим полную систему уравнений для нахождения
искомой величины F :				1		1		1
				1	+	1	=	1	,
			(1)	d	+	f	=	F	,
				d		f		F
						f
				θ	=	f	.
			(2)	θ	=	d	.
						d
Система двух уравнений (1) – (2) замкнута, так как содержит
две неизвестные величины: d,				F .
9*. Ответ:		F ≈ 8,3 10−2м = 8,3 см.
			***************
			Задача131
Какова должна быть постоянная d							дифракционной решетки,
чтобы в	спектре первого порядка (m = 1) были разрешены
линии спектра		калия	λ1 = 404,4 нм и					λ2 = 404,7 нм?			Рабочая
длина решетки L = 3 см.
				- 217 -

1*. Дано:					Решение.
m = 1,					2* ───
λ = 404,4 н = 4,044 10-7					4*. Составим полную систему
λ = 404,4 н = 4,044 10-7				м,	уравнений	для				нахождения
1					искомой величины d :
					искомой величины d :
λ2 = 404,7 н = 4,047 10			-7	м,
λ2 = 404,7 н = 4,047 10				м,	(1)	A = mN ,
					(1)	A = mN ,
									λ2
L = 3 см = 3 10	-2	м.				A =			λ2
					(2)						,
					(2)		λ2			− λ1	,
							λ2			− λ1
						d =		L
d – ?					(3)			L		.
d – ?					(3)					.
								N

Система трех уравнений (1) – (3) замкнута, так как содержит три неизвестные величины: A, N , d .

9*. Ответ: d ≈ 2,2 10−5м = 22 мкм.

***************

Задача132

Считая, что атмосфера поглощает k1 = 10% лучистой энергии,

посылаемой Солнцем, найти мощность излучения N , получаемую от Солнца горизонтальным участком Земли площадью S = 0,5 га. Высота Солнца над горизонтом ψ = 30°.

Излучение Солнца считать близким к излучению абсолютно черного тела (степень черноты k2 = 0,95). Температура

поверхности Солнца	T = 5800 К,		расстояние от		Солнца	до
Земли R = 150 Гм, радиус Солнца Rс = 695 Мм.
1*. Дано:		Примечание:		воспользуйтесь
k1 = 10%,		определением		освещенности
		поверхности		из	раздела
S = 0,5 га = 5 103м2 ,		«Фотометрия» и		соответствием
		между	фотометрическими			и
		общими		физическими
		величинами; см. также решение
		задачи № 33 данного пособия.

- 218 -

R = 150 Гм = 1,5 1011м,				Решение.
R = 695 Мм = 6,95 108		м,		*		2R
с				*		oT
T = 5800 К = 5,8 103 К,				2 .		oT
ψ = 30°,			S		R
			S	α
k2 = 0,95.				α
k2 = 0,95.
N – ?				ψ
N – ?
σ = 5,67 10−8 Вт (м2 К4 ).
4*.	Составим полную		систему	уравнений	для	нахождения
искомой величины N :

(1)	N = ESc S				(1 − k	100)cosα
			4πR	2	1
			4πR
(2)	α = π 2 −ψ ,

(3)	E = k σT 4				,
			2
(4)	S	c	= 4πR2 .
		c		c
Система четырех уравнений (1)						– (4) замкнута, так как
содержит четыре неизвестные величины: N , E, α, Sc .
9*. Ответ:	N ≈ 2,9 106 Вт = 2,9 МВт.

***************

Задача133

Определить длину волны λ излучения, способного вырвать с поверхности серебра фотоэлектроны, максимальная скорость которых υmax = 1000 км/с, если работа выхода электронов из

серебра равна A = 4,7 эВ.

- 219 -

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3522 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Соседние файлы в предмете Физика

#
20.06.201412.08 Mб396Вычислительная фотоника.pdf
#
20.06.20142.75 Mб156Исследовательская работа Исследование свойств глаза и создание программы корректировки зрения с помощью специальных упражнений.doc
#
20.06.20143.07 Mб937Методика решения задач по оптике для студентов инженерных специальностей.pdf
#
20.06.2014514.56 Кб89Определение модуля Юнга из растяжения проволоки на приборе Лермантова (лр).docx
#
20.06.2014769.39 Кб381Ответы на тест к экзамену по Физике Оптика.pdf
#
20.06.20143.84 Mб99Отчеты по лабам Оптика 2011-2012 КИ МГОУ.pdf
#
20.06.201479.07 Кб276Проверка основного закона вращения твёрдого тела на крестообразном маятнике.doc
#
20.06.2014346.96 Кб21РГР Зрительная труба Кеплера - КИ МГОУ.pdf