Тематика практических занятий. Тема: «Финансовые риски и управление ими»

(1 час)

Методические рекомендации

Финансовый риск, как и любой риск, имеет математически выраженную вероятность наступления потери, которая опирается на статистические данные и может быть рассчитана с достаточно высокой точностью. Чтобы количественно определить величину финансового риска, необходимо знать все возможные последствия какого-нибудь отдельного действия и вероятность самих последствий. Вероятность означает возможность получения определенного результата. Применительно к экономическим задачам методы теории вероятности сводятся к определению значений вероятности наступления событий и к выбору из возможных событий самого предпочтительного исходя из наибольшей величины математического ожидания. Иначе говоря, математическое ожидание какого-либо события равно абсолютной величине этого события, умноженной на вероятность его наступления.

Вероятность наступления события может быть определена объективным методом или субъективным. Объективный метод определения вероятности основан на вычислении частоты, с которой происходит данное событие. Субъективный метод определения вероятности основан на использовании субъективных критериев, которые основываются на различных предположениях. К таким предположениям могут относиться суждения оценивающего, его личный опыт, оценка эксперта, мнение финансового консультанта и т.п. Когда вероятность определяется субъективно, то разные люди могут устанавливать разное ее значение для одного и того же события и таким образом делать различный выбор.

В финансовом менеджменте для оценки степени финансового риска используются два критерия:

- среднее ожидаемое значение (средневзвешенное значение);

- колеблемость (изменчивость) результата.

Среднее ожидаемое значение измеряет результат, который мы ожидаем получить в среднем. Эта величина представляет собой обобщенную характеристику и не позволяет принять решения в пользу какого-либо варианта вложения капитала. Поэтому для окончательного принятия решения оценивают колеблемость результата. Для этого на практике обычно применяют такие критерии, как: дисперсия и среднее квадратическое отклонение. Эти критерии являются мерами абсолютной колеблемости. Для анализа обычно используется коэффициент вариации, который показывает степень отклонения полученных результатов. Чем больше величина коэффициента, тем сильнее колеблемость: до 10% - слабая колеблемость, 10-25% - умеренная колеблемость, свыше 25% - сильная колеблемость.

Для расчета дисперсии используется формула:

G ² = ,

где: G ² – дисперсия;

х - ожидаемое значение для каждого случая наблюдения;

- среднее ожидаемое значение;

п - число случаев наблюдения (частота).

Среднее квадратическое отклонение определяется по формуле

G = ,

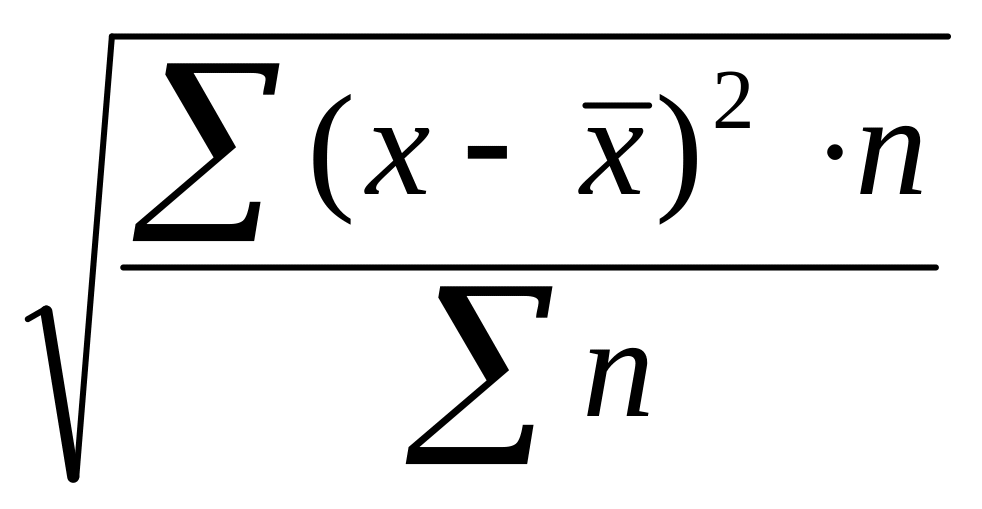где: G – квадратическое отклонение.

При равенстве частот имеем частный случай:

G ² = ;

G = .

Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости.

Количественно риск инвестора характеризуется оценкой вероятной величины максимального и минимального доходов. При этом чем больше диапазон между этими величинами при равной их вероятности, тем выше степень риска.

Когда известны минимальное и максимальное значение результата, а вероятности их наступления приблизительно равны, то для расчета дисперсии применяется следующая формула:

G ² = Р_{max *} (х_max – )² + Р_{min *} ( - х_min )² ;

G = ; V = ,

где: G ²- дисперсия;

Р_max - вероятность получения максимального дохода (прибыли, рентабельности);

Р_min – вероятность получения минимального дохода (прибыли, рентабельности);

х_max – максимальная величина дохода (прибыли, рентабельности);

- средняя ожидаемая величина дохода (прибыли, рентабельности);

х_min - минимальная величина дохода (прибыли, рентабельности);

G - среднее квадратическое отклонение;

V - коэффициент вариации.

В договор страхования могут вноситься различные оговорки и условия, которые носят название «клаузула». Одной из них является франшиза.

Франшиза – это освобождение страховщика от возмещения убытков, не превышающих определенного размера. Размер франшизы означает часть убытка, не подлежащую возмещению со стороны страховщика. Эта часть убытка определяется страховым полисом. Франшиза выступает в абсолютных или относительных величинах к страховой сумме и оценке объекта страхования. Франшиза может быть установлена и в процентах к величине ущерба. При включении в договор страхования франшизы страховщик предоставляет страхователю скидку с тарифной ставки страхового взноса.

Различаются два вида франшизы: условная, безусловная.

Под условной, или интегральной (невычитаемой), франшизой понимается освобождение ответственности страховщика за ущерб, не превышающий установленной суммы, и его полное покрытие, если размер ущерба превышает франшизу. Условная франшиза вносится в форме специальной оговорки (клаузулы) в страховой полис. Такая клаузула делается в форме записи «свободно от Х процентов» (где Х – 1,2,3 – величина процента от страховой суммы). Если ущерб превышает установленную франшизу, то страховщик обязан выплатить страховое возмещение полностью, не обращая внимания на сделанную оговорку.

Безусловная, или эксцедентная (вычитаемая), франшиза означает, что данная франшиза применяется в безоговорочном порядке без всяких условий. При безусловной франшизе ущерб во всех случаях возмещается за вычетом установленной франшизы. Безусловная франшиза оформляется с помощью клаузулы в страховом полисе, которая обычно имеет следующий текст записи: «свободно от первых Х процентов» (где Х процентов вычитаются всегда из суммы страхового возмещения независимо от величины ущерба). При безусловной франшизе страховое возмещение равно величине ущерба за минусом величины безусловной франшизы.

При страховании по действительной стоимости имущества сумма страхового возмещения определяется как фактическая стоимость имущества на день заключения договора. Страховое обеспечение равно величине ущерба. При страховании по системе пропорциональной ответственности величина страхового возмещения определяется по формуле

В = С * У : Ц,

где В – величина страхового возмещения, руб.;

С – страховая сумма по договору, руб.;

У – фактическая сумма ущерба, руб.;

Ц – стоимостная оценка объекта страхования, руб.

При страховании по системе «дробной части» устанавливаются две страховые суммы, одна из которых называется показанной стоимостью. По этой стоимости страхователь обычно получает покрытие риска, выражаемое натуральной дробью или в процентах. Ответственность страховщика ограничена размерами дробной части. Поэтому страховая сумма меньше показанной стоимости и ее дробной части. Страховое возмещение равно ущербу, но не может быть выше страховой суммы.

Если показанная стоимость равна действительной стоимости объекта, то страховое возмещение определяется, как и при страховании, по системе первого риска. Если показанная стоимость меньше действительной стоимости, то для расчета страхового возмещения применяют следующую формулу:

В = П * У / Ц,

где В – величина страхового возмещения, руб.;

П – показанная стоимость, руб.;

У – фактическая сумма ущерба, руб.;

Ц – стоимостная оценка объекта страхования, руб.

При страховании по восстановительной стоимости величина страхового возмещения за объект равна цене нового имущества соответствующего вида. Износ имущества не учитывается. При страховании имущества страховая сумма не должна превышать его действительной стоимости на момент заключения договора (страховой стоимости). Страховое возмещение не может превышать размера прямого ущерба застрахованному имуществу страхователя или третьего лица при страховом случае, если договором страхования не предусмотрена выплата страхового возмещения в определенной сумме.

Вероятность риска деятельности страховщика определяется следующими показателями.

1. Частота страховых событий – это количество страховых случаев на один объект страхования.

2. Коэффициент кумуляции риска, исчисляемый отношением числа пострадавших объектов к числу страховых событий. Он показывает, сколько застрахованных объектов может быть настигнуто страховым случаем.

3. Убыточность страховой суммы – это отношение суммы выплаченного страхового возмещения к страховой сумме всех объектов страхования.

4. Тяжесть ущерба (У) показывает, какая часть страховой суммы уничтожена; она определяется по формуле

У = ,

где В – сумма выплаченного страхового возмещения, руб.;

n – число объектов страхования, ед.;

С – страховая сумма, руб.;

m – число пострадавших объектов в результате страхового случая, ед.

Финансовая устойчивость страховых операций характеризуется дефицитом средств или превышением доходов над расходами страховщика в целом по страховому фонду. Степень вероятности дефицита средств определяется коэффициентом В.С. Коньшина:

К_к = ,

где К_к – коэффициент В.С. Коньшина;

g – средняя тарифная ставка по всему страховому портфелю, руб.;

n – число застрахованных объектов, ед.

Чем меньше величина этого коэффициента, тем финансово-устойчивее страховая операция.

Превышение доходов над расходами выражается в коэффициенте финансовой устойчивости страхового фонда:

К_у = ,

где К_у – коэффициент устойчивости страхового фонда;

Д – сумма доходов страховщика за тарифный период, руб.;

Р – сумма расходов страховщика за тарифный период, руб.;

З – сумма средств в запасных фондах, руб.

Чем больше величины этого коэффициента, тем финансово-устойчивее страховая компания.

Задача 1. Выберете наиболее приемлемый вариант вложения капитала, если известно, что при вложении капитала в мероприятие А прибыль в сумме 450 тыс. руб. была получена в 24 случаях из 40 возможных инвестиций, в мероприятие Б прибыль в сумме 500 тыс. руб. была получена в 20 случаях из 50 возможных инвестиций.

Задача 2. Имеются данные о получении прибыли при вложении капитала в: мероприятие А – прибыль в сумме 400 тыс. руб. получена в 36 случаях; в сумме 500 тыс. руб. – в 48 случаях; в сумме 450 тыс. руб. – в 36 случаях; мероприятие Б – прибыль в сумме 550 тыс. руб. получена в 27 случаях; в сумме 500 тыс. руб. – в 45 случаях; в сумме 350 тыс. руб. – в 18 случаях. Рассчитать среднее ожидаемое значение прибыли при различных вариантах вложения капитала и выбрать из них наиболее приемлемый.

Задача 3. При вложении капитала в мероприятие А сумма получаемой прибыли колеблется от 400 до 500 тыс. руб. Вероятность получения минимального значения прибыли равна 0,3, максимального значения – 0,4.

При вложении капитала в мероприятие А сумма получаемой прибыли колеблется от 350 до 550 тыс. руб. Вероятность получения минимального значения прибыли равна 0,2, максимального значения – 0,3.

Выберете наименее рискованный вариант вложения капитала.

Задача 4. Рассчитать сумму страхового возмещения по системе пропорциональной ответственности.

Стоимостная оценка объекта страхования – 10 млн. руб., страховая сумма – 2,5 млн. руб., ущерб страхователя в результате повреждения объекта – 5 млн. руб.

Задача 5. Рассчитать сумму страхового возмещения по системе первого риска.

Автомобиль застрахован по системе первого риска на сумму 5 млн. руб. Стоимость автомобиля – 7 млн. руб. Ущерб страхователя в связи с повреждением автомобиля – 3,6 млн. руб.

Задача 6. Рассчитать сумму страхового возмещения по системе первого риска.

Автомобиль застрахован по системе первого риска на сумму 6 млн. руб. Стоимость автомобиля - 9 млн. руб. Ущерб страхователя в связи с аварией автомобиля составит 8 млн. руб.

Задача 7. Рассчитать размер страхового платежа и страхового возмещения.

Хозяйствующий субъект застраховал свое имущество сроком на 1 год с ответственностью за кражу со взломом на сумму 1000 млн. руб. Ставка страхового тарифа – 0,3% страховой суммы. По договору страхования предусмотрена безусловная франшиза в размере 50 тыс. руб., при которой предоставляется скидка к тарифу 4%. Фактический ущерб страхователя составил 10 млн. руб.

Задача 8. Рассчитать размер страхового платежа и страхового возмещения.

Хозяйствующий субъект застраховал свое имущество сроком на 1 год с ответственностью за кражу со взломом на сумму 400 млн. руб. Ставка страхового тарифа – 0,3% страховой суммы. По договору страхования предусмотрена условная франшиза «свободно от 1%». Скидка к тарифу – 2%. Фактический ущерб страхователя составил 2 млн. руб.

Задача 9. Рассчитать размер страхового платежа и страхового возмещения.

Хозяйствующий субъект застраховал свое имущество сроком на 1 год с ответственностью за кражу со взломом на сумму 600 млн. руб. Ставка страхового тарифа – 0,3% страховой суммы. По договору страхования предусмотрена условная франшиза «свободно от 1%». Скидка к тарифу – 2%. Фактический ущерб страхователя составил 10 млн. руб.

Задача 10. Рассчитать показатели страхования в двух регионах: частота страховых событий, коэффициент кумуляции риска, убыточность страховой суммы, тяжесть ущерба. Выбрать наименее убыточный регион. Данные для расчета приведены в таблице.

Показатели по страхованию объектов

Показатели	Регион 1	Регион 2
Число застрахованных объектов, ед.	26000	3800
Страховая сумма застрахованных объектов, млн. руб.	100520	29200
Число пострадавших объектов, ед.	9740	2000
Число застрахованных случаев, ед.	8650	1850
Страховое возмещение, млн. руб.	1960	3000

Задача 11. Рассчитать коэффициент В.Ф. Коньшина и выбрать наиболее финансово устойчивую страховую операцию.

По страховой операции №1 количество договоров страхования – 1,2 млн. руб., средняя ставка-нетто с 1 руб. страховой суммы – 0,003 руб. По страховой операции №2 количество договоров страхования – 1,5 млн., средняя ставка-нетто с 1 руб. страховой суммы – 0,0035 руб. Критерием выбора наиболее финансово устойчивой страховой компании является коэффициент В.Ф. Коньшина.

Задача 12. Рассчитать коэффициент финансовой устойчивости страхового фонда и выбрать наиболее финансово устойчивую страховую компанию.

Страховая компания №1 имеет страховых платежей 5000 млн. руб., остаток средств в запасном фонде на конец тарифного периода – 45 млн. руб., выплаты страхового возмещения – 4100 млн. руб., расходы на ведение дела – 480 млн. руб. Страховая компания №2 имеет страховых платежей 4000 млн. руб., остаток средств в запасном фонде на конец тарифного периода – 40 млн. руб., расходы на ведение дела – 500 млн. руб., выплаты страхового возмещения – 2000 млн. руб. Критерием выбора наиболее финансово устойчивой страховой компании является коэффициент финансовой устойчивости страхового фонда.