
Бурлака, Кучеренко, Мазоренко, Тищенко, Основы теории механизмов и машин
.pdf
310Лекция 16
Вкинематической паре А – часть массы 1 звена и часть массы 2 звена:
mA m1lOS1 |
l1 m2 lBS2 |
l2 . |
(8.8) |
В кинематической паре B – часть массы |
2 звена и |
||
часть массы 3 звена: |
|
|
|
mB m2 lAS2 |
l2 m3lCS3 |
l3 , |
(8.9) |
и в кинематической паре C – часть массы 3 |
звена: |
||
mC m3lBS3 |
l3 . |
|
(8.10) |
Таким образом, заданный механизм окажется замененным четырьмя массами, сосредоточенными в кинематических парах О, A, B, C (рис.8.3,б). Центр масс S системы mО, mA, mB, mC находится на том же
месте, что и центр масс системы подвижных звеньев 1, 2, 3 заданного механизма. При движении механизма центр масс S движется с ускорением aS , а это означает, что заданный механизм (рис.8.3,а) статически неуравновешен.
Разместим на звеньях 1 и 3 корректирующие массы (противовесы) mк1 и mк3 (рис.8.3,в) с таким расчетом,
чтобы центры масс систем mА, mк1 и mВ, mк3 оказались бы в неподвижных точках О и C . Для этого
суммы статических моментов масс звеньев 1 и 3 относительно точек О и C соответственно должны быть равны нулю:
mк1lк1 mАl1 |
0 |
|
mк1 mАl1 |
lк1 ; |
(8.11) |
mк3lк3 mBl3 |
0 |
|
mк3 mB l3 |
lк3 . |
(8.12) |
Объединим массы, размещенные на звеньях 1 и 3 (рис.8.3,г):
|
; |
|
mO mA mO mк1 |
mС mС mВ mк3 . |
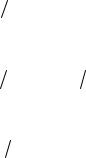
Раздел 8. Уравновешивание механизмов. |
311 |
Таким образом, после размещения противовесов, заданный механизм может быть заменен системой двух неподвижных масс mО и mС . Поэтому, центр масс S этой
системы, а следовательно, и центр масс заданного механизма, но дополненного корректирующими массами mк1 и mк3 будет лежать на неподвижной линии ОС , т.е.
тоже станет неподвижным (рис.8.3,г). А это означает, что статическое уравновешивание заданного механизма достигнуто. Массы mк1 и mк3 противовесов определяются из уравнений (8.11) и (8.12) по предварительно заданным размерам lк1 и lк3.
Статическое уравновешивание кривошипноползунного механизма
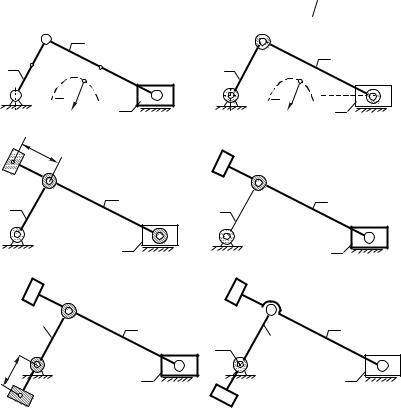
Требуется статически уравновесить кривошипноползунный механизм ОAB (рис.8.4,а), для которого заданы длины подвижных звеньев l1, l2, массы m1, m2 , m3 и
положения центров масс S1, S2 , S3.
Используя уравнения (8.5) и (8.6) заменим массы 1 и 2 звеньев двумя сосредоточенными массами расположив их в соответствующих кинематических парах (рис.8.4,б).
В кинематической паре О будет сосредоточена
часть массы 1 |
звена: |
|
|
|
|
mO m1lAS1 |
l1 . |
|
(8.13) |
В кинематической паре |
А – часть массы |
1 |
звена и |
|
часть массы 2 |
звена: |
|
|
|
|
mA m1lOS1 |
l1 m2 lBS2 l2 . |
|
(8.14) |
В кинематической паре |
B – часть массы |
2 |
звена и |
|
масса 3 звена: |
|
|
|
|
|
mB m2 lAS2 |
l2 m3. |
|
(8.15) |
312 |
Лекция 16 |
Разместим на 2 звене корректирующую массу mк2 (рис.8.4,в) с таким расчетом, чтобы центр масс системыmB, mк2 оказался бы в точке А. Для этого сумма статических моментов масс mB и mк2 относительно точки А должна быть равна нулю:
|
|
mк2lк2 mВl2 0 |
|
mк2 mВ l2 |
lк2 . (8.16) |
||||
|
А |
2 |
|
|
|
А |
mA |
2 |
|
1 |
S |
S |
2 |
В,S3 |
1 |
|
|
||
|
|
S |
|
m |
|||||
|
1 S |
|
|
|
|
||||
О |
|
|
|
|
О |
m |
|
|
B |
|
|
|
|
|
|
В |
|||
|
aS |
3 |
|
|
О |
aS |
3 |
||
|
|
а) |
|
|
|
|
б) |
|
|
|
lк2 |
|
|
|
|
|
|
|
|
mк2 |
|
А |
2 |
|
|
|
А |
|
|
1 |
|
mA |
|
1 |
mA |
2 |
|
||
|
|
mB |
В |
||||||
О |
m |
|
|
О |
m |
|
|
||
|
|
В |
|
|
|
||||
|
О |
|
|
|
|
|
|
||
|
|
|
3 |
|
О |
|
3 |
|
|
|
|
в) |
|
|
|
г) |
|
||
|
|
|
|
|
|
|
|
||
|
1 |
А |
2 |
|
|
|
А |
2 |
|
|
m |
|
|
|
1 |
|
|||
|
|
A |
|
В |
S |
|
|
В |
|
lк1 |
О |
mО |
|
|
|
|
|||
|
|
3 |
О |
mО |
|
3 |
|||
|
|
|
|
|
|
|
|
||
mк1 |
д) |
|
|
|
|
е) |
|
|
|
|
|
|
|
Рис. 8.4. |
|
|
|
|
|
|
Объединим массы, размещенные на 2 звене |
|
|||||||
(рис.8.4,г): |
mА mА mВ mк2 . |
|
(8.17) |
||||||
|
|
|
|
||||||
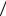
Раздел 8. Уравновешивание механизмов. |
313 |
Разместим на 1 звене корректирующую массу mк1 (рис.8.4,д) с таким расчетом, чтобы центр масс системыmА, mк1 оказался бы в точке О. Для этого сумма статических моментов масс mA и mк1 относительно точки О должна быть равна нулю:
mк1lк1 mАl1 0 |
|
mк1 mАl1 |
lк1 . |
|
(8.18) |
|
Объединим массы, |
размещенные |
на |
звене 1 |
|||
(рис.8.4,е): |
|
|
|
|
|
|
|
|
|
|
|
(8.19) |
|
mO m1 m2 m3 mк1 mк2 . |
|
|||||
Таким образом, после размещения противовесов |
||||||
заданный механизм может быть заменен одной |
|
|
|
|||
|
|
|
|
|
S |
|
неподвижной массой mО (рис.8.3,е), т.е. центр масс |
|
|||||
заданного механизма, но дополненного корректирующими массами mк1 и mк2 будет неподвижным. А это означает, что заданный механизм статически уравновешенный.
Если предварительно задать размеры lк1 и lк2 , то массы mк1 и mк2 противовесов определяются из уравнений (8.16) и (8.18).
Таким образом, статическое уравновешивание с помощью метода заменяющих масс состоит в следующем:
каждое звено механизма, за исключением ползунов, надо заменить двумя сосредоточенными массами, расположив их в кинематических парах;
вводя корректирующие массы (противовесы) и объединяя их с заменяющими массами, добиться того, чтобы объединенные массы оказались бы в конечном счете размещенными в неподвижных точках механизма.
314 |
Лекция 16 |
Неполное статическое уравновешивание механизмов
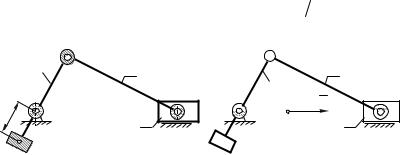
Статическое уравновешивание кривошипноползунного механизма с помощью двух противовесов (рис. 8.4,е) приводит к тому, что установка корректирующей массы mк2 на шатуне 2 сильно удлиняет его, а вместе с тем увеличивает и габариты всего механизма. Такое конструктивное решение довольно редко используется в инженерной практике. Обычно кривошипно-ползунный механизм статически уравновешивается только одним противовесом, размещенным на кривошипе 1.
Уравновесим таким способом кривошипноползунный механизм показанный на рис. 8.4,а.
Используя формулы (8.13) – (8.15) разнесем массы звеньев по кинематическим парам (рис. 8.4,б).
Разместим на 1 звене корректирующую массу mк1 (рис.8.5,а) с таким расчетом, чтобы центр масс системыmА, mк1 оказался бы в точке О. Для этого сумма статических моментов масс mA и mк1 относительно точки О должна быть равна нулю:
|
mк1lк1 mАl1 0 |
|
mк1 mАl1 |
lк1 . (8.20) |
|||||
1 |
А |
2 |
|
|
|
А |
2 |
|
|
mA |
mB |
|
|
1 |
|
mB |
|||
О |
|
|
|
|
S |
aS |
|
||
lк1 mО |
|
|
В |
О |
|
|
|
В |
|
|
3 |
mО |
|
|
3 |
||||
|
|
|
|
|
|
|
|
||
mк1 |
|
а) |
|
|
|
б) |
|
|
|
|
|
|
Рис. 8.5. |
|
|
|
|
|
|

Раздел 8. Уравновешивание механизмов. |
315 |
Объединим массы, размещенные на звене 1 (рис.8.5,б):
mO mО mА mк1 m1 mк1 m2 lBS2 . (8.21) l2
Таким образом, после размещения противовеса mк1 заданный механизм может быть заменен системой двух масс (рис.8.5,б): неподвижной массой mО и горизонтально движущейся массой mB . Центр масс S этой системы, а следовательно, и заданного механизма, но дополненного противовесом mк1 будет двигаться по линии ВО.
Поскольку ускорение aS центра масс подвижных
звеньев, а следовательно, и главный вектор сил инерции направлены вдоль этой линии, то механизм на основание будет оказывать только горизонтальное динамическое воздействие.
Статическое уравновешивание, при котором не ставится задача достижения равенства нулю главного вектора сил инерции, а фиксируется только его линия действия, т.е. задается направление динамического воздействия, называется неполным статическим уравновешиванием.
Неполное статическое уравновешивание очень часто используется на практике, например, в двигателях внутреннего сгорания, насосах, сельскохозяйственных машинах, кузнечнопрессовых станках и т.д.
Схемное уравновешивание механизмов
Полной статической уравновешенности можно достичь и без размещения противовесов, если спроектировать так называемый самоуравновешенный механизм. Примером такого механизма является
316 |
Лекция 16 |
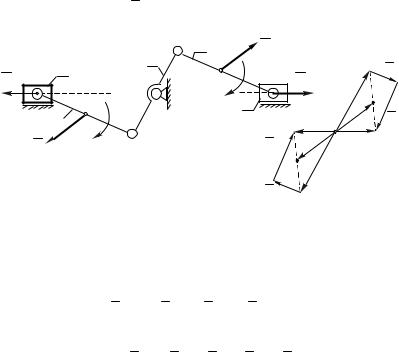
сдвоенный кривошипно-ползунный механизм (рис.8.6,а), используемый для двигателей внутреннего сгорания.
Механизм выполнен кососимметричным, правая и левая шатунно-поршневые группы 2-3 и 4-5 абсолютно одинаковые, центр масс S1 коленчатого вала 1 находится
на оси вращения Fи1 0 .
|
|
|
|
|
А |
2 |
Fи2 |
|
|
F |
D |
5 |
|
|
1 |
S2 |
B |
c |
nDC |
|
|
|
|
|
F |
|
|||
и5 |
|
|
S |
|
О,S1 |
Mи2 3 |
и3 |
s4 |
|
|
|
4 |
4 |
|
|||||
|
|
|
|
|
|
b |
DC |
||
|
|
|
|
|
C |
|
|
||
|
F |
|
M |
|
BA |
|
d |
||
|
и4 |
|
|
и4 |
|
s2 |
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
а) |
|
nBA |
б) |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
Рис. 8.6. |
|
|
|
|
|
План |
|
ускорений |
такого |
механизма так же |
будет |
||
кососимметричным (рис.8.6,б), т.е. ускорения характерных точек попарно равны по величине но противоположны по направлению: аS2 аS4; aB aD. Поэтому главный
вектор сил инерции подвижных звеньев равен:
Fи Fи2 Fи3 Fи4 Fи5 0,
что свидетельствует о полной статической уравновешенности механизма.
Однако, главный момент сил инерции не равен
нулю:
Mи Mи4 Mи2 MО Fи2 MО Fи4 0,
что свидетельствует о моментной неуравновешенности механизма.

Раздел 8. Уравновешивание механизмов. |
317 |
На рис. 8.7, показана схема однорядного двухцилиндрового двигателя внутреннего сгорания. Поскольку ускорения точек B и D (рис. 8.7,б) по величине не равны aB aD , в этом случае достигается только частичное уравновешивание сил инерции.
|
B |
Fи3 |
c s4 |
|
d |
|
|
DC |
|||
Fи2 |
|
|
nDC |
|
|
Mи2 |
S2 |
D |
|
|
|
А |
F |
Mи4 |
|
|
|
|
|
|
|||
|
и5 |
|
|
|
|
|
О,S1 |
S4 |
|
b |
|
|
Fи4 |
|
a |
||
|
|
|
|
||
|
|
C |
|
|
BA s2 nBA |
а) б)
Рис. 8.7.
Однако, в многоцилиндровых двигателях (с числом цилиндров более 6) при определенных углах развала рабочих шеек коленчатого вала можно получить схему механизма, которая будет статически уравновешенной.
В заключение отметим, что статически уравновешенный механизм сохраняет свою статическую уравновешенность при любой угловой скорости начального звена, как постоянной, так и переменной.
8.5. Моментное уравновешивание механизмов
Выше было показано, что моментное уравновешивание можно выполнить только на статически
уравновешенном механизме Фи 0 . Для этого необходимо уравновесить главный момент сил инерции Mи , т.е. добиться условия: Mи 0.
318 |
Лекция 16 |
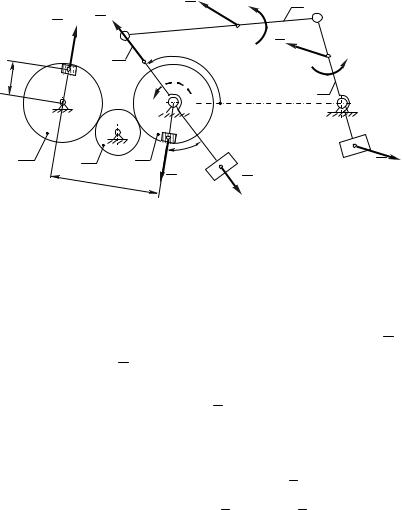
Рассмотрим моментное уравновешивание на примере статически уравновешенного шарнирного четырехзвенного механизма (рис. 8.8). Рассмотрение выполним при условии 1 const.
|
|
|
Fи2 |
Mи2 |
2 |
|
|
Fик Fи1 |
А |
S2 |
|
В |
|
|
|
|
Fи3 |
S3 |
||
|
1 |
|
|
|
||
r |
m |
S1 |
1 |
|
|
Mи3 |
|
|
|
||||
к |
к |
|
|
|
|
3 |
|
Е |
|
|
|
|
|
|
Mи |
О |
|
|
С |
|
|
|
|
|
|||
z3 |
|
|
mк |
mк1 |
|
|
z2 |
z1 |
|
|
mк3 F |
||
|
hк |
|
Fик |
Fик1 |
|
ик3 |
|
|
|
|
|||
|
|
|
|
|
Рис. 8.8.
Главный момент сил инерции механизма определим по зависимости (8.2). При этом необходимо иметь в виду, что предварительно механизм был статически уравновешен, т.е. появились противовесы mк1 и mк3.
Учитывая, что звено OA вращается с постоянной угловой скоростью, то линия действия сил инерции Fи1
первого звена и Fик1 противовеса массой mк1 проходит через точку O и их моменты относительно этой точки
равны нулю. Сила же инерции Fик3 противовеса mк3 |
будет |
создавать момент относительно точки O. |
|
С учетом сказанного, уравнение (8.2) примет вид: |
|
Mи Mи2 Mи3 MO Fи2 |
|
MO Fи3 MO Fик3 . |
(8.22) |

|
|
Раздел 8. Уравновешивание механизмов. |
319 |
||
|
|
Поскольку момент |
Mи |
определяется при условии |
|
|
|
и 0, то его величина |
|
|
|
Ф |
не |
зависит от выбора центра |
|||
приведения. |
|
|
|
||
|
|
Дополним схему механизма (рис. 8.8) рядным |
|||
зубчатым механизмом z1 - z2 |
- z3 . Зубчатое колесо |
z1 |
|||
жестко свяжем со звеном 1, т.е. его угловая скорость равна
1. Равное колесу z1 |
колесо |
z3 |
будет вращаться в ту же |
||||
сторону и с такой же угловой скоростью. |
|
|
|||||
Установим |
два |
одинаковых |
противовеса |
||||
(корректирующие массы) массой |
mк |
каждый, |
которые |
||||
прикрепим |
к зубчатым колесам |
z1 |
и z3 . |
Радиусы rк , |
|||
закрепления |
противовесов |
одинаковы, |
а |
угловые |
|||
координаты противовесов в любом положении механизма отличаются друг от друга на 180 .
Вследствие этого центробежные силы инерции
|
|
|
|
|
|
|
|
|
противовесов массой |
m составят пару сил |
F |
, F |
с |
||||
|
к |
ик |
|
ик |
|
|||
плечом hк (рис. 8.8): |
hк lOЕ sin 1 . |
|
|
|
|
|
|
|
Учитывая, что модуль центробежной силы инерции массы mк равен:
Fк Fк mкrк 12,
то момент пары сил Fик, Fик , который в дальнейшем будем называть корректирующим, составит:
M |
к |
m r 2l |
sin . |
(8.23) |
|
к к 1 OЕ |
1 |
|
Максимального значения корректирующий момент достигает, когда sin 1 1:
M |
к max |
m r 2l |
. |
(8.25) |
|
к к 1 OЕ |
|
|
