1.6.2.Термодинамическая вариантность многокомпонентных многофазных систем.

1.6.3.Правило фаз Гиббса.

В пункте 1.6.1 установлено, что если к-компонентная гетерогенная система состоит из ф равновесно сосуществующих фаз, то должны выполняться равенства (1.6.4)

(1)

. . . . . . . . . . . . . . . . .

С помощью этих условий можно получить правило фаз Гиббса, которое позволяет установить:

• термодинамическую вариантность системы f - число независимых интенсивных параметров состояния, изменение которых в некоторых пределах не нарушает количества равновесно сосуществующих фаз. Согласно данному определению вариантность системы не может быть отрицательной: f ≥ 0;

• максимальное количество фаз, способных находятся в равновесии в k-компонентной системе в условиях постоянства температуры и давления (P = const, T = const).

Вариантность системы определяется разностью между полным числом интенсивных переменных, определяющих состояние ф диффузно не взаимодействующих фаз, и числом уравнений, связывающих эти переменные между собой при фазовом равновесии, а также числом дополнительных условий, налагаемых на интенсивные переменные. Запишем для удобства выражение для вариантности системы в виде «словесной формулы»

f = {полное число интенсивных переменных , определяющих состояние гетерогенной системы c диффузионно изолированными фазами} -

- [число уравнений, связывающих эти переменные в условиях фазового равновесия] -

- (число дополнительно налагаемых условий, ограничивающих вариантность системы)

Предположим, что в каждой из ф фаз присутствуют все k компонент. Тогда выражение в фигурных скобках «словесной формулы» можно представить в виде

{ }= 2+ ф(k-1) (2)

Здесь слагаемое 2 – это два параметра Т и Р, единые для всей системы; (k-1) – число независимо интенсивных параметров состава в каждой фазе, например, мольных долей { }, подчинённых условию . Выражение в квадратных скобках «словесной формулы» равно числу независимых условий (1) на химические потенциалы компонентов в состоянии фазового равновесия, и его можно представить в виде

[ ] = k(ф-1) (3)

Число дополнительно налагаемых условий, ограничивающих вариантность системы, заключённое в круглые скобки «словесной формулы», обозначим через

( ) = (4)

Согласно «словесной формуле» с учетом (2) - (4) имеем

f = 2 + ф(k-1) - k(ф-1) - , (5)

или окончательно

f = 2 + k – ф - (1.6.9)

Формула (1.6.9) представляет собой правило фаз Гиббса. Если , то вариантность системы определяется формулой

f = 2 + k – ф (1.6.10)

В зависимости от числа термодинамических степеней свободы принято различать системы:

• нонвариантные f = 0, состоящие из ф = ф_max = k + 2 фаз, поскольку вариантность подчиняется условию f ;

• моновариантные f = 1, состоящие из ф = k + 1 фаз;

• дивариантные f = 2, состоящие из ф = k фаз.

Например, для однокомпонентной системы максимальное число равновесно сосуществующих фаз ф_max = 3. Состояние, в котором равновесно сосуществуют жидкая, твердая и паровая фазы называют основной тройной точкой. Температуры и давления во всех тройных точках являются индивидуальными характеристиками каждого вещества.

Дополнительными условиями, ограничивающими вариантность системы, могут быть:

1).Закрепление одного из параметров системы Р или Т условиями протекания процесса. Например, изобарное протекание процесса, или изотермное протекание процесса. Это уменьшает реализуемую вариантность системы на единицу.

2)Особенности происходящих в системе физико-химических процессов, накладывающие дополнительные ограничения на число независимых интенсивных параметров состояния системы.

Например, для большинства конденсированных систем изменение внешнего давления в широких пределах пренебрежимо мало влияет на протекающие в ней процессы и превращения. В этих случаях давление можно считать фактически зафиксированным и правило Гиббса можно записывать в виде

f (1.6.11)

Билет 2

Билет 2.1 Структура молекул фуллеренов С₆₀. Фуллерит. Интеркалированные соединения фуллерита. Сверхпроводимость фуллерита и его соединений.

Фуллерен

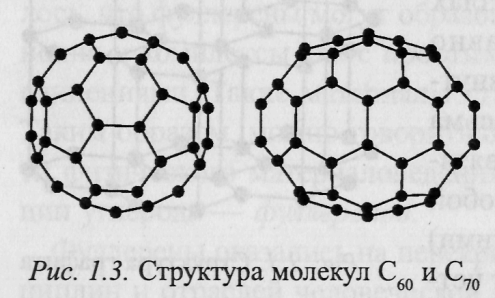
Новая форма углерода является новой по существу [6]. В противоположность первым двум, графиту и алмазу, структура которых представляет собой периодическую решетку атомов, третья форма кристаллического углерода является молекулярной. Это означает, что минимальный элемент ее структуры не атом, а молекула. Оказывается, молекулы чистого углерода могут иметь замкнутую поверхность в форме сферы или сфероида (рис. 1.3).

К ак уже упоминалось выше, атом углерода имеет внешнюю электронную оболочку S²P². Такая оболочка обеспечивает довольно устойчивые связи, когда соседние атомы образуют пяти- и шестиугольники, из которых формируются кластеры углерода. Эта же структура является оптимальной для наиболее устойчивых кластеров углерода. Каркас молекулы С₆₀ состоит из 12 правильных пятиугольников (пентагонов) и 20 неравносторонних шестиугольников (гексагонов). В структуре С₆₀ следует различать два типа связей. Одна из них двойная и является общей стороной двух шестиугольников, а другая — одинарная — является общей стороной пяти- и шестиугольника. Радиус фуллерена – 0,3512 нм. Экспериментальные данные показали, что длина сторон, соединяющих два гексагена, равна 0,139 нм, тогда как длина сторон, соединяющих гексагон с пентагоном, около 0,144 нм [7]. Следовательно, шестиугольники, составляющие структуру молекулы С₆₀, несколько отличаются от правильных, как это имеет место в графите, где стороны шестиугольников равны 0,142 нм. Длинные стороны в сетке связей С₆₀ соответствуют одинарным, а более короткие — двойным связям. Координационное число атома углерода в фуллерене равняется трем. Каждый атом углерода, располагаясь на сферической поверхности молекулы С₆₀, имеет две одинарные и одну двойную связь, что является свидетельством того, что имеет место гибридизация электронных атомных орбиталей типа S-P², как и у графита, из которого фуллерен и образуется.

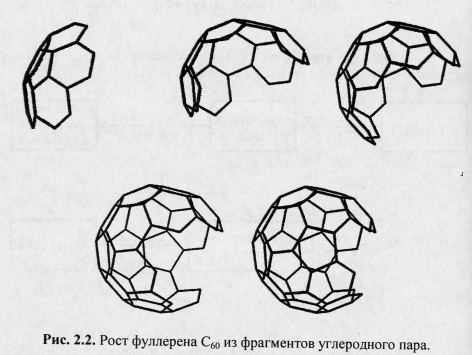
Связь между структурой графита и структурой замкнутой поверхности фуллеренов, видимо, должна проявляться в механизме образования фуллеренов. Модельные представления таковы: при умеренном нагреве графита разрываются связи между отдельными гексагональными сетками графита, и испаряемый слой гексагональной сетки разбивается на отдельные фрагменты. Эти фрагменты представляют собой комбинации шестиугольников, а уже из них идет построение молекулы С_п. Для построения молекулы С₆₀ можно было бы взять десять шестиугольников, содержащих 60 атомов, и объединить их в замкнутую структуру. Однако это невозможно сделать, не разрезая шестиугольники. Дело в том, что правильными шестиугольниками можно легко выложить плоскую поверхность, но нельзя выложить замкнутую поверхность, радиус которой соизмерим со стороной шестиугольника. Однако можно собирать молекулу С₆₀ из фрагментов, которые содержат два и более шестиугольников.

Н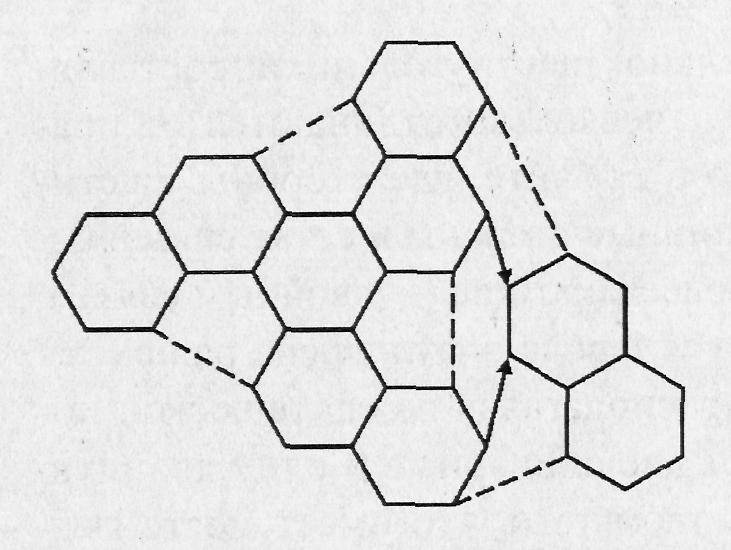 а рис. 1.4 показана схема формирования замкнутого кластера углерода из фрагментов графита. Большой фрагмент, состоящий из семи шестиугольников (30 атомов), сворачивается в объемную структуру. Пунктирные линии замыкают соответствующие стороны пятиугольника. Далее фрагмент, состоящий из двух шестиугольников (10 атомов), образует с большим фрагментом шестиугольник (замыкается стрелками) и два пятиугольника (замыкаются пунктиром). Из полученного таким образом фрагмен-та создается часть кластера С₆₀, содержащая 40 атомов, шесть замкнутых пятиугольников и десять замкнутых шестиугольников. Фуллерен С₆₀ можно получить путем добавления к этому фрагменту еще двух, которые представляют собой двойные шестиугольники [8]. Молекула С_б0 обладает высокой симметрией, близкой к сферической, что позволяет представлять ее как сферическую оболочку, толщина которой составляет около 0,1 нм, а радиус — около 0,36 нм. Схема, которая представлена на рис. 1.4, является чисто умозрительной. Для того, чтобы ее подтвердить, нужны экспериментальные доказательства. Пока же можно отметить, что при испарении графита преобладают малоатомные комплексы, преимущественно С , которые, видимо, последовательно присоединяются к растущему кластеру.

ФУЛЛЕРИТ

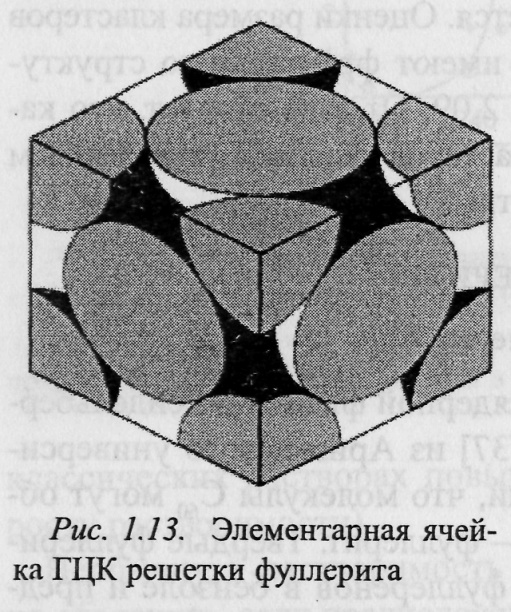
В результате выпаривания растворителя молекулы С₆₀ могут образовывать твердые кристаллы. Эти кристаллы подобны обычным с той лишь разницей что вместо атомов в узлах решетки расположены фуллерены. Такая структура получила название фуллерит. При 300 К структура фуллерита соответствует ГЦК решетке с постоянной а = 1,417 нм.

Элементарная ячейка содержит 8 тетраэдрических и 4 октаэдрические пустоты, каждая из которых окружена соответственно 4 и 6 молекулами С₆₀. Расстояние между ближайшими соседними молекулами равно 1,002 нм. Координационное число молекул фуллерена в ГЦК фазе равно 12. С учетом того, что радиус молекулы С₆₀ равен 0,353 нм, расстояние между ближайшими соседними атомами углерода равно 0,294 нм, что значительно меньше, чем расстояние между гексагональными сетками в графите (0,335 нм). Установлено, что межмолекулярные силы являются ван-дер-ваальсовскими, что согласуется с измерениями изотермической сжимаемости.

Находясь в узлах кристаллической решетки, молекулы С₆₀ испытывают быстрое вращение вокруг своего центра тяжести. По данным ЯМР, частота вращения при Т = 300 К составляет около 10¹² с-¹. Отработанная версия такого поведения молекул С₆₀ в кристалле заключается в том, что молекулы в ГЦК решетке находятся в четырех неэквивалентных положениях (рис. 1.14). Каждая из четырех молекул ГЦК куба вращается на один и тот же угол Г = 24° около одной из четырех осей кристалла в направлении <111>. Локализация вращения осуществляется за счет более богатой электронами С=С связи, которая примыкает к центру пятиугольника соседней молекулы, имеющей более низкую электронную плотность. Все это указывает на то, что между молекулами существует слабое кулоновское взаимодействие.

Используя стандартную алмазную наковальню и рентгеновскую дифракцию от порошка при давлении 1,2 ГПа, авторы [38] нашли, что сжимаемость вдоль оси а, — d(ln a)/dP = 2,3 • 10~¹² см³/дин, оказалась той же самой, что и межслойная сжимаемость вдоль оси с в графите. Изотермическая объемная сжимаемость (-l/V)(dV/dP) = 6,9, 2,7 и 0,18 • 10^-12см²/дин для фуллерита, графита и алмаза соответственно. Фуллерит является самой "мягкой" из твердотельных фаз углерода, имеющей к тому же плотность 1,697 г/см³. Для сравнения плотность графита 2,3 г/см³, а плотность алмаза 3,5 г/см³

	(-l/V)(dV/dP) 10-12см2/дин	Плотность, г/см3
Фуллерит	6,9	1,697
Графит	2,7	2,3
алмаз	0,18	3,5

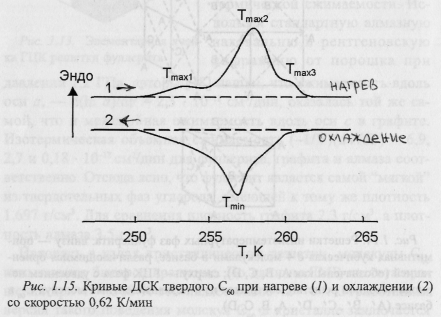
При охлаждении твердого фуллерита в области температур 250 — 260 К обнаружен фазовый переход первого рода, когда ГЦК решетка перестраивается в простую примитивную кубическую решетку. При фазовом превращении постоянная решетки фуллерита почти не изменяется.

Фуллерит С₇₀

Твердый С₇₀ получается, так же как и С₆₀, из раствора толуола. Структура порошка С₇₀ определялась рентгеновской и электронной дифракцией. Фуллерит из С₇₀ кристаллизуется в ГПУ решетку с параметрами а = 1,063 нм и с = 1,739 нм. Растворенные в толуоле молекулы С₇₀ труднее извлекаются из раствора по сравнению с С₆₀. Порошок твердого С₇₀ сублимирует при температуре 810 К в динамическом вакууме. Если сублимированный порошок затем отжигать при 575 К в течение 12 часов, то в результате этой процедуры образуется ГЦК структура с а = = 1,496 нм, в которой содержится 11 % об. ГПУ фазы. В сублимированных кристаллах обнаружены дефекты упаковки, подобные наблюдавшимся в фуллерите С₆₀. Во всех исследуемых образцах фуллерита С₇₀ наблюдается переход в низкотемпературную фазу или смесь фаз, структура которых не установлена. Измерения с помощью ДТА показали два воспроизводимых перехода: один при 276 К, другой при 337 К с теплотой перехода, равной 3,5 ± 0,5 и 2,7 ± 0,3 Дж/г соответственно. Сумма этих величин (6,2 Дж/г) близка теплоте ориентационного перехода, наблюдаемого в твердом С_б0. Рассматривая совершенство отношения с/а в гексагональной фазе и упорядочение в ГЦК фазе, можно прийти к заключению, что молекула С₇₀ является почти сферическим объектом с плотной упаковкой при высоких температурах.

Интеркалированные соединения фуллеритов

Существенные достижения в молекулярной и твердотельной химии привели к синтезу различных соединений С₆₀ с другими элементами. Как только было обнаружено, что молекулы С_т при образовании твердого тела связаны между собой ван-дер-вааль-совскими силами, сразу же возникла мысль использовать это свойство для образования соединений, в том числе таких, которые называются интеркалированными соединениями (соединения с внедренными атомами в кристаллической решетке фуллерита). В интеркалированных соединениях большие тетраэдри-ческие и октаэдрические пустоты в кристалле с ГЦК решеткой образуют слоистые галереи. В то время как основная структура остается неизменной (рис. 1.19 а), металлические свойства достигаются тогда, когда заполняется половина зоны за счет добавления трех электронов на молекулу и образуется вторая псевдоэлектронная система. Металлические свойства возникают при внедрении одновалентных ионов во все три полости твердого С₆₀. Соединения такого типа называют фуллеридами.

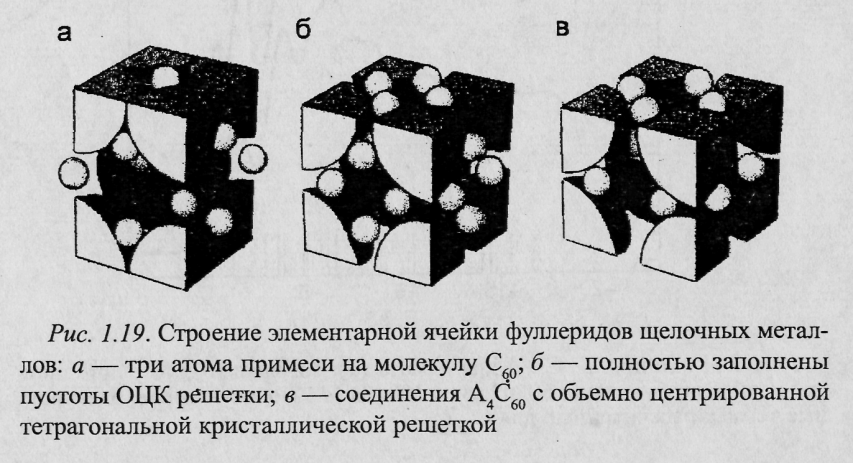
Получение таких соединений сразу же привело к открытию первых сверхпроводников на основе фуллеренов типа М_хС₆₀(М = К, Rb).

Первоначальные результаты по легированию фуллерита щелочными металлами предполагали, что легирование достигает предельного значения при х = 3. Измерения электрического сопротивления в процессе напыления металла на фуллерит показали, что по мере увеличения концентрации металла до х = 3 сопротивление уменьшается до минимальных значений, а затем по мере увеличения х сопротивление растет. Элементный анализ легированного до насыщения К и Cs фуллерита показал, что в пределе образуется композиция М₆С₆₀. Однако внедрение атомов при концентрациях х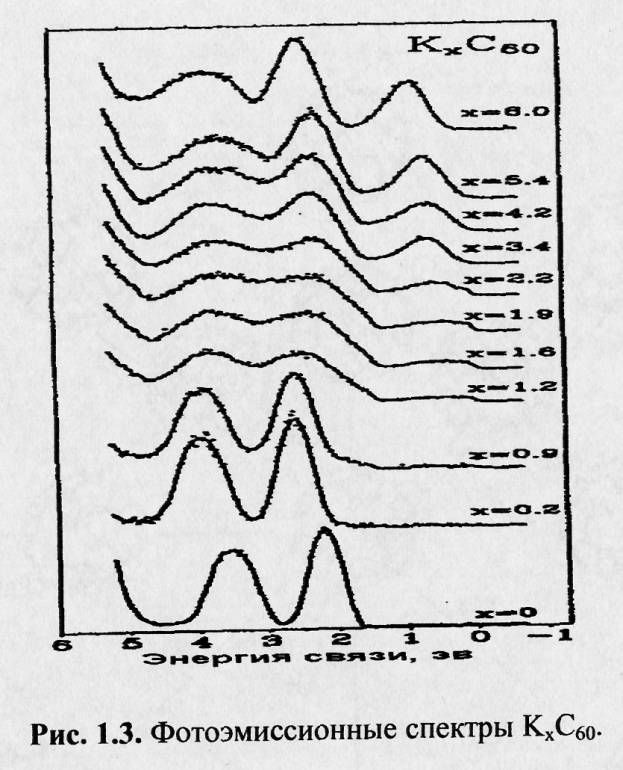 > 3 требует, чтобы сверхрешетка фуллерита преобразовалась в симметрию, отличную от ГЦК, поскольку необходимо иметь более чем три места внедрения на одну молекулу.

П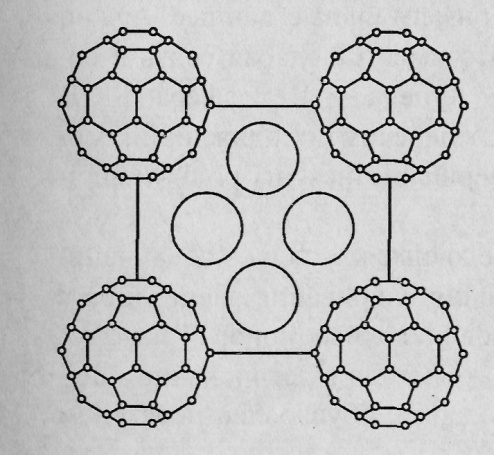 ервые прямые структурные доказательства были получены при использовании легированных до насыщения соединений М₆С₆₀ (М = К, Rb, Cs) [45]. Оказалось, что легирование фуллерита К, Rb, Cs до насыщения сопровождается перестройкой ГЦК решетки в ОЦК с неплотной упаковкой. На рис. 1.20 показана одна из граней такого куба. Согласно схеме, 12 атомов М на ячейку представлены в виде четырех атомов, расположенных, как в решетке алмаза, в эквивалентных положениях. Каждая молекула С₆₀ находится в окружении 24 атомов М, и каждый из этих атомов обусловливает тетрагональность четырех молекул С . Самые короткие расстояния между центрами молекул С₆₀ равны 0,979 и 1,021 нм при легировании калием и цезием соответственно. Отметим, что в нелегированной ГЦК фазе фуллери-та расстояние между ближайшими соседними молекулами С₆₀ равно 1,002 нм. Расстояния между ближайшими соседними атомами С - Cs находятся в интервале 0,338 — 0,370 нм, что сравнимо с величиной, равной 0,320 нм, как суммы ван-дер-вааль-совского радиуса атома углерода и ионного радиуса цезия. Расстояния между атомами Cs — Cs равны 0,415 нм, что значительно больше, чем ионный диаметр, равный 0,334 нм. Таким образом, при легировании фуллерита щелочными металлами получены стехиометрическая ГЦК фаза фуллерида типа М_хС₆₀ (х = = 3), стехиометрические объемно центрированные тетрагональные фазы при х = 4 и х = 6. Первая из них оказалась сверхпроводником. Исследования электрических и других свойств последних двух фаз продолжаются.

Широко известно, что свойства полупроводников можно существенным образом изменять путем их допирования. Допант может либо отдавать свои электроны в зону проводимости полупроводника (допант я-типа), либо забирать электроны из валентной зоны полупроводника (допант р-типа). При обработке фуллерита С₆₀ парами щелочных металлов происходит его допирование по n-типу, электрон щелочного металла попадает в зону проводимости, образованную t_1u-состояниями.

На рис. 1.3 представлены фотоэмиссионные спектры образцов фуллерита С₆₀, допированного калием, т. е К_хС₆о (рисунок взят из [19]). Видно, что при допировании вблизи уровня Ферми (Е_ь = 0) появляется новая полоса, интенсивность которой растет с увеличением концентрации допанта х. Емкость валентной зоны, образованной t_1u -состояниями, ограничена 6-ю электронами (в расчете на одну молекулу фуллерена). Поэтому при 0 < х < 3 проводимость образца растет с увеличением х, а при х = 6 зона проводимости оказывается заполненной полностью и свойства образца зависят от того, какая структура следующей свободной зоны, которая образуется t_lg МО состояниями.

При х = 3 зона проводимости заполнена наполовину. Именно в этом случае, как уже сообщалось, образец приобретает способность переходить в сверхпроводящее состояние при 19 К.

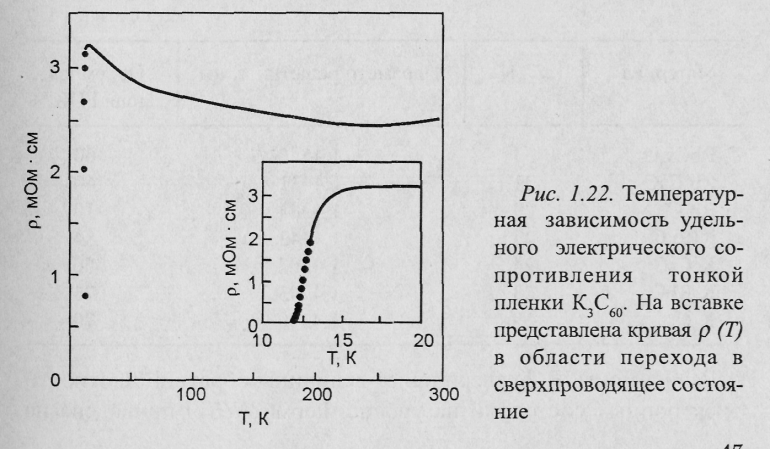
На рис. 1.22 представлена температурная зависимость удельного электрического сопротивления пленки К₃С_6О толщиной 160 нм [46].

Вблизи Тс, р = 310^-3 Омсм, что примерно на восемь порядков ниже соответствующих значений (~ 10⁵ Омсм) кристаллического С₆₀.

П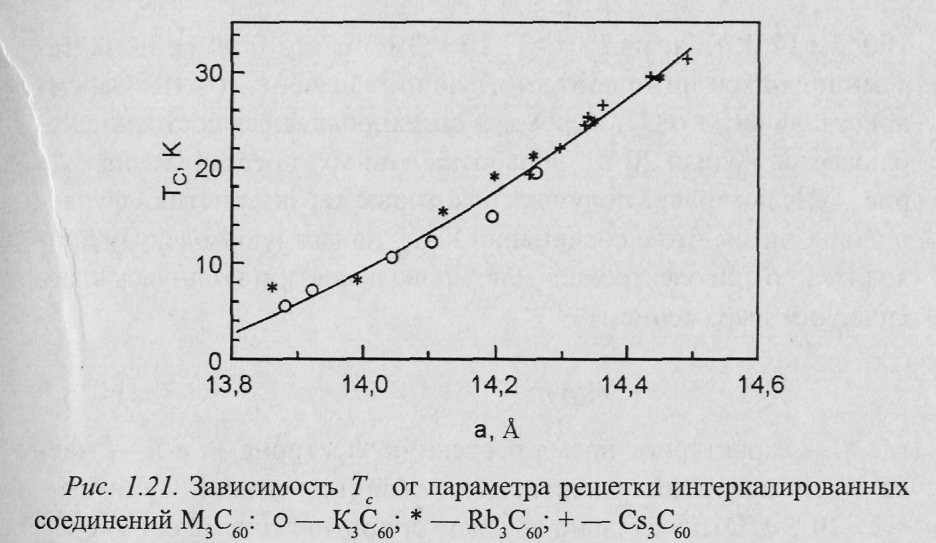 ри изучении физических свойств соединений М_хС₆₀ наибольшее внимание уделялось сверхпроводящей фазе М₃С₆₀. Обнаружено, что возрастание температуры перехода в сверхпроводящее состояние Т связано с увеличением размера атома щелочного металла. Эта закономерность приводит к почти линейной зависимости между Т. и параметром а ГЦК решетки (рис. 1.21). Чтобы объяснить полученные экспериментальные данные, нужно сделать предположение о том, что имеется слабая связь в соответствии с теорией Бардина — Купера — Шриффера (БКШ теория) и что Т. зависит только от перекрытия ближайших молекул С₆₀. При этом, однако, совершенно неясны роль и влияние легирующих элементов.

Установлено, что различные щелочные металлы в соединениях типа М₃С₆₀ подчиняются правилу спаривания электронов с участием в этом процессе фононов щелочных ионов. Также установлено, что переход изолятор — металл в легированном щелочными металлами твердом фуллерите обусловлен переходом электронов из основного состояния на более высокий уровень. Можно утверждать: соединения типа М^С^ являются молекулярными металлами для некоторых концентраций х, что объясняется большим сродством электронов С^ и низким редукционным потенциалом.

Переход в сверхпроводящее состояние наблюдается вблизи 20 К. Обработка данных, представленных на рис. 1.21, позволяет получить некоторые характеристики фуллеридов. Считая, что в соединении К^С^ на каждую молекулу приходится по три электрона в зоне проводимости и пользуясь классическим выражением

где х — характерное время рассеяния электрона, тип — масса и концентрация электронов соответственно, получим х = = 3 • 10~¹⁶ с. Относительно высокое сопротивление пленок ЬЦС^ авторы [46] связывают с мелкозернистой структурой фуллерида (d = 6—8 нм), что приводит к заниженным значениям времени рассеяния электрона.

В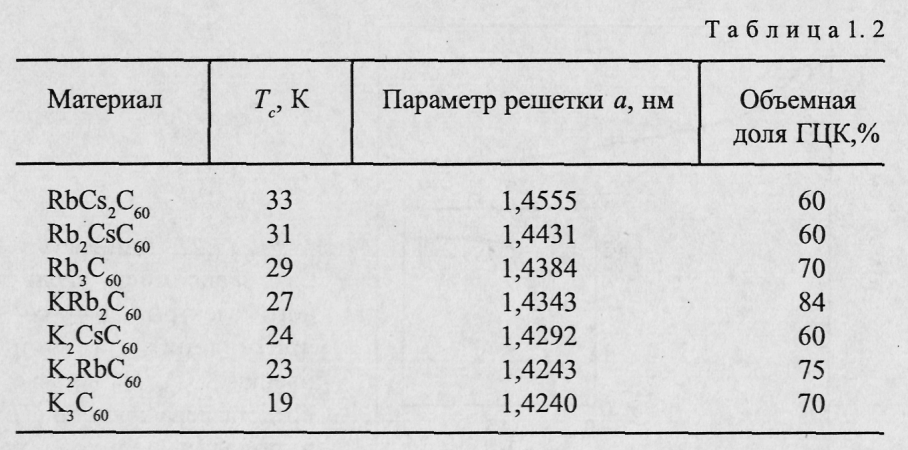 скоре было установлено, что сверхпроводящими свойствами обладают не только соединения К₃С₆₀, Rb₃C₆₀, но и XY₂C₆₀, где X и Y — атомы щелочных металлов. В табл. 1.2 приведены значения Тс., параметра а и доля ГЦК структуры в сверхпроводящих соединениях Х₃С₆₀ и XY₂C₆₀ [47].

Зависимость Г, фуллеридов от величины обратной плотности электронных состояний на уровне Ферми N(E_F) приведена на \ рис. 1.23 [48]. Отчетливо видна корреляция между а и 7\ Линейный характер зависимости T_c(N(E_F)) указывает на фононный механизм сверхпроводимости в фуллеридах. Согласно модельным представлениям БКШ теории, Г. выражается через параметры сверхпроводящего материала следующим образом:

Л инейная зависимость Тс от плотности електр-х состна уровне Ферми (рис 1,23) свид о том, что Сверхпроводимость фуллеридов обусловлена тем-же механизмом, что и у металлов, т.е. работает теория БКШ (Бардина — Купера — Шриффера) – происходит образование Куперовских пар при обмене электронов фононами.

Тс = exp[-VN(E_F)].

где со. — энергия фононов, участвующих в образовании электронных пар при возникновении сверхпроводимости; V — константа, характеризующая энергию электрон-фононного взаимодействия, приводящего к спариванию электронов. Линейный характер зависимости, представленной на рис. 1.23, согласуется с выражением (1.6) при условии, что энергия фононов со_ф= 300 К, а V = 0,03 эВ и не зависит от сорта легирующих атомов. Экспериментальные факты и модельные представления указывают на определяющий вклад внутримолекулярных колебаний С₆₀ в механизме спаривания электронов, ответственном за сверхпроводимость.

2.2.Химические равновесия.