4 Спонтанная поляризация Векторная сумма всех электронных и атомных дипольных моментов элементарной ячейки дипольного кристалла составляет ее электрический момент

(1.7)

Эту величину, характеризующую распределение электрических зарядов всей структуры кристалла, будем называть спонтанной поляризацией элементарной ячейки. Само название подчеркивает отличие спонтанной поляризации, существующей в кристаллах в отсутствие внешнего электрического поля, от индуцированной поляризации. Индуцированная поляризация состоит в возникновении дипольных моментов структурных элементов и их закономерной ориентации под действием приложенного к кристаллам внешнего электрического поля. Для бездипольных кристаллов р_s= 0, т.е. они принципиально не могут обладать спонтанной поляризацией. Для дипольных кристаллов имеются две возможности:

а) электронные дипольные моменты скомпенсированы и отсутствуют атомные дипольные моменты, т.е. р_s = 0;

б) электронные дипольные моменты не скомпенсированы или атомные дипольные моменты не равны нулю, или отличны от нуля и те, и другие дипольные моменты, т.е. р_s  0 .

Кристаллы, имеющие отличную от нуля спонтанную поля­ризацию, должны по своей точечной симметрии принадлежать к полярным кристаллографическим классам. В этом случае кристалл рассматривается как непрерывная анизотропная среда, так как при суммировании атомных и электронных ди­польных моментов мы отвлекаемся от конкретного располо­жения атомов в структуре, сводя начало векторов дипольных моментов в одну общую точку.

Спонтанная поляризация элементарной ячейки является микроскопическим параметром структуры кристалла и не мо­жет быть непосредственно измерена в эксперименте. Для по­лучения связи спонтанной поляризации с измеряемыми в экс­перименте макроскопическими параметрами введем величину, равную векторной сумме спонтанных поляризаций элементар­ных ячеек, находящихся в единице объема кристалла

(1.8)

где N - число элементарных ячеек в единице объема кристалла.

Определенная таким образом величина называется спонтанной поляризацией единицы объема или просто спонтанной поляри­зацией. Для большинства полярных кристаллов Р_s имеет то же направление, что и р_s элементарных ячеек. В системе СИ спонтанная поляризация измеряется в [Кл/м²].

. Количественная мера спонтанной поляризации

Для нахождения количественной меры спонтанной поляри­зации рассмотрим образец полярного кристалла, имеющего форму скошенного цилиндра длиной l и площадью торцовых граней S (рис.1.1).

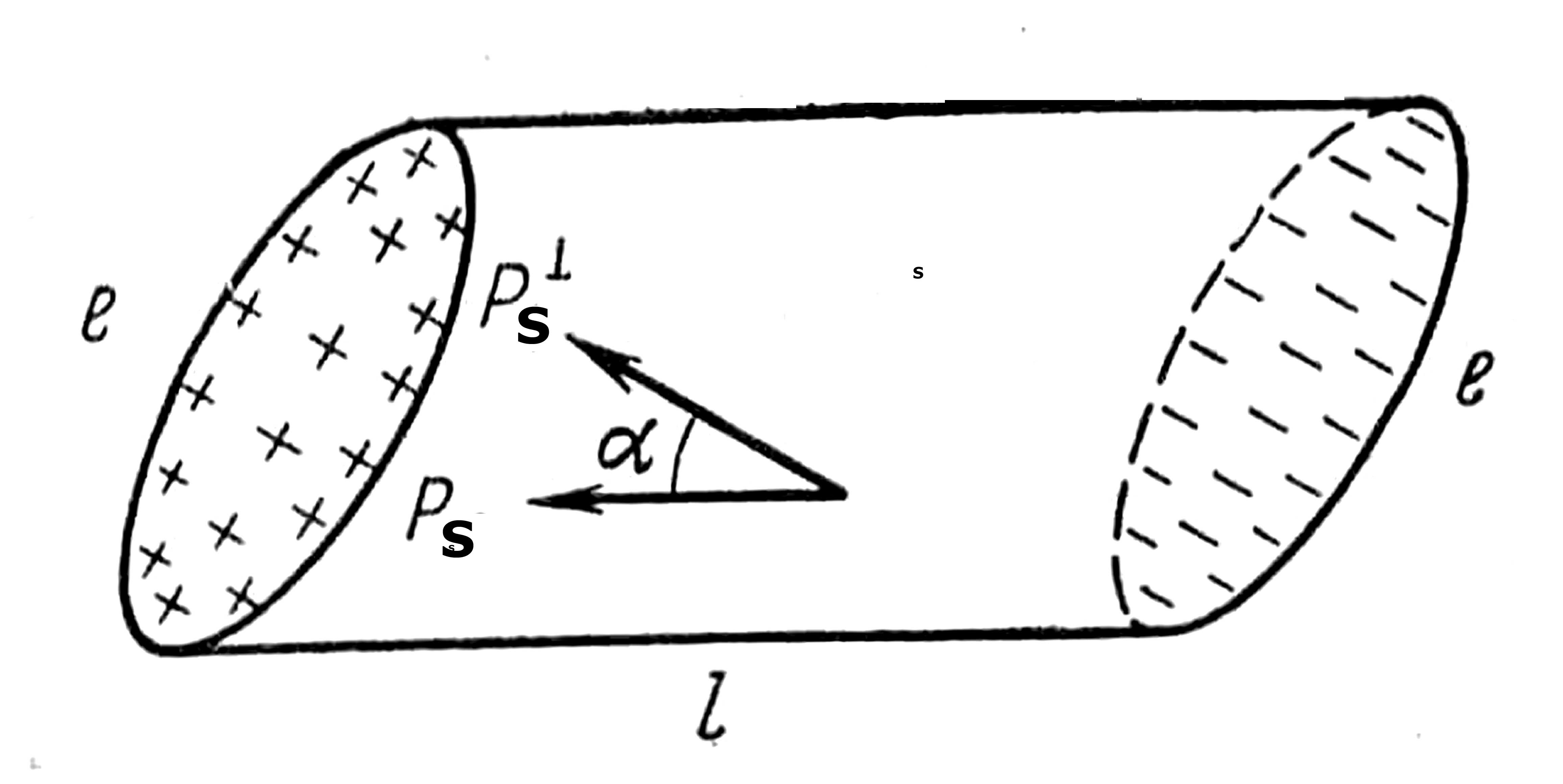
Рис. 1.1. Образец полярного кристалла с зарядами

на торцовых гранях

Пусть вектор спонтанной поляризации P_s направлен параллельно образующей цилиндра. Так как электрические центры тяжести положительных и отрицательных зарядов кристалла не совпадают, то систему диполей можно заменить одним диполем с эффективными зарядами е противоположных знаков на торцовых гранях. Очевидно, что нормальная компонента вектора спонтанной поляризации

Р_s^н = Р_s соs, (1.9)

где  - угол между Р_s и нормалью к торцовой грани. Поскольку по определению спонтанная поляризация есть дипольный момент единицы объема,

Р_s = el/V, (1.10)

где V - объем образца, то

(1.11)

В то же время поверхностная плотность зарядов торцовых граней будет

(1.12)

Сравнивая между собой последние два уравнения, получим Р_s^н = , то есть нормальная компонента спонтанной поляризации численно равна плотности зарядов на торцовых гранях. Мы получили связь между микроскопическим параметром, описывающим асимметрию распределения электрических зарядов в структуре кристалла с макроскопическим параметром – поверхностной плотностью электрических зарядов. Отсюда количественной мерой спонтанной поляризации является поверхностная плотность зарядов на гранях образца, нормальных к направлению спонтанной поляризации.

Абсолютное значение спонтанной поляризации кристаллов может быть грубо оценено из следующих простых соображений. Поскольку Р_s^н = , то в предельном случае она будет равна суммарному заряду всех электронов (или протонов), расположенных на поверхности элементарных ячеек кристалла. В простейшем случае кубической структуры достаточно рассчитать число узлов решеток N на 1 см², то есть N = 1/а², где а - параметр решетки. Принимая, например, а = 810^-8 см, получим N = 1,510¹⁴ см^-2. Поверхностная плотность заряда, определяющая предельные значения поляризации, в этом случае составит  = Р_s=Ne= 1,510¹⁴ 1,610^-19 = 25 мкКл/см². Для сравнения укажем, что в BaTiO₃ величина спонтанной поляризации составляет 26 мкКл/см².

Непосредственно обнаружить поверхностные заряды спонтанно поляризованных кристаллов можно только, если измерять возникшие на поверхностях свежего разлома заряды, прежде чем они будут скомпенсированы проводимостью и ионами воздуха. Однако и в этом случае получаются сильно заниженные значения Р_s из-за утечки заряда, неровности разлома и др. В случае линейных пироэлектриков Р_s можно измерить через пьезоэлектрический или пироэлектрический эффекты.