
Юрий Кругляк_Квантовое моделирование в квантовой химии на квантовых компьютерах_399_стр
.pdf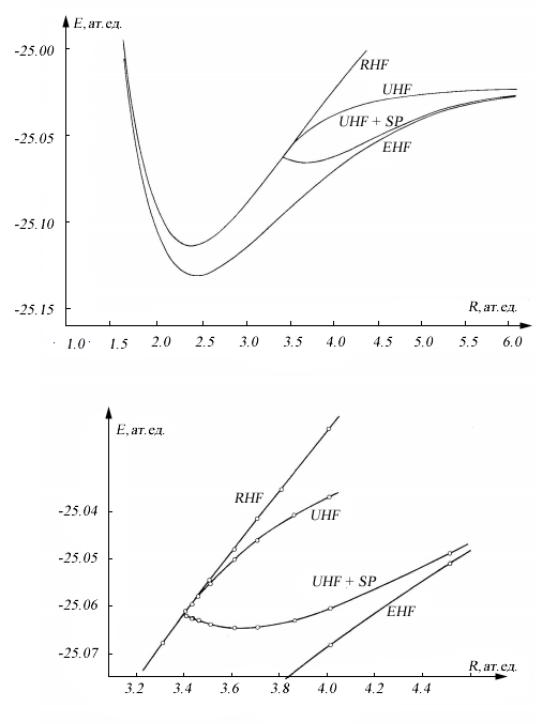
расстояниях потенциальная кривая ОХФ резко возрастает и имеет неправильную асимптотику из-за наличия ионных вкладов.
Рис. 4. Потенциальные кривые молекулы BH, полученные разными вариантами обобщенного метода ХФ [53].
Как и в этом расчете [53], стандартный метод НХФ/UHF не приводит к решению, отличному от ОХФ как при равновесном расстоянии, так и при несколько бóльших расстояниях, а в этом расчете вплоть до R ≈ 3.4 ат.ед. В этой
60
области на потенциальной кривой есть точка бифуркации, в которой возникает нетривиальное новое решение НХФ, и потенциальная кривая НХФ плавно отходит от кривой ОХФ. В этой точке бифуркации решения ОХФ и НХФ совпадают [53]. Далее кривая НХФ стремится к качественно правильному диссоциационному пределу. Заметим только, что она приближается к асимптотическому значению энергии слишком быстро, если сравнивать ее поведение с ходом асимптотики в расширенном методе ХФ (РХФ/EHF).
Волновая функция в результате спинового проектирования исходного детерминанта НХФ (НХФ-СП/UHF-SP) уже не является однодетерминантной. В результате спинового проектирования получается не только чистая спиновая функция, но и как правило наблюдается понижение энергии системы по сравнению с энергией НХФ, как это имеет место в рассматриваемом примере (рис. 4: кривая UHF-SP: область R > 3.4 ат. ед.). Это происходит только в тех областях потенциальной энергии, где реализуются настоящие решения НХФ (рис. 4: кривая UHF после R > 3.4 ат. ед.), отличающиеся от решений НХФ-СП, соответствующих чистому синглету (рис. 4: кривая UHF-SP после R > 3.4 ат. ед.). Причиной такого поведения является то, что вариационным путем оптимизируется не чистая по спину компонента волновой функции, полученная спиновым проектированием, а однодетерминантная волновая
функция, которая была у нас перед этим (метод НХФ с последующ |
им |
спиновым проектированием). |
|
Более последовательным было бы варьирование самого |
спин- |
спроектированного детерминанта в качестве вариационной пробной волновой функции (варьирование после проектирования). Эта процедура приводит к спин-спроектированному расширенному методу ХФ (РХФ/EHF). Как видим из рис. 4, метод РХФ дает качественно правильное описание гомолитической диссоциации химической связи В–Н.
Важной особенностью спин-спроектированных волновых функций является то обстоятельство, что они хорошо описывают электронную структуру антиферромагнитных систем, представляющих собой совокупность спинов, направленных то вверх, то вниз, и состоящих из двух подрешеток наивысшего возможного спина, которые вместе образуют синглет.
Волновая функция ОХФ есть частное решение уравнений РХФ, однако, в отличие от случая НХФ, решение РХФ с энергией меньше, чем энергия ОХФ, существует всюду (рис. 4). Метод РХФ можно рассматривать как расширенную одноэлектронную модель, поскольку исходный определитель РОРС содержит столько же спин-орбиталей, сколько имеется электронов в системе.
61
Были предложены упрощенные варианты метода РХФ. Например, используется только один сомножитель в (163), соответствующий наинизшей и, как правило, наибольшей по весу нежелательной спиновой компоненте. В полуспроектированном варианте метода РХФ волновая функция берется в виде суммы или разности лишь двух определителей, отличающихся друг от друга перестановкой всех спин-функций α и β . Такая волновая функция содержит только каждую вторую спиновую компоненту, например, синглет, квинтет и т.д., но не триплет, септет и т.д., и представляет собой почти чистое по спину состояние.
1.3.6.5. Метод Хартри – Фока – Рутана
Уравнения Хартри – Фока представляют собой систему связанных интегро-дифференциальных уравнений, которые в случае свободных атомов и простейших молекул решаются численными методами. Применительно к произвольным молекулярным системам решение этих уравнений в виде одноэлектронных орбиталей приходится аппроксимировать конечной линейной комбинацией (ЛК) некоторых заранее выбранных базисных функций (базисных орбиталей). Их обычно, но не обязательно, связывают с отдельными атомами в молекуле (атомные орбитали, АО). Отсюда аббревиатура ЛКАО.
Итак, разлагаем одноэлектронные орбитали ϕi по конечному базису {χµ}:
m |
|
ϕi = ∑cµi χµ, (i =1,2,3,...,m) |
(166) |
µ=1 |
|
где коэффициенты cµi каждой молекулярной орбитали (МО) ϕi |
образуют |
вектор-столбец ci . Базисные функции χµ обычно, но совсем не обязательно,
нормированы на единицу. Как правило, они не ортогональны друг к другу, но должны быть линейно независимыми.
При использовании ограниченного базиса интегро-дифференциальные уравнения ХФ сводятся к матричным уравнениям на псевдособственные значения. Они были выведены Рутаном [54] и Холлом [55] независимо друг от друга и получили название уравнений Хартри – Фока – Рутана (ХФР).
Для вывода уравнений ХФР воспользуемся теоремой Бриллюэна (§ 1.3.6.1) для однодетерминантной волновой функции, а именно:
ˆ |
(167) |
Ψ1(ϕi →ϕi′) | H | Ψ = 0, (i =1,2,3,...,n) |
|
62 |
|
где ϕi′ ортогональна всем n занятым орбиталям
ϕi′|ϕj = 0, ( j =1,2,3,...,n) , |
(168) |
и, как и ϕi , должна представляться в виде разложения по базисным функциям:
m
ϕi′= ∑qµχµ, (169)
µ=1
где на коэффициенты разложения qµ накладывается условие ортогональности
(168).
Наиболее общая произвольная орбиталь вида (169), удовлетворяющая условиям ортогональности, строится следующим образом [26].
Рассмотрим оператор проектирования на подпространство занятых орбиталей:
m
Pˆ = ∑|ϕj ϕj |. (170)
j=1
Оператор 1− P |
проектирует на ортогональное |
дополнение к этому |
ˆ |
т. е. произвольная функция |
|ϕi′ = (1− P) | ∑pν χν с |
подпространству, |
||
|
|
ˆ |
|
|
ν |
произвольными коэффициентами pν ортогональна ко всем занятым орбиталям. Коэффициенты pν произвольны и независимы друг от друга. Мы можем,
например, предположить, что для каждой вариации только один из коэффициентов отличен от нуля. Необходимо потребовать выполнение теоремы Бриллюэна для каждой функции вида:
|ϕi′ = (1 |
ˆ |
(171) |
− P) | χν . (ν =1,2,3,...,m). |
||
Выражение теоремы Бриллюэна через одноэлектронные орбитали |
||
приводит к равенству: |
|
|
|
ˆ |
(172) |
|
ϕi′| F |ϕi = 0, |
|
где оператор Фока строится из орбиталей, которые можно разложить по данному одноэлектронному базису. Взяв функцию, сопряженную к (171), получаем:
† |
=[|(1 |
ˆ |
† |
= χν |(1 |
ˆ |
(173) |
ϕi′|=[|ϕi′ ] |
− P) | χν ] |
− P) . |
||||
Подставим (173) в (172) и используем (170), а именно:
63
χν |(1 |
ˆ ˆ |
ˆ |
|
m |
ˆ |
|
|
|
|
||||
− P)F |ϕi = χν | F |ϕi − χν | ∑|ϕj ϕj |F |ϕi = |
|
|||||
|
|
|
|
j=1 |
|
(174) |
ˆ |
m |
|
ˆ |
|
m |
|
|
|
|
||||
|
|
|
∑|ϕj εiδij = 0, |
|||
= χν | F |ϕi − χν | ∑|ϕj ε ji = χν | F |ϕi − χν | |
||||||
|
j=1 |
|
|
j=1 |
|
|
так что |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
(175) |
|
χν | F |ϕi =εi χν |ϕi . |
|
||||
Остается в полученное равенство подставить (166), ввести обозначения |
||||||
|
|
ˆ |
|
, |
|
|
|
|
χν | F | χµ ≡ Fνµ |
|
(176) |
||
|
|
χν | χµ ≡ Sνµ, |
|
|||
|
|
|
|
|||
и мы окончательно получаем уравнения ХФР в развернутом виде |
|
|||||
|
m |
m |
|
|
|
|
|
∑Fνµcµi |
=εi ∑Sνµcµi |
(i = |
1,2,3,...,m) |
(177) |
|
|
µ=1 |
µ=1 |
|
|
|
|
или в матричной записи через матрицы m ×m |
|
|
|
|||
|
|
Fci =εiSci |
|
|
(178) |
|
или через полные |
матрицы |
C , столбцами |
которой |
являются |
векторы ci , |
|
а именно: |
|
FC = SCε, |
|
|
|
|
|
|
|
|
(179) |
||
где матрица ε является диагональной матрицей орбитальных энергий. Если в |
||
матрице C учитываются как занятые, так и виртуальные орбитали, тогда |
||
матрицы C и ε имеют форму m ×m . Если ограничиться учетом только занятых |
||
орбиталей, тогда матрица C имеет прямоугольную форму m ×n , |
а матрица ε |
– |
квадратную форму n ×n . |
|
|
По мере увеличения числа базисных функций энергия рассматриваемой |
||
молекулярной системы приближается к своему ХФ пределу [56]. |
|
|
1.3.6.5.1. Матрица плотности |
|
|
Рассмотрим занятые орбитали ϕi (i =1,2,3,...,n) и запишем |
оператор |
ˆ |
P |
||
проектирования на занятое подпространство через коэффициенты ЛКАО в
(166):
|
n |
n m |
m |
m n |
|
m |
P = ∑|ϕi ϕi | = ∑∑|cµi χµ ∑cνi χν | = |
∑ ∑cµicνi | χµ χν | = |
∑ Pµν | χµ χν |, (180) |
||||
ˆ |
|
|
|
|
|
|
|
i=1 |
i=1 µ=1 |
ν=1 |
µ,ν=1 i=1 |
|
µ,ν=1 |
|
|
|
|
64 |
|
|
где матрица плотности
n
Pµν = ∑cµicνi (181)
i=1
или в матричных обозначениях в виде суммы диадных произведений
n
P = ∑cici† . (182)
i=1
В случае замкнутой оболочки применительно к ОХФ матрицу плотности еще записывают как
n |
|
D = 2P = 2∑cici† . |
(183) |
i=1 |
|
Матрица P является полноценной проектирующей (на подпространство занятых орбиталей) матрицей только в том случае, если базисные функции {χµ}
ортонормированы. В общем же случае, когда Sµν = χµ | χν ≠ δµν , матрица
плотности эрмитова, но не идемпотентна, а свойством идемпотентности обладает матрица PS = (PS)2 . Действительно,
|
n |
n |
n |
n |
n |
(PS)2 |
= PSPS = ∑cici†S∑cjc†j |
S = ∑cici†Scjc†j |
S = ∑ciδijc†j |
S = ∑cici†S = PS , (184) |
|
|
i=1 |
j=1 |
i, j=1 |
i, j=1 |
i=1 |
где мы учли, что занятые орбитали ортонормированны:
m |
m |
m |
=ci†Scj =δij. |
|
|
ϕi |ϕj = ∑cµiχµ |∑cνiχν = ∑ cµiSµνcν j |
(185) |
||||
µ=1 |
ν=1 |
µ,ν |
=1 |
|
|
Умножая обе стороны равенства |
PSPS = PS |
справа на матрицу S−1 , |
которая |
||
существует, поскольку невырождена, имеем иную запись идемпотентности в форме PSP = P . Поскольку матрица S в ортонормированном базисе равна единичной матрице, то матрица P в этом случае сама является идемпотентной проектирующей матрицей.
В методе НХФ вводят две матрицы плотности: одну для орбиталей со
спином α , а другую для орбиталей |
со |
спином β . |
Пусть коэффициенты |
|
разложения для орбиталей | ai |
и |
| bi |
задаются |
векторами ai и bi , |
соответственно: |
|
|
|
|
m |
|
|
m |
|
|ai = ∑aµi |
|χµ , |
|bi = ∑bµi |χµ , |
(186) |
|
µ=1 |
|
|
µ=1 |
|
|
65 |
|
|
|
тогда
|
n |
n |
|
Pµνa |
= ∑a aµiaνi , |
Pµνb = ∑b bµibνi |
(187) |
|
i=1 |
i=1 |
|
или в матричной записи
n |
n |
|
Pa = ∑a aiai†, |
Pb = ∑b bibi† . |
(188) |
i=1 |
i=1 |
|
1.3.6.5.2. Матрица Фока и энергия
Сначала рассмотрим случай ОХФ. Элементы матрицы Фока в (177)
ˆ |
|
ˆ |
n |
ˆ |
ˆ |
χµ |
|
n |
ˆ |
|
ˆ |
|
|
|
|
|
|
|
|
|
|||||||
Fνµ = χν | F | χµ |
= χν | h + |
∑(2Ji |
− Ki ) | |
= hνµ + ∑(2 χν | Ji | χµ − χν | Ki | χµ ) .(189) |
|||||||||
|
|
|
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
Кулоновский матричный элемент, согласно (139), |
|
|
|
||||||||||
χν | Jˆi | χµ = ∫χν (1)(∫ϕi (2)r12−1ϕi (2)dv2 )χµ(1)dv1 = |
|
|
|
||||||||||
|
= ∫∫χν (1) |
|
m |
|
|
|
|
m |
(2) χµ(1)dv1dv2 |
|
|
||
|
|
∑cρi χρ (2) |
r12−1 |
∑cτi χτ |
= |
(190) |
|||||||
|
|
|
|
ρ=1 |
|
|
|
|
τ=1 |
|
|
|
|
m |
∫∫ |
|
|
|
|
|
|
|
|
m |
[χν χρ |
| χµχτ ]. |
|
ρ,τ=1 |
|
|
|
|
|
|
|
|
ρ,τ=1 |
|
|||
= ∑ cρicτi |
|
χν (1)χρ (2)r12−1χµ(1)χτ (2)dv1dv2 = ∑ cρicτi |
|
||||||||||
Аналогично, согласно (76), переписывается обменный матричный элемент:
m
χν | Kˆi | χµ = ∑ cρicτi[χν χρ | χτ χµ ]. . (191) ρ,τ=1
Подставляем (190) и (191) в (189) и пользуемся (181), тогда
Fνµ = hνµ + |
n |
|
2 |
m |
c c |
[χν χρ | χµχτ ]− |
m |
c c |
[ |
|
|
|
|
∑ |
∑ |
χν χρ | χτ χµ ] |
= |
||||||
|
∑ |
|
ρi τi |
|
ρi τi |
|
|
(192) |
|||
|
i=1 |
|
|
ρ,τ=1 |
|
|
ρ,τ=1 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
= hνµ + ∑ Pτρ (2[χν χρ | χµχτ ]−[χν χρ | χτ χµ ]), |
|
|
|||||||||
|
ρ,τ |
=1 |
|
|
|
|
|
|
|
|
|
откуда видно, что для вычисления элементов матрицы Фока нужны матрица плотности P , одно- и двухэлектронные интегралы.
66
Для метода НХФ аналогичные выкладки дают
|
m |
|
Fνµa |
= hνµ + ∑ |
(Pτρa + Pτρb )[χν χρ | χµχτ ]− Pτρa [χν χρ | χτ χµ ] , |
|
ρ,τ=1 |
(193) |
|
m |
|
Fνµb |
= hνµ + ∑ |
(Pτρa + Pτρb )[χν χρ | χµχτ ]− Pτρb [χν χρ | χτ χµ ] . |
|
ρ,τ=1 |
|
Несколько слов об обозначении двухэлектронных интегралов и их симметрии. Для интегралов
[χµχν | χρ χτ ] ≡ χµ(1)χν (2) | r−1 |
| χρ (1)χτ (2) |
(194) |
12 |
|
|
удобно использовать обозначение [12|34], поскольку оно позволяет различать сомножители из бра-скобки и из кет-скобки. Если же используются вещественные орбитали, как это обычно имеет место при выполнении вычислений на компьютерах, тогда двухэлектронные интегралы удобнее обозначать (11|22), а именно:
(χµχν | χρ χτ ) ≡ ∫∫χµ(1)χν (1)r12−1χρ (2)χτ (2)dv1dv2 =[χµχρ | χν χτ ]. |
(195) |
Из определения (195) очевидна инвариантность такой записи по отношению к перестановкам орбиталей χµ с χν и χρ с χτ , а также двух наборов
орбиталей, соответствующих переменным интегрирования 1 и 2. Обозначая для краткости (χµ χν | χρ χτ ) , как (µν | ρτ) , имеем равенства:
(µν | ρτ) = (νµ | ρτ) = (µν |τρ) = (νµ |τρ) = (ρτ | µν) = (ρτ |νµ) = (τρ | µν) = (τρ |νµ). (196)
Эту симметрию можно почувствовать, если рассматривать интеграл (195) как электростатическое взаимодействие двух зарядовых плотностей χµ (r1)χν (r1) и
χρ (r2 )χτ (r2 ) .
Всоответствии с цепочкой равенств (196), если все четыре индекса различны, то существует восемь интегралов, порядок индексов у которых в определении (195) различен, но значения их равны. При одной паре совпадающих индексов это число уменьшается до четырех, а при двух совпадающих парах – до двух, и до единицы, если все индексы одинаковы.
Используя элементы матрицы плотности D (183), а также обозначения (195), элементы фоковской матрицы в методе ОХФ вместо (192) записываются как:
m |
1 |
|
|
Fνµ = hνµ + ∑ Dτρ[(χν χµ | χρ χτ ) − |
(χν χρ | χµχτ )], |
(197) |
|
ρ,τ=1 |
2 |
|
|
67
которое можно получить из его аналога (193) для метода НХФ если учесть, что в случае ОХФ
Pa = Pb = 1 D . |
(198) |
2 |
|
Электронную энергию однодетерминантной функции в случае НХФ, согласно (158), можно записать следующим образом:
|
|
1 |
na |
|
m |
|
µi |
ˆ ˆ a |
|
m |
|
νi |
|
nb |
|
|
m |
µi |
|
|
ˆ |
ˆ b |
|
m |
|
|
|
|
|
|
|
|
|
||
E = |
2 |
|
∑ |
|
∑ |
a |
χµ |h + F |
∑ |
|
χν + |
∑ |
|
∑ |
χµ |
|h |
+ F |
∑ νi |
χν |
|
= |
|
|
|||||||||||||
|
|
|
|
|
| |
|
a |
|
|
|
b |
| |
|
|
b |
|
|
|
|||||||||||||||||
|
|
|
i=1 µ=1 |
|
|
|
ν=1 |
|
|
|
i=1 µ=1 |
|
|
|
|
|
ν=1 |
|
|
|
|
|
|
|
|||||||||||
|
= |
1 |
|
na |
|
m |
|
|
ˆ |
|
ˆ a |
|
nb |
m |
|
|
|
|
|
ˆ |
ˆ b |
|
|
|
= |
|
|
|
|
|
(199) |
||||
|
2 |
|
∑ ∑ aµiaνi χµ |h + F |
|
|χν +∑ ∑ bµibνi χµ |
|h + F |
|
|χν |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 µ,ν=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i=1 µ,ν=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
1 m |
|
a |
|
|
a |
b |
|
|
|
b |
|
= |
1 |
|
|
a |
(h + F |
a |
|
+Tr |
|
|
b |
(h + F |
b |
|
||||||||
2 µ∑,ν=1 Pµν (hµν |
+ Fµν ) + Pµν (hµν |
+ Fµν ) |
2{Tr P |
|
|
) |
P |
|
|
|
) }. |
||||||||||||||||||||||||
|
|
|
В случае ОХФ выражение для энергии упрощается до |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = 1 Tr[D(h + F )]. |
|
|
|
|
|
|
|
|
|
|
|
|
(200) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя выражения для элементов матрицы Фока (197) в ( 200), получаем электронную энергию в виде
m |
1 |
m |
|
|
1 Dρν Dτµ )(χν χµ | χρ χτ ) , |
|
E = ∑ Dµν hνµ + |
∑ |
(Dµν Dτρ − |
(201) |
|||
µ,ν=1 |
2 |
µ,ν,ρ |
,τ=1 |
|
2 |
|
в котором последнее слагаемое в обменной части матрицы Фока получено перестановкой индексов µ и ρ .
1.3.7. Корреляция электронов
Метод ХФ учитывает взаимодействие между электронами усредненным образом, а хартри-фоковские волновые функции далеки от точных решений молекулярного уравнения Шредингера. Они не учитывают то обстоятельство, что движение электронов скоррелировано, что электроны не движутся независимо друг от друга. Фактически волновая функция должна зависеть от межэлектронных расстояний.
Представить это себе можно так. Если p1(r1) есть плотность вероятности найти электрон № 1 в точке r1 независимо от положения остальных электронов, а для электрона № 2 такая плотность вероятности равна p2 (r2 ) , то для плотности вероятности p12 (r1,r2 ) того, что электрон № 1 будет найден в точке r1 и
68
одновременно электрон № 2 будет найден в точке r2 , должно иметь место неравенство
p12(r1,r2 ) ≠ p1(r1) p2(r2 ) , |
(202) |
как очевидное для статистически зависимых событий.
Движение ансамбля электронов совершенно независимо друг от друга реализуется только в приближении Хартри, когда волновая функция берется в виде простого произведения спин-орбиталей и не учитывается антисимметрия электронов как тождественных частиц. Антисимметризация волновой функции исключает возможность обнаружить два электрона с одинаковыми спинами с одной и той же точке пространства. В алгебре определителей такой детерминант автоматически обращается в нуль. С другой стороны волновая функция должна быть непрерывной. С учетом этого обстоятельства можно утверждать, что вероятность того, что два электрона с одним и тем же спином окажутся близко друг к другу мала. Эта характерная особенность распределения электронов получила название фермиевской дырки. Причиной ее появления является антисимметрия волновой функции, и ферми-дырка реализуется даже в системе невзаимодействующих электронов как чисто кинематический эффект.
В методе ХФ нескоррелировано только движение электронов с противоположными спинами. В силу исключительной практической важности классического метода Хартри – Фока корреляционную энергию определяют как разницу между хартри-фоковской энергией электронной системы и ее точным нерелятивистким значением. Согласно этому общепринятому определению, электронная корреляция включает только те эффекты, которые не являются следствием одной лишь антисимметрии и поэтому не учитываются в методе ОХФ. По другому можно сказать так. Под электронной корреляцией понимаются лишь эффекты, возникающие вследствие кулоновского отталкивания между электронами, которое и является причиной возникновения кулоновской дырки. Таким образом, электронная корреляция является динамическим эффектом, не связанным со спином в отличие от фермиевской дырки, являющейся кинематическим эффектом, зависящим от спина.
Иногда пользуются понятиями статической и динамической корреляции электронов, физический смысл которых трудно четко сформулировать. Динамическая корреляция, как прямое следствие кулоновского отталкивания между электронами, преобладает вблизи равновесных конфигураций молекул. Корреляцию считают статической тогда, когда описание с помощью однодетерминантной волновой функции в методе ОХФ, построенной из
69
