1.5. «Обратная» модель прямолинейной связи

Пусть наша задача состоит в оценивании модели прямолинейной связи между некоторыми переменными и на основе наблюденийn парзначений этих переменных. Мы уже рассмотрели вопрос об оценивании параметров такой связи, исходя из модели наблюдений. Что изменится, если мы будем исходить из «обратной» модели?

Пусть — оценки параметров и в модели наблюдений, а— оценки параметров в модели наблюдений. Тогда

т. е.

или

В то же время, по первой модели наблюдений мы получаем наилучшую прямую

а по второй — прямую

Первую прямую мы можем записать в виде

Сравнивая коэффициенты при в двух последних уравнениях, находим, что эти коэффициенты равныв том и только в том случае, когда выполнено соотношение

т. е.

или, с учетом предыдущего, когда.

Что касается отрезков на осях, то они будут совпадать тогда и только тогда, когда

или

Но

так что

При получаем

В то же время,

так что при совпадают и отрезки на осях, т. е. наилучшая прямаяодна и та жепри обеих моделях наблюдений, и это есть прямая, на которой расположенывсенаблюдаемые точки

Иными словами, наилучшие прямые, построенные по двум альтернативным моделям, совпадают в том и только в том случае, когда всеточки, расположены на одной прямой (так что); при этом,. В противном случае,и подобранные «наилучшие» прямые имеютразные угловые коэффициенты.

Кстати, в рассмотренном нами примере с уровнями безработицы, диаграмма рассеяния с переставленнымиосями (соответствующими модели наблюдений) имеет вид

Рис. 5

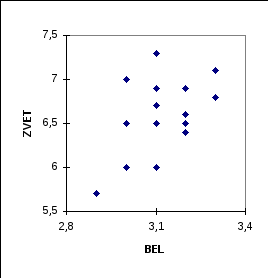
Количество точек с совпадающими знаками отклонений координат от средних значений равно 10 (4+ 6, с учетом совпадений), а число точек с противоположными знаками отклонений координат от средних значений равно 7 (4+3, с учетом совпадений). Соответственно, «облако точек» имеет некоторую вытянутость вдоль наклонной прямой, проведенной через «центр» облака. «Наилучшая» прямая имеет вид

коэффициент детерминации равен

Произведение угловых коэффициентов 0.125265 и 1.695402 наилучших прямых в «прямой» и «обратной» моделях наблюдений равно 0.212374 и совпадает со значением R².

Отметим, что несовпадение наилучших прямых, конечно, связано с тем, что в этих двух альтернативных моделях наблюдений мы минимизировали различные суммы квадратов: в «прямой» модели мы минимизировали сумму квадратов отклонений точек от подбираемой прямой в направлении, параллельном оси, а во втором — в направлении, параллельном оси.

1.6. Пропорциональная связь между переменными

Хотя на практике не рекомендуется отказываться от включения свободного члена в уравнение подбираемой прямолинейной связи, если только его отсутствие не обосновывается надежной теорией (как в физике — закон Ома), мы все же иногда сталкиваемся с необходимостью подбора прямой, проходящей через начало координат. Позднее мы приведем соответствующие примеры.

Итак, пусть мы имеем наблюдения , и предполагаем, что гипотетическая линейная связь между переменными иимеет вид

(пропорциональная связь между переменными), так что ей соответствует модель наблюдений

.

Применение метода наименьших квадратов в этой ситуации сводится к минимизации суммы квадратов невязок

по всем возможным значениям .Последняя сумма квадратов является функциейединственнойпеременной (при известных значениях), и точка минимума этой функции легко находится. Для этого мы приравниваем нулю производнуюпо:

(нормальное уравнение)

откуда получаем:

или

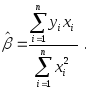
Отсюда видно, что при таком подборе

и точка ужене лежит, как правило, на подобранной прямой

Более того, в такой ситуации

где

и поэтому использовать для вычисления коэффициента детерминации выражение

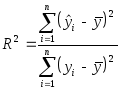
не имеет смысла. В этой связи полезно рассмотреть следующий искусственный пример.

Пример

Пусть переменные и принимают в четырех наблюдениях значения, приведенные в следующей таблице

i	1	2	3	4
xi	10	3	–10	-3
yi	11	3	-9	-3

соответствующей диаграмме рассеяния

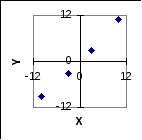
и мы предполагаем пропорциональнуюсвязь между этими переменными, что соответствует модели наблюденийДля этих данных

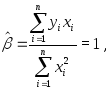
так что При этом,

RSS = (11—10)²+ (3-3)²+ (-9+10)²+ (-3+3)²= 2,

TSS = (11-0.5)²+ (3-0.5)²+ (-9-0.5)²+ (-3-0.5)²= 219,

ESS = (10-0.5)²+ (3-0.5)²+ (-10-0.5)²+ (-3-0.5)²= 219,

так что здесь , и вычислениепо формуле

приводит к значению . Но последнее возможно только если все точкилежат на одной прямой, а у нас это не так. Заметим также, что в этом примере сумма остатков, что невозможно в модели с включением в правую часть постоянной составляющей.

Можно, конечно, попытаться справиться с возникающим при оценивании модели без постоянной составляющей затруднением, попросту игнорируянарушение соотношенияи определяя коэффициент детерминации соотношением

,

и именно такое значение приводится в протоколах некоторых пакетов программ анализа статистических данных, например пакета ECONOMETRIC VIEWS (TSP). Для нашего иллюстративного примера с четырьмя наблюдениями использование последнего приводит к значению, которое не противоречит интуиции и представляется разумным. Однако, к сожалению, и такой подход к определению коэффициента детерминации не решает проблемы, поскольку, в принципе, при оценивании модели без постоянной составляющей возможны ситуации, когда, что приводит котрицательнымзначениям.

Пример

Пусть переменные и принимают в четырех наблюдениях значения, приведенные в следующей таблице

i	1	2	3	4
xi	0	0.2	0.4	3
yi	0.5	0.8	1.2	2

что соответствует диаграмме рассеяния

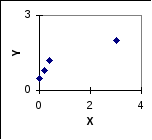
и мы предполагаем пропорциональную связь между этими переменными, что соответствует модели наблюдений Для этих данных. При этом,,, и вычислениепо формуле приводит котрицательномузначению

Преодолеть возникающие затруднения можно, если определить в модели наблюдений без постоянной составляющей формулой

,

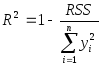в которой используется сумма квадратов нецентрированныхзначений переменной(отклонений значений переменнойот «нулевого уровня»). При таком определении, неотрицательность коэффициента гарантируетсяналичием соотношения

которое отражает геометрическуюсущность метода наименьших квадратов (аналог знаменитой теоремы Пифагора для многомерного простанства) и выполняетсякак для модели без постоянной составляющей, так и для модели с наличием постоянной составляющей в правой части модели наблюдений. Деля обе части последнего равенства наприходим к соотношению

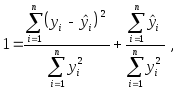
из которого непосредственно следует, что

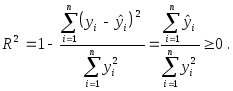
(Доказать заявленное равенство не сложно. Действительно,

Но

(см. нормальное уравнение), что и приводит к искомому результату.)

В последнем примере использование определения сне центрированными дает.