2.6. Доверительные интервалы для коэффициентов: реальные статистические данные

Итак, практическому построению доверительных интервалов для коэффициентов нормальной модели линейной множественной регрессии

с  i. i. d. препятствует вхождение в выражения для дисперсий

неизвестного значения ^.

Единственный выход из этого положения — заменить неизвестное значение  ^ какой-нибудь подходящей егооценкой (estimate), которую можно было бывычислить на основании имеющихся статистических данных. Такого рода оценки принято называтьстатистиками (statistics).

В данной ситуации такой подходящей оценкой для неизвестного значения является статистика

Поскольку сумма являетсяквадратичной функцией от случайных величин, то она является случайной величиной, а следовательно,случайной величиной является истатистика S². Математическое ожидание этой случайной величины равно :

т. е. —несмещенная оценка для .

Замечание. В частном случае модель наблюдений принимает вид

(случайная выборка из распределения N (₁,²)). Несмещенной оценкой для служит

Оценкой наименьших квадратов для параметра является, так что, и

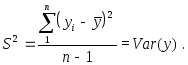
Таким образом, выборочная дисперсия переменной, получаемая делениемименно на(а не на), является несмещенной оценкой для в модели случайной выборки из нормального распределения, имеющего дисперсию . Этим и объясняется сделанный нами выбор нормировки при определении выборочных дисперсий и ковариаций.

При выполнении стандартных предположений отношение

имеет стандартное распределение, называемое распределением хи-квадрат с (n-p) степенями свободы. Такое же распределение имеет сумма квадратовслучайных величин,независимых в совокупности и имеющих одинаковое стандартное нормальное распределение. При график функции плотности этого распределения имеет вид

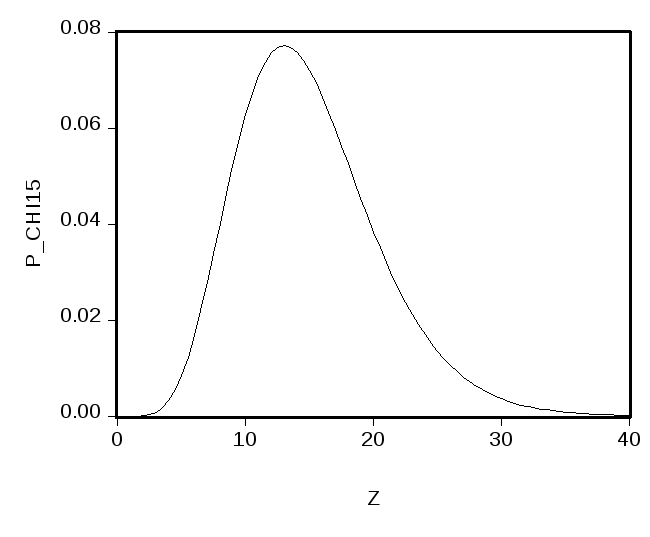
Для обозначения распределения хи-квадрат с  степенями свободы используют символ².

Итак, мы не знаем истинного значения и поэтому в попытке построить доверительный интервал длявынуждены заменить неизвестное нам значениена его несмещенную оценку

Соответственно, вместо отношения

приходится использовать отношение

Однако последнее отношение как случайная величинаужене имеет стандартного нормального распределения, поскольку в знаменателе теперь стоит не постоянная, аслучайная величина.

Тем не менее, распределение последнего отношения также относят к стандартным, и оно известно под названием t-распределения Стьюдента с (n-p) степенями свободы.

Для распределения Стьюдента с  степенями свободы принято обозначениеt (). Квантиль уровняр такого распределения будем обозначать символомt_p (K). График функции плотности распределения Стьюдента симметричен относительно нуля и похож на график функции плотности нормального распределения. Например, прион имеет следующий вид (левый график).

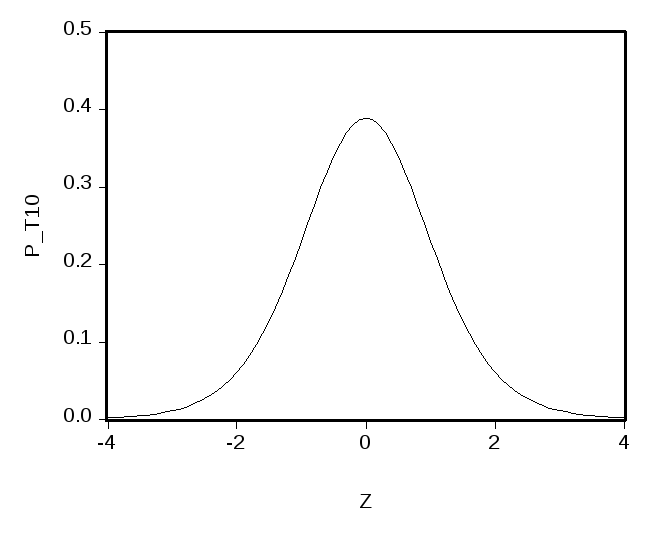
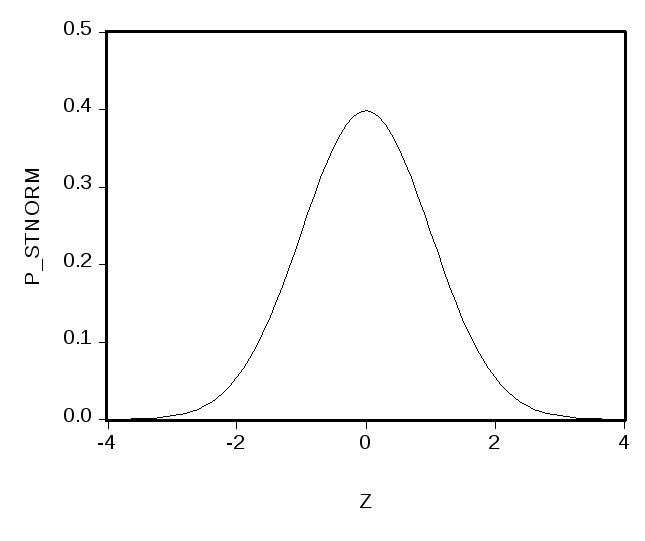
Для сравнения, справа приведен график функции стандартного нормального распределения. Отличие графиков столь невелико, что визуально они почти неразличимы. Квантили этих двух распределений различаются более ощутимо:

Распределение Стьюдента имеет более тяжелые хвосты.Из приведенных значений квантилей следует, например, что случайная величина, имеющая стандартное нормальное распределение, может превысить значение 1.645 лишь с вероятностью 0.05. В то же самое время, с такой же вероятностью 0.05 случайная величина, имеющая распределение Стьюдента с 10 степенями свободы, принимает значения, большие, чем 1.812.

Впрочем, для значений квантили распределения Стьюдента практически совпадают с соответствующими квантилями cтандартного нормального распределения .

Итак,

.

Поэтому для этой случайной величины выполняется соотношение

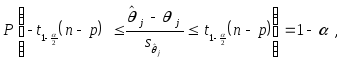
так что с вероятностью, равной , выполняется двойное неравенство

т. е.

Иными словами, с вероятностью, равной ,случайный интервал

накрывает истинное значение коэффициента  _j, т. е. является%- доверительным интервалом для  _j в случае,когда не известно истинное значение  ² дисперсии случайных ошибок.В среднем, длина такого интервала больше, чем длина доверительного интервала с тем же уровнем доверия, построенного приизвестномзначении .

Замечание. Выбор конкретного значения определяет компромисс между желанием получитьболее короткийдоверительный интервал и желанием обеспечитьболее высокийуровень доверия.

Попытка повысить уровень доверия , выраженная в выбоременьшегозначения , приводит к квантилис более высоким значением, т. е. к большему значению. Но длина доверительного интервалапропорциональна. Следовательно,увеличение уровня доверия сопровождается увеличением ширины доверительного интервала (притех жестатистических данных).

Так, для можно приближенно считать, что

,

где — квантиль уровня стандартного нормального распределения. Соответственно, выбирая уровень доверия равным  или , мы получаем длязначения, приблизительно равные. Это означает, что переход от уровня доверия к уровню доверия сопровождается увеличением длины доверительного интервала приблизительно в раза, а дополнительное повышение уровня доверия до увеличивает длину доверительного интервала еще примерно в раза.

Теперь мы в состоянии перейти к построению интервальных оценок параметров моделей линейной регрессии для различного рода социально-экономических факторов на основании соответствующих статистических данных.

Пример. Вернемся к модели зависимости уровня безработицы среди белого населения США от уровня безработицы среди цветного населения. Запишем линейную модель наблюдений в виде

Получаем: =. Коэффициентоценивается величинойдисперсияоценивается величиной. Для построения —доверительного интервала дляостается найти квантиль уровняраспределения Стьюдента сстепенями свободы. Используя, например, Таблицу А.2 из книги Доугерти (стр.368), находим:. Соответственно, получаем -доверительный интервал дляв виде

т. е.

Для имеем,; -доверительный интервал дляимеет вид

т. е.

В связи с этим примером, отметим два обстоятельства.

(а) Доверительный интервал для коэффициентадопускает какположительные, так и отрицательныезначения этого коэффициента.

(б) Каждый из двух построенных интервалов имеет уровень доверия ; однако этоне означает, что с той же вероятностью сразуоба интерваланакрывают истинные значения параметров,.

Справиться с первым затруднением в данном примере можно, понизивуровень довериядо . В этом случае в выражении для доверительного интервала квантильзаменяется на квантиль, так что левая граница доверительного интервала длястановится положительнойи равной . Однако это достигается ценой того, что новый доверительный интервал будет накрывать истинное значение параметрав среднем только в 90 случаев из 100, а не в 95 из100 случаев.

Что касается второго затруднения, то наиболее простой путь взятия под контроль вероятности одновременного накрытиядоверительными интервалами для,истинных значений этих параметров связан с тем, что

оба интервала накрывают и, соответственно=

хотя бы один из них не накрывает соответствующее =

доверительный интервал дляне накрывает+

доверительный интервал дляне накрывает

оба интервала не накрывают свои =

оба интервала не накрывают свои

Следовательно, если построить доверительный интервал дляи доверительный интервал дляс уровнями доверия каждого, равными, то тогда правая часть полученной цепочки соотношений будет равна

Это означает, что в нашем примере мы можем гарантировать, что вероятность одновременного накрытияистинных значений,соответствующими доверительными интервалами будетне менее , если возьмем. Но тогда при построении этих интервалов придется использовать вместо значения

значение

,

так что каждый из исходных интервалов увеличитсяв раза. Это, конечно, приводит к еще более неопределенным выводам относительно истинных значений параметров,.