2.4. Нормальные линейные модели с несколькими объясняющими переменными

Начиная с этого момента, мы будем предполагать, что

(1) Модель наблюдений имеет вид

где - значение объясняемой переменной в-м наблюдении;

- известное значение-ой объясняющей переменной в-м наблюдении;

- неизвестный коэффициент при-ой объясняющей переменной;

- случайная составляющая (“ошибка“) в -м наблюдении.

(2) -случайные величины,независимые в совокупности, имеющиеодинаковое нормальное распределение N (0,²)с нулевым математическим ожиданием и дисперсией

(3) Если не оговорено противное, то в число объясняющих переменныхвключается переменная, тождественно равная единице, которая объявляется первой объясняющей переменной, так что

При сделанных предположениях являютсянаблюдаемыми значенияминормально распределенных случайных величин ,которыенезависимы в совокупностии для которых

так что



В отличие от ,случайные величины имеют распределения,отличающиеся сдвигами.

Определенную указанным образом модель наблюдений мы будем называть нормальной линейной моделью с p объясняющими переменными. Иначе ее еще называютнормальной линейной моделью множественной регрессии переменной y на переменные x₁, ... , x_p . Термин “множественная” указывает на использование в правой части модели наблюденийдвух и болееобъясняющих переменных, отличных от постоянной. Термин “регрессия” имеет определенные исторические корни и используется лишь в силу традиции.

Оценивание неизвестных коэффициентов модели методом наименьших квадратов состоит в минимизации по всем возможным значениям суммы квадратов

Минимум этой суммы достигается при некотором наборе значений коэффициентов

так что

Это минимальное значение мы опять обозначаем RSS , так что

и называем остаточной суммой квадратов.

Коэффициент детерминации R² определяется как

где

Обозначая

(подобранные - fitted- значения объясняющей переменной по оцененной линейной модели связи), и определяя остаток (residual)от i-го наблюдения как

мы получаем:

Обозначая

- объясненная моделью (explained) сумма квадратов, илирегрессионная сумма квадратов, мы так же, как и в случаепростойлинейной регрессии с, имеем разложение

так что

И опять, это разложение справедливо только при наличии постоянной составляющейв модели линейной связи. При этом, также, здесь

т.е. коэффициент детерминации равен квадрату выборочного коэффициента корреляции между переменнымии. Последний называетсямножественным коэффициентом корреляции (multiple-R).

Для поиска значений ,минимизирующих сумму

следует приравнять нулю частные производные этой суммы (как функции от )по каждому из аргументов . В результате получаемсистему нормальных уравнений

или

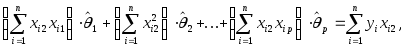
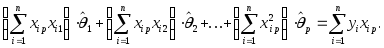
Это система линейных уравнений с неизвестными . Ее можно решать или методом подстановки или по правилу Крамера с использованием соответствующих определителей. В векторно-матричной форме эта система имеет вид

где

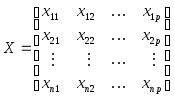
- матрица значений объясняющих переменных внаблюдениях;

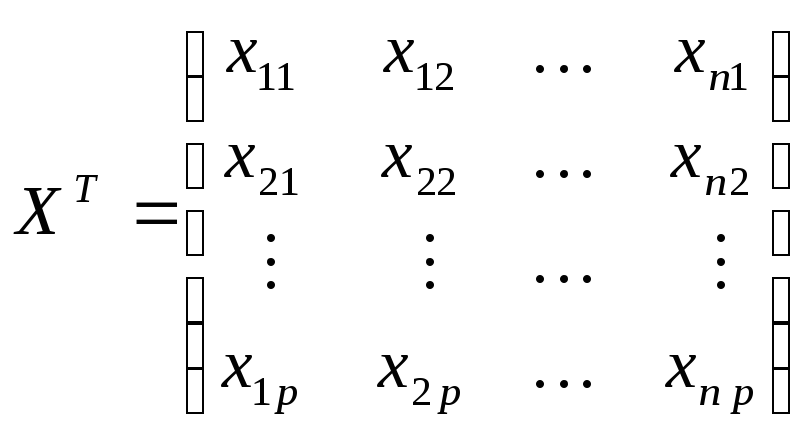
- транспонированная матрица;

и

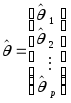
соответственно, вектор-столбец значений объясняемой переменной в наблюдениях и вектор-столбец оценокнеизвестных коэффициентов. Система нормальных уравненийимеет единственное решение, если выполнено условие

(4) матрица X^TX невырождена, т.е. ееопределитель отличен от нуля:

которое можно заменить условием

(4^’) столбцы матрицы X линейно независимы.

При выполнении этого условия матрица (размера) имеет обратную к ней матрицу. Умножая в таком случае обе части последнего уравнения слева на матрицу, находим искомое решение системы нормальных уравнений:

Введем дополнительные обозначения

, ,,.

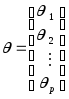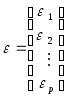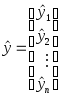Тогда модель наблюдений

можно представить в матрично-векторной форме

Вектор подобранных значений имеет вид

и вектор остатков равен

Определяющим для всего последующего является то обстоятельство, что в нормальной линейной модели с несколькими объясняющими переменными оценки коэффициентов как случайные величины имеютнормальные распределения(хотя эти случайные величины уже не являются независимыми в совокупности).

Действительно, поскольку , то оценки являютсялинейными комбинациями значений ,т.е. имеют вид

где - коэффициенты, определяемые значениями объясняющих переменных. Поскольку же у нас -наблюдаемые значения случайных величин , то являетсянаблюдаемым значением случайной величиныкоторую мы также будем обозначать :

Ранее мы выяснили, что при наших предположениях



Поэтому случайные величины также будут нормальнымикак линейные комбинации независимых нормально распределенных случайных величин.

Можно показать, что математическое ожидание случайной величиныравно

(являетсянесмещенной оценкой истинного значения коэффициента ), а дисперсия этой случайной величины равна-му диагональному элементу матрицы:

Рассмотренная ранее модель простой линейной регрессии

вкладывается в модель множественной линейной регрессии с :

, ,,.

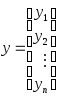Матрица имеет вид

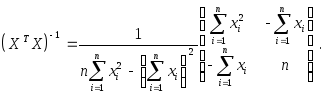
Учитывая, что

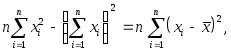
находим: