2.5. Нормальная множественная регрессия: доверительные интервалы для коэффициентов

Рассматривая нормальную модель линейной множественной регрессии

с  i. i. d. , мы установили, что оценка наименьших квадратовнеизвестного истинного значениякоэффициента при— ой объясняющей переменной имеет нормальное распределение, причем

Рассмотрим теперь случайную величину

получаемую путем вычитания из случайной величины ее математического ожидания и деления полученной разности на корень из дисперсии(т. е. путемцентрированияинормирования случайной величины). При совершении этих двух действий мы не выходим из семейства нормальных случайных величин, получая опять женормальнуюслучайную величину, но только уже с другими математическим ожиданием и дисперсией. Используя упомянутые ранее свойства математического ожидания и дисперсии, находим:

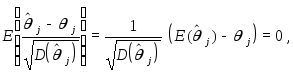
так что



Иными словами, в результате центрирования и нормирования случайной величины мы получили случайную величину, имеющуюстандартное нормальное распределение, т. е.нормальное распределение с нулевым математическим ожиданием и единичной дисперсией. Функцию распределения и функцию плотности распределения такой случайной величины обозначают, соответственно, каки:

Для каждого значения , определим символомчисло, для которого, так что если случайная величинаимеет стандартное нормальное распределение, то тогда

Такое число называется квантилью уровня p стандартного нормального распределения.

1-p

z_p

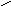
Заштрихованная площадь под графиком плотности стандартного нормального распределения находитсяправееквантилиуровня;

эта квантиль равна . Поэтому площадь под кривой, лежащаялевееточки, равна, азаштрихованная площадь равна. Последняя величина есть вероятность того,что случайная величина, имеющая стандартное нормальное распределение, примет значение,превышающее .

Если мы возьмем какое-нибудь число в пределах отдо, и выделим интервал

то получим следующую картину:

Из симметрии функции плотности нормального распределения вытекает равенство площадей областей, заштрихованных на последнем рисунке. Но площадь правой заштрихованной области равна ; следовательно, такова же и площадь левой заштрихованной области. Это, в частности, означает, что вероятность того, что случайная величинапримет значение, не превышающее, равна, так что

Часть площади под кривой стандартной нормальной плотности, лежащая в пределах выделенного интервала, меньше единицы на сумму площадей заштрихованных областей («хвостов»), т. е. равна

Эта величина равна вероятноститого, что случайная величина, имеющаястандартное нормальное распределение,примет значение в пределах указанного интервала²:

Но ранее мы установили, что стандартное нормальное распределение имеет случайная величина

Поэтому для этой случайной величины справедливо соотношение

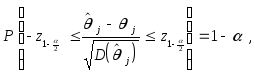
так что с вероятностью, равной , выполняется двойное неравенство

т. е.

Иными словами, с вероятностью, равной ,случайный интервал

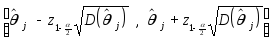
накрывает истинное значение коэффициента  _j. Такой интервал называетсядоверительным интервалом для  _j с уровнем доверия (доверительной вероятностью) , или()-доверительным интервалом, или100()-процентным доверительным интервалом для  _j.

Последний рисунок был получен при значении   .Поэтому площади заштрихованных областей («хвосты») равны , сумма этих площадей равна и площадь области под кривой в пределах интерваларавна   Остается заметить, что

так что случайный интервал

является 95%-доверительным интервалом для  _j. Егодлина

пропорциональна—среднеквадратической ошибке (среднеквадратическому отклонению) оценки коэффициента _j.

Хотелось бы, конечно, прямо сейчас построить доверительные интервалы для коэффициентов линейной модели по каким-нибудь реальным статистическим данным. Однако этому препятствует то обстоятельство, что в выражения для дисперсий

входит не известное нам значение ^.