Часть 2. Статистические выводы при стандартных предположениях о вероятностной структуре ошибок в линейной модели наблюдений

2.1. Вероятностное моделирование ошибок

Мы уже неоднократно сталкивались с вопросом о том, сколь существенно величина коэффициента корреляции (детерминации) должна отличаться от нуля, чтобы можно было говорить о действительно существующей линейной связи между исследуемыми переменными.

Если оцененноезначение эластичности потребления некоторого товара оказалось несколько больше единицы, то возникает вопрос о том, сколь надежным является заключение о том, что потребление этого товара эластично по ценам.

Если мы будем использовать подобранную прямую

для прогнозирования значений дляновыхнаблюдений, t n1,...,nk, то сколь надежными будут такие прогнозы?

Если у нас нет теоретических(экономических) оснований для выбора между моделью в уровнях переменных и моделью в логарифмах уровней, то как выбрать одну из этих моделей на основании одних только наблюдений?

Ответы на эти и другие подобные вопросы невозможны, если мы не сделаем некоторых более или менее подробных предположений о структуре последовательности ошибок , участвующих в определении модели наблюдений

Базовая, и наиболее простая модель для последовательности предполагает, что —независимые случайные величины, имеющие одинаковое распределение (i. i. d. — independent, identically distributed random variables).

Для нас (пока!) достаточно представлять случайную величину как переменную величину, такую, чтодонаблюдения ее значенияневозможно предсказать это значение абсолютно точно, и, в то же время,для любого , определенавероятность

того, что наблюдаемое значениепеременной не превзойдет ; . Функция называетсяфункцией распределения случайной величины (c. d. f. — cumulative distribution function).

Говоря об ошибках како случайных величинах, мы, соответственно, понимаем указанную линейную модель наблюдений таким образом, что

а) существует(теоретическая, объективная или в виде тенденции) линейная зависимость значений переменнойот значений переменной с вполне определенными, хотя обычно и не известными исследователю, значениями параметров и;

б) эта линейная связь для реальных статистических данных не является строгой: наблюдаемые значенияпеременной отклоняютсяот значений, указываемых моделью линейной связи

в) при заданных(известных) значениях конкретные значения отклонений

не могут быть точно предсказаныдо наблюдения значенийдаже если значения параметров иизвестны точно;

г) для каждого определена вероятностьтого, чтонаблюдаемое значениеотклоненияне превзойдет , причем эта вероятностьне зависит от номера наблюдения;

д) вероятность того, что наблюдаемое значение отклонения вi-м наблюдении не превзойдет ,не зависитот того, какие именно значения принимают отклонения в остальных наблюдениях.

В дальнейшем, говоря о той или иной случайной величине , мыбудем предполагать существованиефункции принимающей тольконеотрицательные значенияи такой, что

1) площадь под кривой

в прямоугольной системе координат (точнее, площадь, ограниченная сверху этой кривой и снизу — горизонтальной осью )равна ,

2) для любой парызначений с , вероятность

численно равна площади, ограниченной снизу осью , сверху — кривой, слева — вертикальной прямой , справа — вертикальной прямой (т. е. равначасти площади под кривой, расположенноймежду точками и ).

3) для любого , вероятность того, что наблюдаемое значение не превзойдет , равна площади, ограниченной снизу осью , сверху — кривойи справа — вертикальной прямой , т. е. равначасти площадипод кривой, расположеннойлевее точки .

Заметим, что при этом выполняется следующее важное соотношение:

(Действительно, вероятность численно равна части площади под кривой, расположеннойлевее точки , а эта часть складывается из части площади под кривой, расположеннойлевее точки и части площади под кривой, расположенноймежду точками и , так что

откуда и следует заявленное соотношение.) Кроме того,

(Действительно,

поскольку слева складываются части площади под кривой , расположенные, соответственно,левееиправееточки , так что в сумме они составляютвсюплощадь под этой кривой, а вся площадь под кривойкак раз и равна 1.)

Функция связана с функцией распределения случайной величины соотношениями

и называется функцией плотности вероятности случайной величины (p.d.f. — probability density function). Для краткости, мы часто будем говорить о функциикак офункции плотностиили оплотности распределенияслучайной величины .

Возьмем два непересекающихся интервала значений переменной :и. Рассмотрим два варианта распределения вероятности случайной величины :равномерное распределение на отрезкеитреугольное распределениена том же отрезке. Графики функций плотности для этих двух вариантов имеют следующий вид:

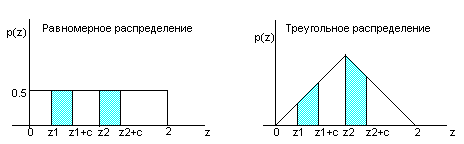
Площади заштрихованных прямоугольников на первомграфике численно равны вероятностям того, что случайная величина , имеющаяравномерноераспределение на отрезке, примет значения в пределахи, соответственно. Поскольку основания и высоты этих прямоугольников равны, то равны и их площади, т.е.равны указанные вероятности.

Площади заштрихованных трапеций на второмграфике численно равны вероятностям того, что случайная величина , имеющаятреугольноераспределение на отрезке, примет значения в пределахи, соответственно. Высоты этих трапеций равны, однако стороны трапеции, расположенной правее, больше сторон трапеции, расположенной левее. Поэтому и площадь трапеции, расположенной правее, больше площади трапеции, расположенной левее. А это означает, в свою очередь, что вероятность того, что случайная величина , имеющая треугольное распределение на отрезке, примет значения в пределах,большевероятности того, что эта случайная величина примет значения в пределах.

Таким образом, функция плотности указывает на более вероятныеименее вероятныеинтервалы значений случайной величины. Если случайная величина имеетравномерноераспределение на отрезке, то для неевсеинтервалы значений, имеющие одинаковую длину и расположенныецеликомв пределах отрезка, имеютодинаковыевероятности (т. е. вероятности попадания значений случайной величины на эти интервалы одинаковы). Если же случайная величина имееттреугольноераспределение на отрезке, то для нее интервалы значений, имеющие одинаковую длину и расположенныецеликомв пределах отрезка, имеют, вообще говоря,различныевероятности: вероятность того, что случайная величина примет значение в интервале, расположенном ближе к центральному значению,большевероятности того, что случайная величина примет значение в интервале, расположенном ближе к одному из концов отрезка.

Обсудим несколько более точно вопрос о том, что мы понимаем под независимостьюнескольких случайных величин. Пусть мы имеем случайных величин , имеющиходинаковую функцию распределения. Мы говорим, что эти случайные величинынезависимы в совокупности, еслидля любого набора пар,,...,, где и могут быть равны такжеи,

При таком предположении условная вероятность того, что, например, ,при условии, что ,, ,равнабезусловной вероятности того, что , т. е. вероятности, вычисляемойбез задания указанногоусловия:

(Вертикальная чертав этой формуле указывает на то, что первая вероятность —условная; справа от вертикальной черты записаноусловие, при котором вычисляется эта вероятность.) Иначе говоря, на распределение вероятности случайной величины не влияетинформация о значениях случайных величин. И вообще, на распределение вероятностей случайной величины не влияет информация о значениях случайных величинс.

Если случайные величины имеютодинаковое распределение(заданное или функцией распределения или функцией плотности) инезависимы в совокупности, то часто это обозначают в записи следующим образом:

.

Возвращаясь к модели наблюдений

и предполагая, что —независимые случайные величины, имеющие одинаковое распределение (i. i. d), мы должны теперь сделать еще и предположение о том,каким именноявляется это одинаковое для всех распределение.