2.3. Числовые характеристики случайных величин и их свойства

Случайные величины, с которыми мы имеем дело в данном курсе, полностью определяютсязаданием ихфункции плотности, указывающей на зоны более вероятных и менее вероятных значений случайной величины. Часто, однако, интересуются более сжатыми характеристиками распределений случайных величин, выраженнымиотдельными числами. К таким характеристикам, в первую очередь, относятсяматематическое ожидание идисперсия случайной величины.

Пусть случайная величина имеет функцию плотности. График функцииограничивает вместе с осью абсциссполосу переменной ширины. Если рассматривать эту полосу как материальный объект определенной (постоянной) толщины, изготовленный из однородного материала и имеющий массу, равную единице, то абсцисса центра тяжести этого материального объекта называетсяматематическим ожиданием (expectation)случайной величины X, обозначаетсяE (X) и вычисляется по формуле

Если график функции плотности симметричен относительно оси ординат(так что—четнаяфункция), то

Довольно часто о говорят как осреднем значении случайной величины X. Это связано с тем, что если—независимые копиислучайной величины(т. е. случайные величинынезависимы в совокупности и имеют то же распределение, что и), то тогдапри большихдлянаблюдаемыхзначенийслучайных величинимеет местоприближенное равенство

тем более точное, чем больше значение. Иными словами, с увеличениемзначениесколь угодно точно приближается значением среднеарифметического наблюдаемых величин.

Обратимся опять к упомянутому ранее гауссовскому(нормальному) распределению с функцией плотности

и пусть случайная величина имеет такое распределение с, а случайная величинаимеет такое распределение с. Сравним графики соответствующих функций плотности (сплошной линией представлен график функции плотности случайной величины):

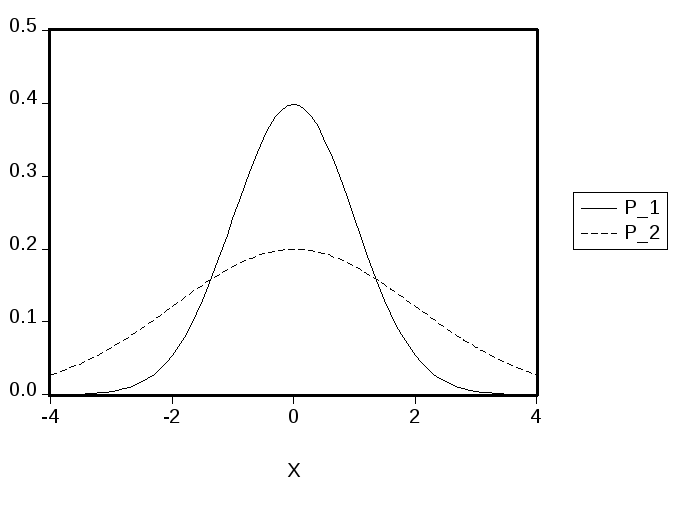
Поскольку в обоих случаях графики симметричны относительно нуля, то

т. е. математические ожиданияслучайных величинисовпадают. Однако, распределение случайной величиныболее рассредоточено, и это означает, чтодля любого

При этом говорят, что распределение случайной величиныимеетболее тяжелые (heavy), илиболее длинные(long)хвосты (tails). Соответственно,

В рассмотренном случае в качестве числовой характеристики степени рассредоточенности распределения можно было бы принять параметр: чем больше значение этого параметра, тем более рассредоточено распределение. В общем случае, сравнивать степени рассредоточенности распределений случайных величин можно, привлекая для этой цели понятиедисперсии.

Дисперсией (variance)случайной величины X называют число

равное математическому ожиданию квадрата отклонения случайной величиныот ее математического ожидания.¹Зная функцию плотностислучайной величины, дисперсию этой случайной величины можно вычислить по формуле

Таким образом, математическое ожидание можно интерпретировать каквзвешенное среднее возможных значенийслучайной величины, с весами, пропорциональными, а дисперсию— каквзвешенное среднее (с теми же весами) квадратов отклонений возможных значений случайной величиныот ее математического ожидания.

Если случайная величина имеетнормальное распределениес функцией плотности

то для нее

Таким образом, случайная величина, имеющая нормальное распределение,полностью определяется(в отношении ее распределения) заданием значений ее математического ожидания и дисперсии.

В связи с частым использованием нормально распределенных случайных величин в дальнейшем изложении, мы будем обозначать нормальное распределение, имеющее математическое ожиданиеи дисперсию, символом. В случае, когда,, говорят остандартном нормальном распределении. Имеются весьма подробные таблицы значений функции распределения и функции плотности стандартного нормального распределения.

Для дальнейшего нам, в первую очередь, понадобятся следующие простые свойства математического ожидания и дисперсии.

Если - некотораяпостоянная, отличная от нуля, а- некотораяслучайная величина, то тогда суммаи произведениетакже являются случайными величинами; при этом,

Два свойства, касающиеся математического ожидания, непосредственно следуют из определения математического ожидания. При выводе первого из них учитываем, что по самому определению функции плотности распределения,

Из этих двух свойств математического ожидания легко получаем указанные два свойства дисперсии. Действительно,

Таким образом, изменение случайной величины на некоторую постоянную вызывает такое же изменение математического ожидания, но не отражается на дисперсии. Изменение случайной величины в раз приводит к такому же изменению математического ожидания и изменяет значение дисперсии враз.

В применении к линейной модели наблюдений

с фиксированными и взаимно независимыми гауссовскими ошибками, мы имеем:



Соответственно,

Заметим, наконец, что если — случайные величины и, то

и если случайные величиныпопарно некоррелированы, т. е.

то тогда

В применении к последней линейной модели наблюдений это означает, что рассматриваемая как случайная величина оценка наименьших квадратов, которую мы представили ранее в виде

где

так что —фиксированные величины, имеет нормальное распределение с математическим ожиданием

и дисперсией