2.10. Проверка гипотез о значениях коэффициентов: односторонние критерии

Вспомним пример с потреблением текстиля. Мы подобрали линейную модель в логарифмах (с постоянными эластичностями)

(здесь — расходы на личное потребление текстиля,— относительная цена текстиля,- располагаемый доход). В рамках этой модели представляют интерес гипотезыио «единичной эластичности» расходов на потребление текстиля как по доходам, так и по ценам.

Построить критерии с уровнем значимости для проверки этих гипотез можно по той же схеме, по которой строятся критерии проверки гипотез, только теперь для проверки гипотезыследует использовать- статистику

а для проверки гипотезы —- статистику

Каждая из этих статистик, в случае справедливости соответствующей нулевой гипотезы, имеет распределение. Нулевая гипотеза отвергается, если значение- статистики превышает по абсолютной величине значение.

В нашем примере

Таким образом, отклонение значения от гипотетического значениястатистически значимо —гипотезаотвергается. В то же время, отклонение значенияот гипотетического значенияне является статистически значимым, игипотезане отвергается.

Замечание.Из проведенного рассмотрения видна важностьне толькоабсолютных отклоненийоценокот гипотетических значений параметров,но и точностейоценок, измеряемых дисперсиямии оцениваемых величинами. Действительно, абсолютные величины отклонений в рассмотренном примере равны

и ,

соответственно, т. е. отличаются не очень существенно. Однако примерно в 4.3 раза меньше, чем, и именно такое большое отличиеии приводит, в конечном счете,к противоположным решениямв отношении гипотези.

Итак, на основании построенной процедуры гипотеза отвергается. А что же тогда принимается?

Формально, альтернативой для в построенном критерии является гипотеза, поскольку критическое множество содержит в равной степени какбольшие положительные, так и большие (по абсолютной величине)отрицательныезначения- статистики. В то же время, значение, соответствующее отклонению, скорее говоритв пользу того, что в действительности .

В этой связи, естественным представляется более определенный выбор альтернативной гипотезы, а именно, сопоставление нулевой гипотезе односторонней альтернативы (односторонняя альтернатива — в отличие отдвухсторонней альтернативы ). При такой постановке задачи отвержение нулевой гипотезыв пользу альтернативыпроизводится толькопри больших положительных отклонениях, т. е.при больших положительных значениях -статистики. Если мы отнесем к последним значения, превышающие, то получим статистический критерий, у которого ошибка первого рода (уровень значимости) равна. Его критическое множество определяется соотношением

справа стоит теперь значение , а не, как это было при двухсторонней альтернативе. Поскольку у нас, мыотвергаемгипотезув пользу гипотезы.

Построим аналогичную процедуру для параметра . Именно, построим критерий уровнядля проверки гипотезыпротив односторонней альтернативы. Критическое множество такого критерия должно состоять из значений-статистики, превышающих. У нас значение

опять меньше порогового, так что гипотеза не отвергаетсяв пользу.

Обратим теперь внимание на то, что при рассмотрении пары конкурирующих гипотез

мы выделяем в гипотезу только одночастное значение, хотя по-существу дела проблема состоит скорее в выборе между гипотезами

Последняя ситуация коренным образом отличается от предыдущей: оказываетсясложной гипотезой, т. е. гипотезой, допускающейболее одного значения параметра, в данном случае дажебесконечно многозначений параметра. В противоположность этому, в предыдущей ситуации гипотеза былапростой.

Какие осложнения возникают при использовании сложной нулевой гипотезы?

Возьмем, для примера, частную гипотезу . Мы отвергли бы ее в пользупри

В то же время, частную гипотезу мы отвергаем в пользу той жепри

Иначе говоря, при различных частных гипотезах, входящих в состав сложной нулевой гипотезы, мы получаемразличные критические множества, обеспечивающие заданный уровень значимости (ошибку 1-го рода). Построение каждого такого множества непосредственно используетконкретное гипотетическое значение , тогда как в рамках гипотезыотдельноегипотетическое значение параметране конкретизируется.

Возникающее затруднение преодолевается, исходя из следующих соображений. Коль скоро мы не в состоянии построить единое для всехкритическое множество, вероятность попадания в которое равнапри справедливости каждой отдельной частной гипотезы, следует попытаться построить единое для всехкритическое множество, вероятность попадания в которое при выполнении каждойотдельнойчастной гипотезы была быне больше. Такая задача реализуется путем использования критического множества, соответствующего граничномузначению односторонней гипотезы, в данном случае.

Действительно, пусть мы берем критическое множество соответствующее граничной частной гипотезе, так что

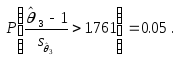
Тогда, если в действительности верна частная гипотеза то

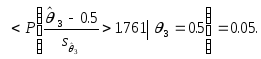
Вообще, какая бы частная гипотезани была верна, вероятность отвергнуть ее в рамках указанной процедуры не превысит.

В этом контексте,по-прежнему называетсяуровнем значимости критерия, тогда какпонятие ошибки 1-го рода уже теряет смысл для критерия в целом.Уровень значимостиограничивает сверхуошибки 1-го рода, соответствующиечастным гипотезам, входящим в состав сложной нулевой гипотезы.

Основной вывод из сказанного: при указанном подходе к построению критериев проверки сложных нулевых гипотез вида

(эластичность при

(неэластичность при

(неэластичность при

(эластичность при

против соответствующих односторонних альтернатив можно пользоваться критериями уровня , построенными для работы с теми же альтернативами, но припростых гипотезах соответственно.

Замечание.То же относится и к другим аналогичным парам гипотез, в которых вместо значения 1 берутся другие фиксированные граничные значения.