
- •Preface
- •1 A Voyage of Discovery
- •1.2 Goals
- •1.3 Organization
- •1.4 The Big Picture
- •1.5 Further Reading
- •2 The Historical Setting
- •2.2 Eras of Oceanographic Exploration
- •2.3 Milestones in the Understanding of the Ocean
- •2.4 Evolution of some Theoretical Ideas
- •2.5 The Role of Observations in Oceanography
- •2.6 Important Concepts
- •3 The Physical Setting
- •3.1 Ocean and Seas
- •3.2 Dimensions of the ocean
- •3.3 Sea-Floor Features
- •3.4 Measuring the Depth of the Ocean
- •3.5 Sea Floor Charts and Data Sets
- •3.6 Sound in the Ocean
- •3.7 Important Concepts
- •4.1 The Earth in Space
- •4.2 Atmospheric Wind Systems
- •4.3 The Planetary Boundary Layer
- •4.4 Measurement of Wind
- •4.5 Calculations of Wind
- •4.6 Wind Stress
- •4.7 Important Concepts
- •5 The Oceanic Heat Budget
- •5.1 The Oceanic Heat Budget
- •5.2 Heat-Budget Terms
- •5.3 Direct Calculation of Fluxes
- •5.4 Indirect Calculation of Fluxes: Bulk Formulas
- •5.5 Global Data Sets for Fluxes
- •5.6 Geographic Distribution of Terms
- •5.7 Meridional Heat Transport
- •5.8 Variations in Solar Constant
- •5.9 Important Concepts
- •6.2 Definition of Temperature
- •6.4 The Oceanic Mixed Layer and Thermocline
- •6.5 Density
- •6.6 Measurement of Temperature
- •6.7 Measurement of Conductivity or Salinity
- •6.8 Measurement of Pressure
- •6.10 Light in the Ocean and Absorption of Light
- •6.11 Important Concepts
- •7.1 Dominant Forces for Ocean Dynamics
- •7.2 Coordinate System
- •7.3 Types of Flow in the ocean
- •7.4 Conservation of Mass and Salt
- •7.5 The Total Derivative (D/Dt)
- •7.6 Momentum Equation
- •7.7 Conservation of Mass: The Continuity Equation
- •7.8 Solutions to the Equations of Motion
- •7.9 Important Concepts
- •8.2 Turbulence
- •8.3 Calculation of Reynolds Stress:
- •8.4 Mixing in the Ocean
- •8.5 Stability
- •8.6 Important Concepts
- •9 Response of the Upper Ocean to Winds
- •9.1 Inertial Motion
- •9.2 Ekman Layer at the Sea Surface
- •9.3 Ekman Mass Transport
- •9.4 Application of Ekman Theory
- •9.5 Langmuir Circulation
- •9.6 Important Concepts
- •10 Geostrophic Currents
- •10.1 Hydrostatic Equilibrium
- •10.2 Geostrophic Equations
- •10.3 Surface Geostrophic Currents From Altimetry
- •10.4 Geostrophic Currents From Hydrography
- •10.5 An Example Using Hydrographic Data
- •10.6 Comments on Geostrophic Currents
- •10.7 Currents From Hydrographic Sections
- •10.8 Lagrangian Measurements of Currents
- •10.9 Eulerian Measurements
- •10.10 Important Concepts
- •11.2 Western Boundary Currents
- •11.4 Observed Surface Circulation in the Atlantic
- •11.5 Important Concepts
- •12 Vorticity in the Ocean
- •12.2 Conservation of Vorticity
- •12.4 Vorticity and Ekman Pumping
- •12.5 Important Concepts
- •13.2 Importance of the Deep Circulation
- •13.3 Theory for the Deep Circulation
- •13.4 Observations of the Deep Circulation
- •13.5 Antarctic Circumpolar Current
- •13.6 Important Concepts
- •14 Equatorial Processes
- •14.1 Equatorial Processes
- •14.6 Important Concepts
- •15 Numerical Models
- •15.2 Numerical Models in Oceanography
- •15.3 Global Ocean Models
- •15.4 Coastal Models
- •15.5 Assimilation Models
- •15.6 Coupled Ocean and Atmosphere Models
- •15.7 Important Concepts
- •16 Ocean Waves
- •16.1 Linear Theory of Ocean Surface Waves
- •16.2 Nonlinear waves
- •16.3 Waves and the Concept of a Wave Spectrum
- •16.5 Wave Forecasting
- •16.6 Measurement of Waves
- •16.7 Important Concepts
- •17 Coastal Processes and Tides
- •17.1 Shoaling Waves and Coastal Processes
- •17.2 Tsunamis
- •17.3 Storm Surges
- •17.4 Theory of Ocean Tides
- •17.5 Tidal Prediction
- •17.6 Important Concepts
- •References
17.2. TSUNAMIS |
297 |
height and frequency of breaking waves and the strength of the onshore wind. Rips are a danger to unwary swimmers, especially poor swimmers bobbing along in the waves inside the breaker zone. They are carried along by the along-shore current until they are suddenly carried out to sea by the rip. Swimming against the rip is futile, but swimmers can escape by swimming parallel to the beach.
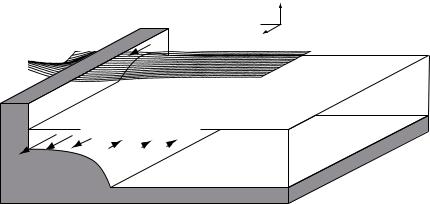
Edge waves are produced by the variability of wave energy reaching shore. Waves tend to come in groups, especially when waves come from distant storms. For several minutes breakers may be smaller than average, then a few very large waves will break. The minute-to-minute variation in the height of breakers produces low-frequency variability in the along-shore current. This, in turn, drives a low-frequency wave attached to the beach, an edge wave. The waves have periods of a few minutes, a long-shore wave length of around a kilometer, and an amplitude that decays exponentially o shore (figure 17.6).
z
x
y (north)
Figure 17.6 Computer-assisted sketch of an edge wave. Such waves exist in the breaker zone near the beach and on the continental shelf. After Cutchin and Smith (1973).
17.2Tsunamis
Tsunamis are low-frequency ocean waves generated by submarine earthquakes. The sudden motion of sea floor over distances of a hundred or more kilometers generates waves with periods of 15–40 minutes (figure 17.7). A quick calculation shows that such waves must be shallow-water waves, propagating at a speed of 180 m/s and having a wavelength of 130 km in water 3.6 km deep (figure 17.8). The waves are not noticeable at sea, but after slowing on approach to the coast, and after refraction by sub-sea features, they can come ashore and surge to heights ten or more meters above sea level. In an extreme example, the great 2004 Indian Ocean tsunami destroyed hundreds of villages, killing at least 200,000 people.
Shepard (1963, Chapter 4) summarized the influence of tsunamis based on his studies in the Pacific.
1.Tsunamis appear to be produced by movement (an earthquake) along a linear fault.
2.Tsunamis can travel thousands of kilometers and still do serious damage.

298 |
CHAPTER 17. COASTAL PROCESSES AND TIDES |
Approximate Time (hrs)
55o
50 o
45 o
40 o
35 o
30 o
25 o
20 o
|
|
|
|
KEY |
|
|
|
|
|
|
|
|
|
Orthogonals |
|
|
|
|
|
|
|
|
|
||||
Wave Fronts 2:30A.M |
|
|
|
|
|
S |
|||||||
Submarine Contours: |
|
|
|
|
D |
||||||||
|
|
1800 |
|
|
|
|
|
|
N |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
3700 |
|
|
|
|
|
A |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
5500 |
|
|
|
|
S |
L |
|
|
|
||
|
|
|
|
|
I |
|
|
|
|
||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
I |
A |
|
|
|
|
|
|
|
|
|
|
U |
T |
|
|
|
2:00AM |
|
||||
|
|
|
|
|
|
|
|
||||||
|
L |
E |
|
|
|
|
|
|
|||||
A |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2:30 |
|
|
|
|
||
|
|
|
3:00 |
|
|
|
|
|
|
|
|
||
|
4000 |
|
|
|
|
|
|
|
|
|
|
|
|
3:30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4:00 |
|
|
|
|
|
|
|
|
|
|
|
|
4:30 |
|
|
|
|
|
|
|
|
|
|
|
|
5:00 |
|
|
|
|
|
|
|
|
|
|
|
|
5:30 |
|
|
|
|
|
|
|
|
|
|
|
|
6:00 |
H |
A |
W |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||
|
|
I |
I |
|
|
|
|
|
|
|||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6:30 |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
||
7:00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-175 o |
-170 o -165 o -160 o |
||||||||||
|
|
|
|
05:00 |
|
06:00 |
|
07:00 |
|
08:00 |
|
|
|
A L A S K A |
Waimea |
|
|
|
|
|
|
|
1.0 |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
gauge |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
Height (m) |
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2700 |
20' |
||
|
|
|
3700 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1800 |
|
||
|
|
|
2700 |
|
|
|
|
|
|
6:20 |
|
|
|
|
|
1800 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
14 |
|
7.3 |
14 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
10' |
|
|
|
|
|
|
|
3.7 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
6.1 |
|
|
8.5 |
|
|
|
|
|
|
|
|
|
12m |
|
|
3.7 |
|
6:22 |
|
|
|
|
|
910 |
|
5.2 |
|
|
|
4.6 |
|
|
22 o 0 ' |
|
|
|
550 |
2.4 |
|
|
7.6 |
|
|
|||
|
|
|
|
180 |
|
WAIMEA |
|
|
2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6:24 |
|
|
N |
|
|
|
910 |
|
4.6 |
2.4 |
|
|
|
||
D |
|
|
1800 |
|
|
|
|
1800 |
|
|
||
|
|
|
|
|
|
|
|
50' |
||||
|
S |
|
|
|
|
|
|
|
|
|
2700 |
|
|
|
|
|
2700 |
|
|
|
|
|
6:26 |
|
|
|
|
|
|
6:28 |
|
|
6:28 |
|
|
|||
-155 o |
-150 o |
-160 o 0' |
50' |
|
40' |
30' |
20' |
|
10' |
|
||
Figure 17.7 Left Hourly positions of leading edge of tsunami generated by the large earthquake in the Aleutian Trench on April 1, 1946 at 1:59 AM Hawaiian time (12:59 GMT). Right: top Sealevel recorded by a river gauge in the estuary of the Waimea River. Right: lower Map of Kauai showing the heights reached by the water (in meters above lower low water) during the tsunami, wave fronts, orthogonals, and submarine contours. Times refer to the computed arrival time of the first wave. After Shepard, MacDonald, and Cox (1950).
3.The first wave of a tsunami is not likely to be the biggest.
4.Wave amplitudes are relatively large shoreward of submarine ridges. They are relatively low shoreward of submarine valleys, provided the features extend into deep water.
5.Wave amplitudes are decreased by the presence of coral reefs bordering the coast.
6.Some bays have a funneling e ect, but long estuaries attenuate waves.
7.Waves can bend around circular islands without great loss of energy, but they are considerably smaller on the backsides of elongated, angular islands.
Numerical models are used to forecast tsunami heights throughout ocean basins and the inundation of coasts. For example, noaa’s Center for Tsunami Research uses the Method of Splitting Tsunami most model (Titov and Gonzalez, 1997). The model uses nested grids to resolve the tsunami wavelength, it

17.3. STORM SURGES |
299 |
|
|
|
|
|
|
|
Figure 17.8 Tsunami waves four hours after the great M9 Cascadia earthquake o the coast of Washington on 26 January 1700 calculated by a finite-element, numerical model. Maximum open-ocean wave height, about one meter, is north of Hawaii. After Satake et al. (1996).
propagates the wave across ocean basins, and then calculates run-up when the wave comes ashore. It is initialized from a ground deformation model that uses measured earthquake magnitude and location to calculate vertical displacement of the sea floor. The forcing is modified once waves are measured near the earthquake by seafloor observing stations.
17.3Storm Surges
Storm winds blowing over shallow, continental shelves pile water against the coast. The increase in sea level is known as a storm surge. Several processes are important:
1.Ekman transport by winds parallel to the coast transports water toward the coast causing a rise in sea level.
2.Winds blowing toward the coast push water directly toward the coast.
3.Wave run-up and other wave interactions transport water toward the coast adding to the first two processes.
4.Edge waves generated by the wind travel along the coast.
5.The low pressure inside the storm raises sea level by one centimeter for each millibar decrease in pressure through the inverted-barometer e ect.
6.Finally, the storm surge adds to the tides, and high tides can change a relative weak surge into a much more dangerous one.
See Graber et al (2006) and §15.5 for a description of Advanced Circulation Model used by the National Hurricane Center for predicting storm-surges.
To a crude first approximation, wind blowing over shallow water causes a slope in the sea surface proportional to wind stress.
∂ζ |
= |
τ0 |
(17.4) |
|
∂x |
ρgH |
|||
|
|
300 |
CHAPTER 17. COASTAL PROCESSES AND TIDES |
Storm Surge (m)
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1894 |
|
|
1953 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1904 |
1916 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1906 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1928 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mean High Water |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 3 |
|
10 2 |
10 |
1 |
10 - 1 |
10 - 2 |
10 - 3 |
10 - 4 |
||||||||||||
Frequency per year
Figure 17.9 Probability (per year) density distribution of vertical height of storm surges in the Hook of Holland in the Netherlands. The distribution function is Rayleigh, and the probability of large surges is estimated by extrapolating the observed frequency of smaller, more common surges. After Wiegel (1964: 113).
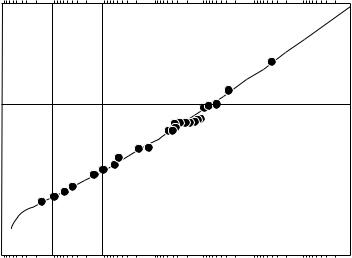
where ζ is sea level, x is horizontal distance, H is water depth, T0 is wind stress at the sea surface, ρ is water density; and g is gravitational acceleration.
If x = 100 km, U = 40 m/s, and H = 20 m, values typical of a hurricane o shore of the Texas Gulf Coast, then T = 2.7 Pa, and ζ = 1.3 m at the shore. Figure 17.9 shows the frequency of surges at the Netherlands and a graphical method for estimating the probability of extreme events using the probability of weaker events.
17.4Theory of Ocean Tides
Tides have been so important for commerce and science for so many thousands of years that tides have entered our everyday language: time and tide wait for no one, the ebb and flow of events, a high-water mark, and turn the tide of battle.
1.Tides produce strong currents in many parts of the ocean. Tidal currents can have speeds of up to 5 m/s in coastal waters, impeding navigation and mixing coastal waters.
2.Tidal currents generate internal waves over seamounts, continental slopes, and mid-ocean ridges. The waves dissipate tidal energy. Breaking internal waves and tidal currents are a major force driving oceanic mixing.
3.Tidal mixing helps drive the deep circulation, and it influences climate and abrupt climate change.
4.Tidal currents can suspend bottom sediments, even in the deep ocean.
17.4. THEORY OF OCEAN TIDES |
301 |
5.Earth’s crust is elastic. It bends under the influence of the tidal potential. It also bends under the weight of oceanic tides. As a result, the sea floor, and the continents move up and down by about 10 cm in response to the tides. The deformation of the solid earth influence almost all precise geodetic measurements.
6.Oceanic tides lag behind the tide-generating potential. This produces forces that transfer angular momentum between earth and the tide producing body, especially the moon. As a result of tidal forces, earth’s rotation about it’s axis slows, increasing the length of day; the rotation of the moon about earth slows, causing the moon to move slowly away from earth; and moon’s rotation about it’s axis slows, causing the moon to keep the same side facing earth as the moon rotates about earth.
7.Tides influence the orbits of satellites. Accurate knowledge of tides is needed for computing the orbit of altimetric satellites and for correcting altimeter measurements of oceanic topography.
8.Tidal forces on other planets and stars are important for understanding many aspects of solar-system dynamics and even galactic dynamics. For example, the rotation rate of Mercury, Venus, and Io result from tidal forces.
Mariners have known for at least four thousand years that tides are related to the phase of the moon. The exact relationship, however, is hidden behind many complicating factors, and some of the greatest scientific minds of the last four centuries worked to understand, calculate, and predict tides. Galileo, Descartes, Kepler, Newton, Euler, Bernoulli, Kant, Laplace, Airy, Lord Kelvin, Je reys, Munk and many others contributed. Some of the first computers were developed to compute and predict tides. Ferrel built a tide-predicting machine in 1880 that was used by the U.S. Coast Survey to predict nineteen tidal constituents. In 1901, Harris extended the capacity to 37 constituents.
Despite all this work important questions remained: What is the amplitude and phase of the tides at any place on the ocean or along the coast? What is the speed and direction of tidal currents? What is the shape of the tides on the ocean? Where is tidal energy dissipated? Finding answers to these simple questions is di cult, and the first, accurate, global maps of deep-sea tides were only published in 1994 (LeProvost et al. 1994). The problem is hard because the tides are a self-gravitating, near-resonant, sloshing of water in a rotating, elastic, ocean basin with ridges, mountains, and submarine basins.
Predicting tides along coasts and at ports is much easier. Data from a tide gauge plus the theory of tidal forcing gives an accurate description of tides near the tide gauge.
Tidal Potential Tides are calculated from the hydrodynamic equations for a self-gravitating ocean on a rotating, elastic earth. The driving force is the gradient of the gravity field of the moon and sun. If the earth were an ocean planet with no land, and if we ignore the influence of inertia and currents, the gravity gradient produces a pair of bulges of water on earth, one on the side

302 |
CHAPTER 17. COASTAL PROCESSES AND TIDES |
facing the moon or sun, one on the side away from the moon or sun. A clear derivation of the forces is given by Pugh (1987) and by Dietrich, Kalle, Krauss, and Siedler (1980). Here I follow the discussion in Pugh (1987: §3.2).
Note that many oceanographic books state that the tide is produced by two processes: i) the centripetal acceleration at earth’s surface as the earth and moon circle around a common center of mass, and ii) the gravitational attraction of mass on earth and the moon. However, the derivation of the tidal potential does not involve centripetal acceleration, and the concept is not used by the astronomical or geodetic communities.
Earth |
P |
|
r1 |
Celestial |
|
r |
|
|
ϕ |
|
body |
O |
|
|
|
R |
A |
|
|
Figure 17.10 Sketch of coordinates for determining the tide-generating potential.
To calculate the amplitude and phase of the tide on an ocean planet, we begin by calculating the tide-generating potential. This is much easier than calculating the forces. Ignoring for now earth’s rotation, the rotation of moon about earth produces a potential VM at any point on earth’s surface
γM |
(17.5) |
VM = − r1 |
where the geometry is sketched in figure 17.10, γ is the gravitational constant, and M is moon’s mass. From the triangle OP A in the figure,
r12 = r2 + R2 − 2rR cos ϕ |
(17.6) |
Using this in (17.5) gives
VM = − R |
1 − 2 |
R cos ϕ + |
R |
|
(17.7) |
|||
|
γM |
|
|
r |
|
r |
2 |
−1/2 |
r/R ≈ 1/60, and (17.7) may be expanded in powers of r/R using Legendre polynomials (Whittaker and Watson, 1963: §15.1):
VM = − R |
1 + |
R cos ϕ + |
R |
|
2 |
|
2 |
|
(3 cos2 |
ϕ − 1) + · · · |
(17.8) |
|||
|
γM |
|
|
r |
|
r |
|
|
1 |
|
|
|
|
|
The tidal forces are calculated from the spatial gradient of the potential. The first term in (17.8) produces no force. The second term, when di erentiated with respect to (r cos ϕ) produces a constant force γM/R2 parallel to OA that keeps earth in orbit around the center of mass of the earth-moon system. The third term produces the tides, assuming the higher-order terms can be ignored. The tide-generating potential is therefore:
V = − |
γM r2 |
|
2R3 (3 cos2 ϕ − 1) |
(17.9) |
17.4. THEORY OF OCEAN TIDES |
303 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 o
30 o
Z
0 o
 -30 o
-30 o
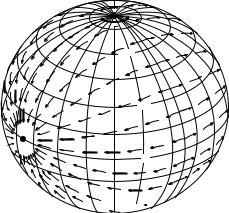
Figure 17.11 The horizontal component of the tidal force on earth when the tide-generating body is above the Equator at Z. After Dietrich et al. (1980: 413).
The tide-generating force can be decomposed into components perpendicular P and parallel H to the sea surface. Tides are produced by the horizontal component. “The vertical component is balanced by pressure on the sea bed, but the ratio of the horizontal force per unit mass to vertical gravity has to be balanced by an opposing slope of the sea surface, as well as by possible changes in current momentum” (Cartwright, 1999: 39, 45). The horizontal component, shown in figure 17.11, is:
H = − |
1 ∂V |
= |
2G |
sin 2ϕ |
(17.10) |
||||||
|
|
|
|
|
|
|
|
||||
r |
|
∂ϕ |
|
r |
|||||||
where |
|
|
|
|
|
|
|||||
3 |
γM |
r2 |
(17.11) |
||||||||
G = |
|
|
|||||||||
4 |
R3 |
||||||||||
The tidal potential is symmetric about the earth-moon line, and it produces symmetric bulges.
If we allow our ocean-covered earth to rotate, an observer in space sees the two bulges fixed relative to the earth-moon line as earth rotates. To an observer on earth, the two tidal bulges seems to rotate around earth because moon appears to move around the sky at nearly one cycle per day. Moon produces high tides every 12 hours and 25.23 minutes on the equator if the moon is above the equator. Notice that high tides are not exactly twice per day because the moon is also rotating around earth. Of course, the moon is above the equator only twice per lunar month, and this complicates our simple picture of the tides on an ideal ocean-covered earth. Furthermore, moon’s distance from earth R varies because moon’s orbit is elliptical and because the elliptical orbit is not fixed.
Clearly, the calculation of tides is getting more complicated than we might have thought. Before continuing on, we note that the solar tidal forces are derived in a similar way. The relative importance of the sun and moon are
304 |
CHAPTER 17. COASTAL PROCESSES AND TIDES |
nearly the same. Although the sun is much more massive than moon, it is much further away.
Gsun = GS = |
3 |
γS |
|
r2 |
|
|
(17.12) |
|||
4 |
Rsun3 |
|
|
|||||||
Gmoon = GM = |
3 |
γM |
r2 |
|
|
(17.13) |
||||
4 |
Rmoon3 |
|||||||||
|
GS |
= 0.46051 |
|
|
(17.14) |
|||||
|
|
|
|
|||||||
|
GM |
|
|
|
|
|
|
|
|
|
where Rsun is the distance to the sun, S is the mass of the sun, Rmoon is the distance to the moon, and M is the mass of the moon.
Coordinates of Sun and Moon Before we can proceed further we need to know the position of moon and sun relative to earth. An accurate description of the positions in three dimensions is very di cult, and it involves learning arcane terms and concepts from celestial mechanics. Here, I paraphrase a simplified description from Pugh (1987). See also figure 4.1.
A natural reference system for an observer on earth is the equatorial system described at the start of Chapter 3. In this system, declinations δ of a celestial body are measured north and south of a plane which cuts the earth’s equator.
Angular distances around the plane are measured relative to a point on this celestial equator which is fixed with respect to the stars. The point chosen for this system is the vernal equinox, also called the ‘First Point of Aries’. . . The angle measured eastward, between Aries and the equatorial intersection of the meridian through a celestial object is called the right ascension of the object. The declination and the right ascension together define the position of the object on a celestial background. . .
[Another natural reference] system uses the plane of the earth’s revolution around the sun as a reference. The celestial extension of this plane, which is traced by the sun’s annual apparent movement, is called the ecliptic. Conveniently, the point on this plane which is chosen for a zero reference is also the vernal equinox, at which the sun crosses the equatorial plane from south to north around 21 March each year. Celestial objects are located by their ecliptic latitude and ecliptic longitude. The angle between the two planes, of 23.45◦, is called the obliquity of the ecliptic. . . —Pugh (1987: 72).
Tidal Frequencies Now, let’s allow earth to spin about its polar axis. The changing potential at a fixed geographic coordinate on earth is:
cos ϕ = sin ϕp sin δ + cos ϕp cos δ cos(τ1 − 180◦) |
(17.15) |
where ϕp is latitude at which the tidal potential is calculated, δ is declination of moon or sun north of the equator, and τ1 is the hour angle of moon or sun. The hour angle is the longitude where the imaginary plane containing the sun or moon and earth’s rotation axis crosses the Equator.

17.4. THEORY OF OCEAN TIDES |
305 |
The period of the solar hour angle is a solar day of 24 hr 0 m. The period of the lunar hour angle is a lunar day of 24 hr 50.47 m.
Earth’s axis of rotation is inclined 23.45◦ with respect to the plane of earth’s orbit about the sun. This defines the ecliptic, and the sun’s declination varies between δ = ±23.45◦ with a period of one solar year. The orientation of earth’s rotation axis precesses with respect to the stars with a period of 26 000 years. The rotation of the ecliptic plane causes δ and the vernal equinox to change slowly, and the movement called the precession of the equinoxes.
Earth’s orbit about the sun is elliptical, with the sun in one focus. That point in the orbit where the distance between the sun and earth is a minimum is called perigee. The orientation of the ellipse in the ecliptic plane changes slowly with time, causing perigee to rotate with a period of 20 942 years. Therefore Rsun varies with this period.
Moon’s orbit is also elliptical, but a description of moon’s orbit is much more complicated than a description of earth’s orbit. Here are the basics. The moon’s orbit lies in a plane inclined at a mean angle of 5.15◦ relative to the plane of the ecliptic. And lunar declination varies between δ = 23.45 ± 5.15◦ with a period of one tropical month of 27.32 solar days. The actual inclination of moon’s orbit varies between 4.97◦, and 5.32◦.
The shape of moon’s orbit also varies. First, perigee rotates with a period of 8.85 years. The eccentricity of the orbit has a mean value of 0.0549, and it varies between 0.044 and 0.067. Second, the plane of moon’s orbit rotates around earth’s axis of rotation with a period of 18.613 years. Both processes cause variations in Rmoon.
Note that I am a little imprecise in defining the position of the sun and moon. Lang (1980: § 5.1.2) gives much more precise definitions.
Substituting (17.15) into (17.9) gives:
V = γM3r2 1 3 sin2 ϕp − 1 3 sin2 δ − 1
R 4
+ 3 sin 2ϕp sin 2δ cos τ1
+ 3 cos2 ϕp cos2 δ cos 2τ1 (17.16)
Equation (17.16) separates the period of the lunar tidal potential into three terms with periods near 14 days, 24 hours, and 12 hours. Similarly the solar potential has periods near 180 days, 24 hours, and 12 hours. Thus there are three distinct groups of tidal frequencies: twice-daily, daily, and long period, having di erent latitudinal factors sin2 θ, sin 2θ, and (1 − 3 cos2 θ)/2, where θ is the co-latitude (90◦ − ϕ).
Doodson (1922) expanded (17.16) in a Fourier series using the cleverly chosen frequencies in table 17.1. Other choices of fundamental frequencies are possible, for example the local, mean, solar time can be used instead of the local, mean, lunar time. Doodson’s expansion, however, leads to an elegant decomposition of tidal constituents into groups with similar frequencies and spatial variability.
Using Doodson’s expansion, each constituent of the tide has a frequency
f = n1f1 + n2f2 + n3f3 + n4f4 + n5f5 + n6f6 |
(17.17) |

306 |
|
CHAPTER 17. COASTAL PROCESSES AND TIDES |
||
Table 17.1 Fundamental Tidal Frequencies |
||||
|
|
|
|
|
|
Frequency |
|
Period |
Source |
|
◦/hour |
|
|
|
|
|
|
|
|
f1 |
14.49205211 |
1 |
lunar day |
Local mean lunar time |
f2 |
0.54901653 |
1 |
month |
Moon’s mean longitude |
f3 |
0.04106864 |
1 |
year |
Sun’s mean longitude |
f4 |
0.00464184 |
8.847 |
years |
Longitude of moon’s perigee |
f5 |
-0.00220641 |
18.613 |
years |
Longitude of moon’s ascending node |
f6 |
0.00000196 |
20,940 |
years |
Longitude of sun’s perigee |
|
|
|
|
|
where the integers ni are the Doodson numbers. n1 = 1, 2, 3 and n2–n6 are between −5 and +5. To avoid negative numbers, Doodson added five to n2···6. Each tidal wave having a particular frequency given by its Doodson number is called a tidal constituent , sometimes called a partial tides. For example, the principal, twice-per-day, lunar tide has the number 255.555. Because the very long-term modulation of the tides by the change in sun’s perigee is so small, the last Doodson number n6 is usually ignored.
If the ocean surface is in equilibrium with the tidal potential, which means we ignore inertia and currents and assume no land (Cartwright 1999: 274), the largest tidal constituents would have amplitudes given in table 17.2. Notice that tides with frequencies near one or two cycles per day are split into closely spaced lines with spacing separated by a cycle per month. Each of these lines is further split into lines separated by a cycle per year (figure 17.12). Furthermore, each of these lines is split into lines separated by a cycle per 8.8 yr, and so on.
Table 17.2 Principal Tidal Constituents
|
|
|
|
|
|
|
Equilibrium |
|
Tidal |
|
|
|
|
|
|
Amplitude† |
Period |
Species |
Name |
n1 |
n2 |
n3 |
n4 |
n5 |
(m) |
(hr) |
|
|
|
|
|
|
|
|
|
Semidiurnal |
n1 = 2 |
|
|
|
|
|
|
|
Principal lunar |
M2 |
2 |
0 |
0 |
0 |
0 |
0.242334 |
12.4206 |
Principal solar |
S2 |
2 |
2 |
-2 |
0 |
0 |
0.112841 |
12.0000 |
Lunar elliptic |
N2 |
2 |
-1 |
0 |
1 |
0 |
0.046398 |
12.6584 |
Lunisolar |
K2 |
2 |
2 |
0 |
0 |
0 |
0.030704 |
11.9673 |
|
|
|
|
|
|
|
|
|
Diurnal |
n1 = 1 |
|
|
|
|
|
|
|
Lunisolar |
K1 |
1 |
1 |
0 |
0 |
0 |
0.141565 |
23.9344 |
Principal lunar |
O1 |
1 |
-1 |
0 |
0 |
0 |
0.100514 |
25.8194 |
Principal solar |
P1 |
1 |
1 |
-2 |
0 |
0 |
0.046843 |
24.0659 |
Elliptic lunar |
Q1 |
1 |
-2 |
0 |
1 |
0 |
0.019256 |
26.8684 |
|
|
|
|
|
|
|
|
|
Long Period |
n1 = 0 |
|
|
|
|
|
|
|
Fortnightly |
M f |
0 |
2 |
0 |
0 |
0 |
0.041742 |
327.85 |
Monthly |
M m |
0 |
1 |
0 |
-1 |
0 |
0.022026 |
661.31 |
Semiannual |
Ssa |
0 |
0 |
2 |
0 |
0 |
0.019446 |
4383.05 |
|
|
|
|
|
|
|
|
|
†Amplitudes from Apel (1987)
17.4. THEORY OF OCEAN TIDES |
307 |
Amplitude (cm)
Amplitude (cm)
10 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2N |
2 |
|
µ |
|
|
|
ν2 |
|
|
|
|
|
|
L2 T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
3N |
|
ε2 |
|
|
|
|
|
|
|
|
α |
|
|
|
λ2 |
|
|
|
|
|
|
|
|
|
R2 |
|
|
η2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
β |
2 |
|
|
|
|
|
|
|
|
|
ζ2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
10 - 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ2 |
|
|
|
|
|
|
|
2T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
10 - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
26 |
|
27 |
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
29 |
|
30 |
|
|
|
|
|
|
|
|
31 |
|
|
|
32 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Frequency (deg/hr) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
10 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
10 - 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10 - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
29.80 |
29.85 |
|
|
|
29.90 |
|
|
29.95 |
|
|
|
30.00 |
30.05 |
|
|
|
|
|
|
30.10 |
30.15 |
30.20 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Frequency (deg/hr) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
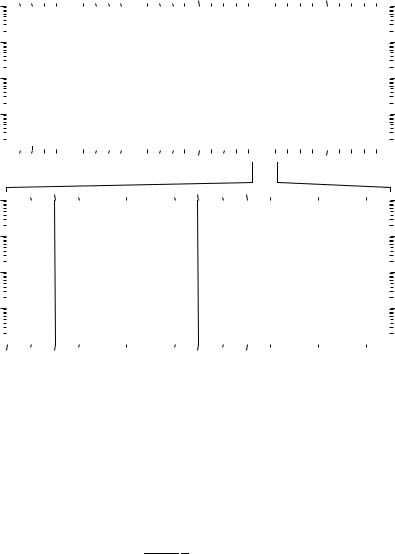
Figure 17.12 Upper: Spectrum of equilibrium tides with frequencies near twice per day. The spectrum is split into groups separated by a cycle per month (0.55 deg/hr). Lower: Expanded spectrum of the S2 group, showing splitting at a cycle per year (0.04 deg/hr). The finest splitting in this figure is at a cycle per 8.847 years (0.0046 deg/hr). From Richard Eanes, Center for Space Research, University of Texas.
Clearly, there are very many possible tidal constituents.
Why is the tide split into the many constituents shown in figure 17.12? To answer the question, suppose moon’s elliptical orbit was in the equatorial plane of earth. Then δ = 0. From (17.16), the tidal potential on the equator, where ϕp = 0, is:
|
γM r2 1 |
|
V = |
R3 4 cos (4πf1) |
(17.18) |
If the ellipticity of the orbit is small, R = R0(1+ǫ), and (17.18) is approximately
V = a(1 − 3ǫ) cos (4πf1) |
(17.19) |
where a = γM r2 / 4R3 is a constant. and we can write ǫ = b cos(2πf2) where simplifications, (17.19) can be written:
ǫ varies with a period of 27.32 days, b is a small constant. With these
V |
= a cos (4πf1) − 3ab cos (2πf2) cos (4πf1) |
(17.20a) |
V |
= a cos (4πf1) − 3ab [cos 2π (2f1 − f2) + cos 2π (2f1 + f2)] |
(17.20b) |
