5.3. Мгновенный центр скоростей. Центроиды

Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

Докажем теорему о существовании мгновенного центра скоростей: если угловая скорость плоской фигуры отлична от нуля, то мгновенный центр скоростей существует.

Пусть скорость произвольной точки плоской фигуры отлична от нуля (в противном случае точка А была бы мгновенным центром скоростей).

Рис. 5.6.

По знаку угловой скорости определяем направление вращения плоской фигуры вокруг точки А и в этом направлении откладываем от точки А отрезок перпендикулярно скорости (рис. 5.6). В соответствии с формулой (5.5) имеем

.

Так как скорость перпендикулярна АР, то вектор параллелен . Кроме того, в соответствии с правилом построения отрезка АР векторы и имеют противоположные направления. Модуль скорости равен

.

Два вектора, равных по величине и противоположно направленных, в сумме равны нулю. Следовательно,

,

т.е. скорость точки Р равна нулю.

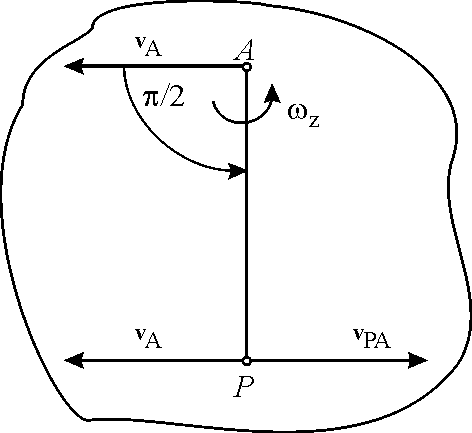
Рис. 5.7.

Выберем теперь за полюс точку Р. Тогда скорость произвольной точки А плоской фигуры найдется по формуле (рис. 5.7) , (5.6) т.к. . Отсюда следует, что скорости точек тела при его плоском движении распределяются точно так же,

как и при вращательном движении. Роль неподвижной оси играет мгновенная ось, проходящая через мгновенный центр скоростей перпендикулярно плоскости движения. Таким образом, скорости всех точек фигуры перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром скоростей , а модули скоростей пропорциональны расстояниям до мгновенного центра скоростей .

Зная положение мгновенного центра скоростей, можно найти скорости всех точек плоской фигуры, если известна скорость какой-либо ее точки.

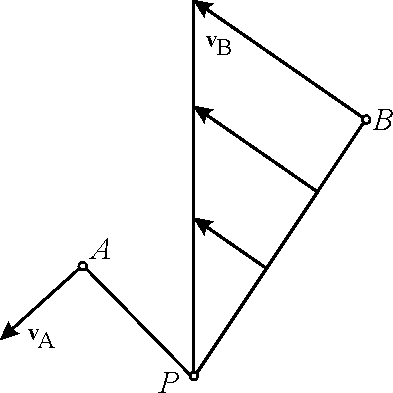
В самом деле, пусть известна, например, скорость точки А; тогда из равенства найдем и скорость любой точки В будет . Соединив конец вектора с точкой Р, получим эпюру распределения скоростей вдоль отрезка РВ (см. рис. 5.7).

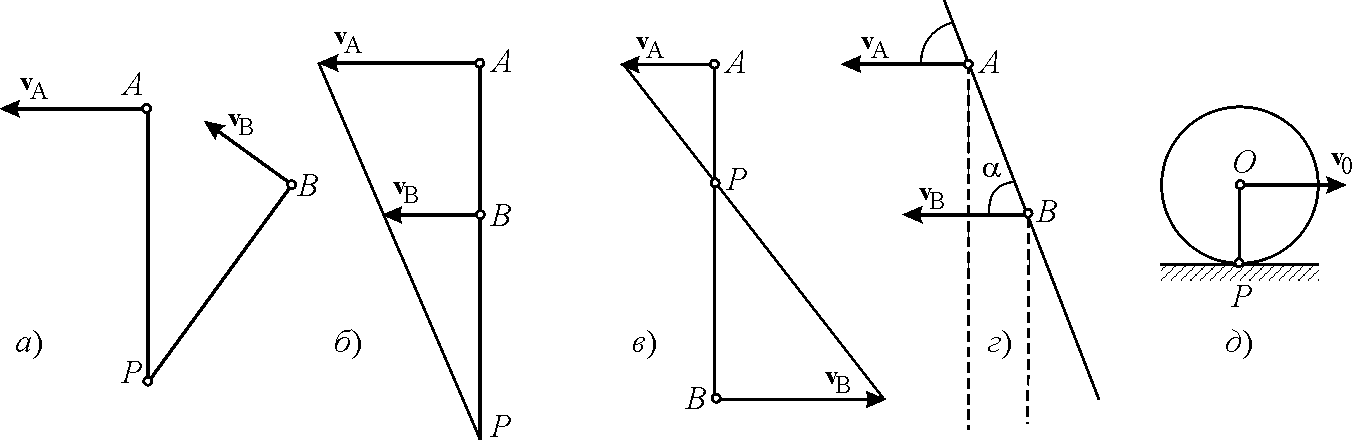
Используя основные свойства мгновенного центра скоростей, можно определить его положение и в других случаях. На рис. 5.8 а показано, как находится эта точка, когда известны направления скоростей двух точек. Из точек А и В восставлены перпендикуляры к и . Точка Р находится на их пересечении. Если скорости точек А и В параллельны и , то для определения мгновенного центра скоростей следует воспользоваться свойством пропорциональности модулей скоростей расстояниям точек до мгновенного центра скоростей. На рис. 5.8 б и в показано, как находится мгновенный центр в этих случаях.

Рис. 5.8.

На рис. 5.8 г показан случай, когда и параллельны, но не перпендикулярна отрезку АВ. Очевидно, что в этом случае прямые; перпендикулярные и , пересекаются в бесконечности и мгновенного центра скоростей не существует. В самом деле, на основании теоремы о проекциях скоростей имеем . Отсюда и . Из формулы (5.5) следует, что при этом , т.е. угловая скорость фигуры равна нулю . Значит, в данный момент времени скорости всех точек плоской фигуры равны по модулю и направлению и, следовательно, точки, линейная скорость которой равна нулю, не существует.

При качении без скольжения одного тела по поверхности другого (рис. 5.8 д) мгновенный центр скоростей совпадает с точкой соприкосновения тел (так как при отсутствии скольжения скорость точки соприкосновения равна нулю).

Использование мгновенного центра скоростей очень часто упрощает решение задачи.

В отличие от чисто вращательного движения, при плоском движении мгновенный центр скоростей меняет, вообще говоря, свое положение на плоскости. Если наклеить на фигуру, совершающую плоское движение, лист бумаги и в каждый момент времени прокалывать иглой мгновенный центр скоростей, то получатся две серии отметок: одна на неподвижной плоскости, другая на листе, связанном с фигурой.

Геометрическое место мгновенных центров скоростей, отмеченных на неподвижной плоскости, называется неподвижной центроидой.

Геометрическое место мгновенных центров скоростей, отмеченных на плоскости, жестко связанной фигурой, называется подвижной центроидой.

При качении цилиндра по горизонтальной плоскости (рис. 5.8 д) неподвижная центроида – горизонтальная прямая, а подвижная – окружность.

В каждый момент времени подвижная и неподвижная центроиды имеют общую точку касания – мгновенный центр скоростей Р, т.е. точку, скорость которой равна нулю. Поэтому плоское движение можно представить, как качение без скольжения подвижной центроиды по неподвижной.