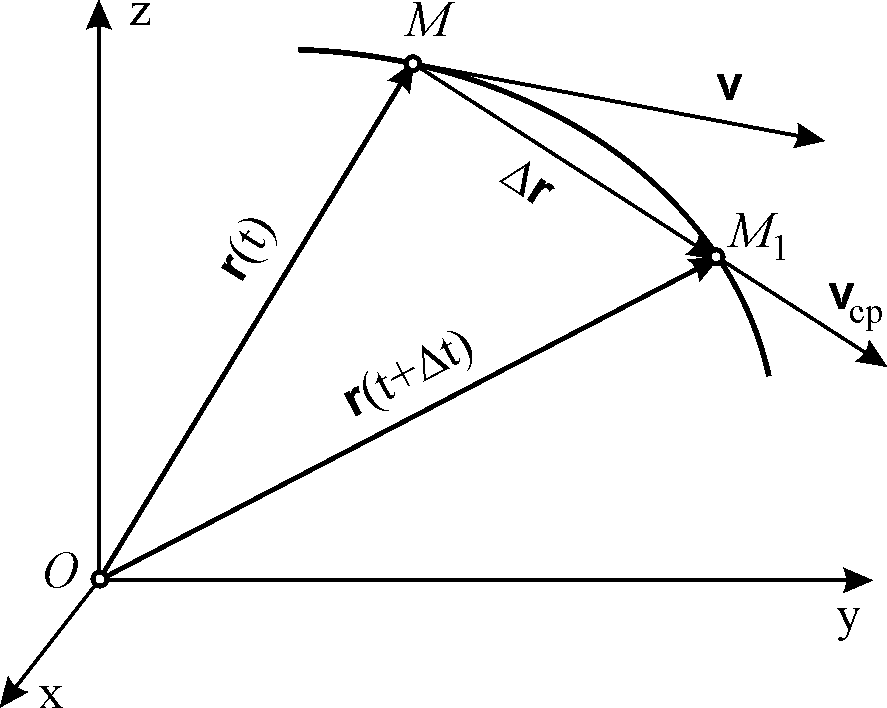
3.2. Скорость точки

Пусть в момент времени положение точки определяется радиусом-вектором , а в момент радиусом-вектором . Вектор

будем называть вектором перемещения точки за время (рис. 3.7).

Рис. 3.7.

Отношение вектора к промежутку времени М называется средней скоростью точки за промежуток времени . Скоростью в данный момент времени называется предел отношения вектора

перемещения точки к промежутку времени, за который произошло это перемещение, когда этот промежуток времени стремится к нулю, т.е.

. (3.9)

Из этого определения видно, что скорость точки равна производной радиуса-вектора точки по времени. На рис. 3.7 показаны средняя скорость и скорость точки М. Как следует из общей теории, скорость точки  – этор вектор, направленный по касательной к траектории в сторону движения точки.

3.2.1. Скорость точки при координатном способе задания движения Декартова система координат

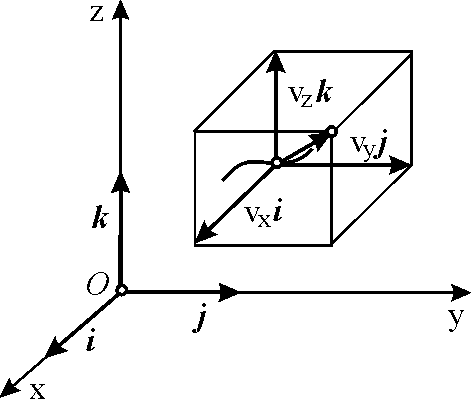
Пусть движение точки задано в декартовой системе координат, принятой за неподвижную, т.е. пусть заданы координаты точки как функции времени

, , .

Согласно выражению (3.6) имеем .

Так как единичные векторы выбранной системы координат постоянны, то на основании формулы (3.9) получаем

.

Рис. 3.8.

На рис. 3.8 показано разложение скорости на составляющие по осям координатной системы Oxyz. Таким образом, проекции скорости , , на координатные оси будут , , .

т.е. проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.

Модуль скорости определяется формулой

, (3.10)

а направление скорости – направляющими косинусами

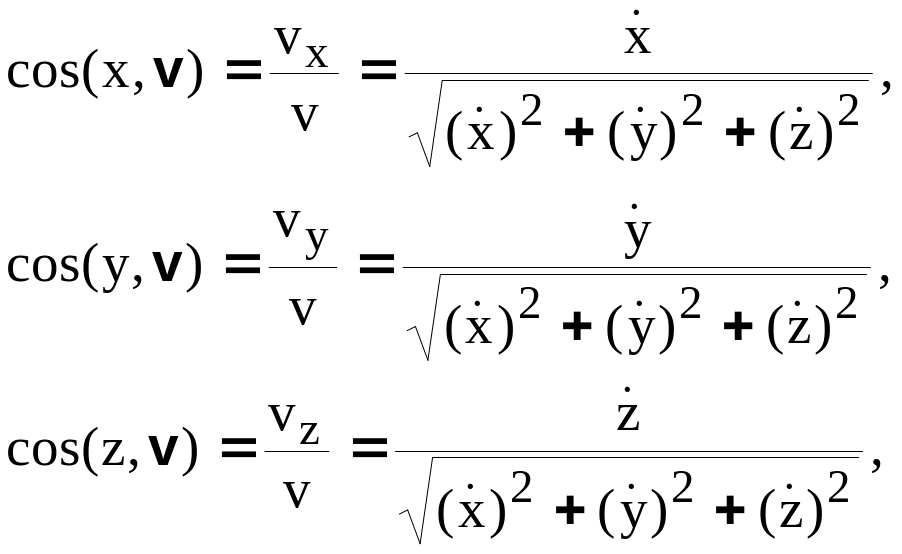(3.11)

Если модуль скорости не изменяется с течением времени, то движение называется равномерным.

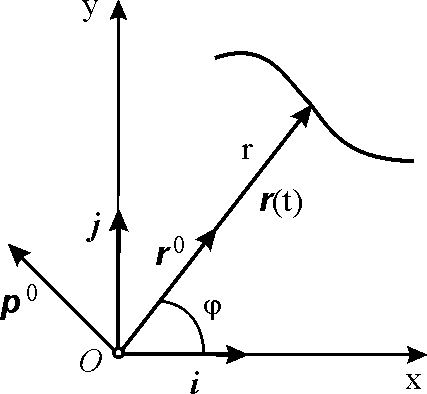
Полярные координаты

Введем в рассмотрение единичные векторы: , направленный по радиусу-вектору в сторону возрастания , и , повернутый относительно на угол в сторону возрастания угла (рис. 3.9). Единичные векторы и могут быть представлены через единичные векторы координатных осей:

,

.

Рис.3.9.

Рис. 3.10.

Производные по времени от единичных векторов , определяются соотношениями

, (3.12)

. (3.13)

Радиус-вектор , определяющий положение точки, может быть представлен в виде (рис. 3.9). При движении точки меняются как модуль, так и направление радиуса-вектора , следовательно, и , и являются функциями времени. На основании равенства (3.9) имеем

.

Используя соотношение (3.12), будем иметь

.

Полученная формула дает разложение вектора скорости на две взаимно перпендикулярные составляющие: радиальную и поперечную (рис. 3.10).

Проекции скорости на радиальное и поперечное направления

и (3.14)

называются соответственно радиальной и поперечной скоростями. Модуль скорости находится по формуле

. (3.15)

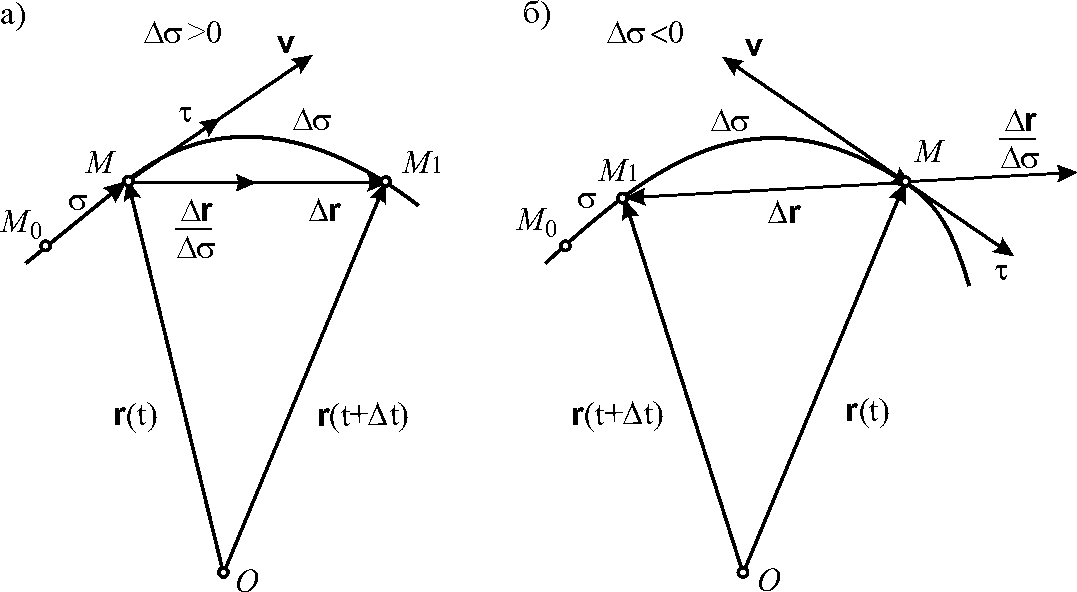
3.2.2. Скорость точки при естественном способе задания движения. Пусть точка М движется по какой-либо кривой (рис. 3.11). За промежуток времени точка переместится по кривой из положения М в положение М₁. Дуга , если движение точки происходит в сторону положительного отсчета дуги (рис. 3.11 а), и , если движение происходит в противоположную сторону (рис. 3.11 б). На основании (3.9) имеем .

Перепишем это равенство в виде

.

Так как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секущей ММ₁ совпадает с направлением касательной к кривой в точке М, то

,

где  – единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.

Рис. 3.11.

Действительно, если , то вектор направлен в сторону (см. рис. 3.11 а), а при вектор направлен в сторону, противоположную (см. рис. 3.11 б). В обоих случаях этот вектор, а следовательно, и его предел , направлены в сторону возрастания дуги (на рис. 3.11 положительное направление отсчета дуги выбрано вправо от начала отсчета М₀).

Учитывая, что ,

имеем . (3.16)

Обозначая , получим

. (3.17)

Из формулы (3.17) следует, что . Очевидно, что , если движение происходит в сторону положительного отсчета дуги, и , если движение происходит в противоположную сторону.

Так как проходимый точкой путь всегда положителен, то элемент пути

и, следовательно, модуль скорости можно определить по формуле

.