2.4. Основные правила дифференцирования вектор-функций.

1. Если  – постоянный вектор, то .

2.  Производная суммы вектор-функций равна сумме производных слагаемых

.

3. Пусть вектор-функция умножается на скалярную функцию того же скалярного аргумента. Тогда

.

4. Производные скалярного и векторного произведения вектор-функций соответственно определяются выражениями:

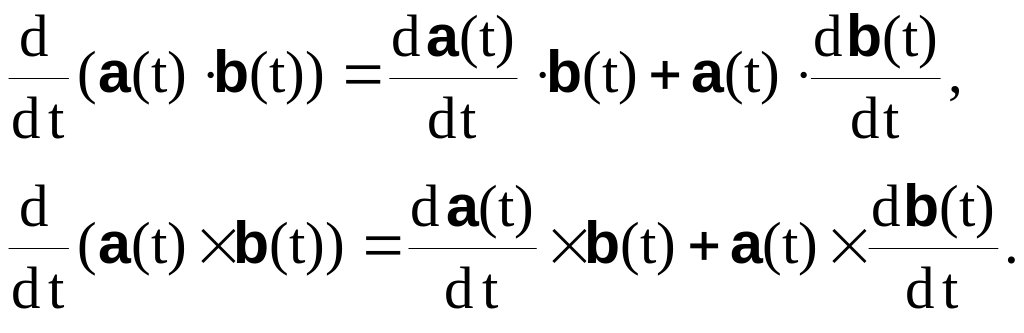
Пусть вектор-функция задана в неподвижной прямоугольной системе координат; тогда

,

где  – проекции вектор-функции на оси (рис. 2.2). Так как векторы постоянные, то

.

С другой стороны, вектор можно записать через его проекции следующим образом:

.

Сравнивая оба выражения, найдем проекции производной вектора на координатные оси

, , .

Следовательно, проекции производной вектора на неподвижные оси равны производным от соответствующих проекций вектора.

Модуль производной определяется из равенства

.

Если модуль вектор-функции остается постоянным при изменении аргумента , то годографом вектор-функции будет кривая, расположенная на сфере радиуса а. Следовательно, производная , направленная по касательной к годографу вектор-функции , будет в этом случае перпендикулярна вектору .

2.5. Интегрирование вектор-функции скалярного аргумента.

Вектор-функция называется первообразной функцией для вектор-функции при , если дифференцируема и

, .

Неопределенным интегралом от вектор-функции скалярного аргумента называется совокупность всех первообразных для

,

где  – какая-нибудь из первообразных для ;

 – произвольный постоянный вектор.

Для интегралов от вектор-функций справедливы следующие свойства

1.  , .

2.  .

3. Кинематика точки

3.1. Способы задания движения

Движение точки по отношению к избранной системе отсчета считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени. Существуют три способа задания движения точки: векторный, координатный и естественный.

3.1.1. Векторный способ. Положение точки М, движущейся по отношению к системе отсчета Oxyz, можно определить, задав ее радиус-вектор , проведенный из начала координат О в точку М, т.е. (рис. 3.1).

При движении точки М вектор будет с течением времени изменяться по модулю и по направлению, т.е. он будет вектор-функцией, зависящей от аргумента : . (3.1) Уравнение (3.1) определяет закон движения материальной точки в векторной форме. Непрерывная линия, которую описывает движущаяся точка относительно

Рис. 3.1.

данной системы отсчета, называется траекторией точки. Если траекторией точки является прямая линия, движение точки называется прямолинейным, а если кривая – криволинейным.

При векторном способе задания движения траектория точки представляет собой годограф радиуса-вектора .

Введением радиуса-вектора, определяющего положение точки, мы не связываем себя с конкретной системой координат, что позволяет широко использовать задание радиуса-вектора как функции времени для получения основных кинематических характеристик движения. Для решения же конкретных задач обычно переходят от векторного способа к координатному и естественному способам задания движения.

3.1.2. Координатный способ задания движения заключается в представлении координат точки в виде известных, непрерывных, дважды дифференцируемых функций времени. Выбор конкретной системы координат определяется содержанием решаемой задачи. Предпочтительнее та система координат, использование которой наиболее целесообразно для данной задачи.

В прямоугольной декартовой системе координаты точки М (рис. 3.1) задаются как известные функции времени, т.е.

, , . (3.2)

Уравнения (3.2) движения точки представляют одновременно и уравнения траектории в параметрической форме, где роль параметра играет время . Если требуется определить уравнение траектории в координатной форме, то нужно исключить каким-либо образом из этих уравнений время .

Во многих случаях бывает предпочтительнее использовать цилиндрические или сферические координаты.

В цилиндрических координатах (рис. 3.2 а) положение точки определяется радиусом , углом (азимут) и аппликатой . Следовательно, движение будет задано, если , , и z будут известными функциями времени

, , . (3.3)

Рис. 3.2.

В сферических координатах (рис. 3.2 б) положение точки определяется полярным радиусом , углом и углом (полюсный угол). Движение будет задано, если

, , (3.4)

– известные функции времени.

Формулы, связывающие цилиндрические и сферические координаты с декартовыми, соответственно будут

, , ;

, , .

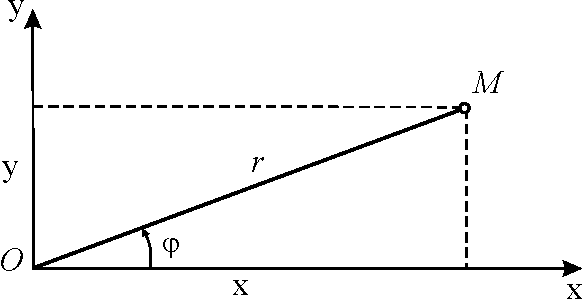
При движении точки в плоскости иногда целесообразно использовать полярные координаты. В этом случае нужно задать в виде функций времени координаты и (рис. 3.3): , .

Рис. 3.3.

Связь этих координат с декартовыми дается формулами

, .

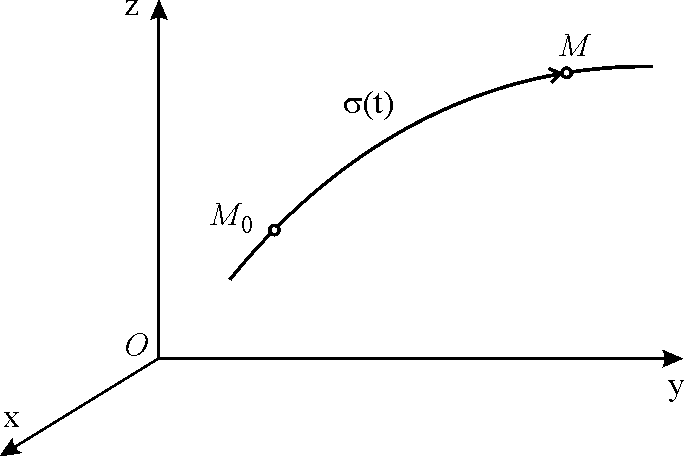
3.1.3. Естественный способ. При естественном способе задания движения указываются (рис. 3.4):

• траектория точки;

• закон движения точки по траектории

; (3.5)

• начало отсчета (точка М₀ на рис. 3.4);

• направление положительного отсчета дуги по траектории.

Рис. 3.4.

Если движение происходит в сторону возрастания дуги , то дифференциал дуги , если же движение происходит в сторону убывания дуги, то дифференциал дуги будет .

Путь s, проходимый точкой, всегда будет возрастать и, следовательно, положителен, т. е.

.

Естественным способом задания движения удобно пользоваться, когда траектория точки заранее известна.

Все рассмотренные способы задания движения взаимосвязаны.

Рис. 3.5.

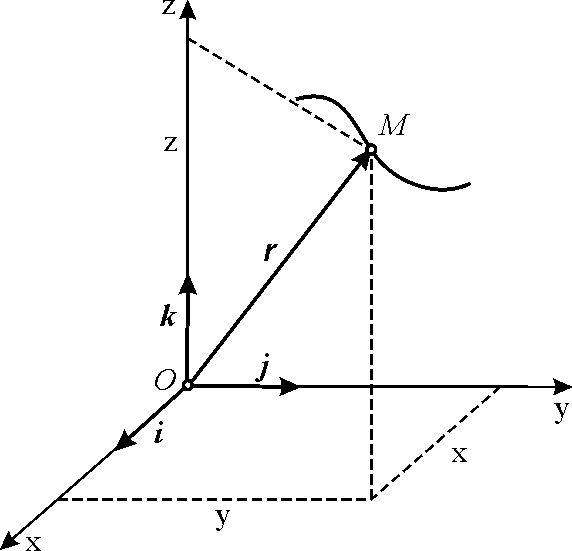
Пусть, например, движение задано координатным способом в виде (3.2). Очевидно, что при этом проекции радиуса-вектора (рис. 3.5) на оси координат равны координатам точки М и, следовательно, можно записать . (3.6) Модуль найдется по формуле

, (3.7)

а направление определится направляющими косинусами

, , . (3.8)

Рис. 3.6.

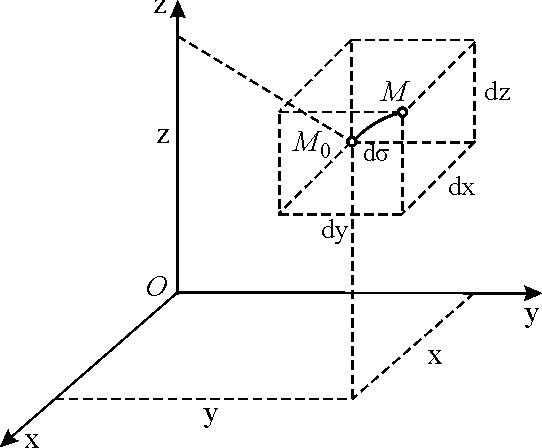
От задания движения в декартовых координатах можно перейти к его заданию естественным способом. Закон движения точки по траектории в дифференциальной форме выражается через декартовы координаты в виде (рис. 3.6)

Интегрируя это выражение в промежутке от (начало движения) до какого-либо момента времени , получим закон движения

.

Знак «плюс» или «минус» перед интегралом ставится в зависимости от выбора направления положительного отсчета дуги; если движение точки начинается в сторону выбранного положительного отсчета дуги, то следует брать знак «плюс», в противном случае – знак «минус».