4. Модели линейного программирования Общая линейная распределительная задача

Пусть предприятие может изготавливать изделия трех наименований П1, П2, П3. Известно, что для изготовления каждого изделия требуется три вида ресурсов, Объемы выпуска продукции измеряются в рублях.

Характеристики	Виды продукции			Располагаемые ресурсы
	П1	П2	П3
Объем выпуска продукции	7	12	13
Ресурсы:
Трудовые	0,2	0,3	0,4	35
Материальные	0,5	0,4	0,3	42
Финансовые	0,6	0,8	1,2	100

Математическая модель задачи:

О б = 7х₁ + 12х₂ + 13х₃ max

0,2х₁ + 0,3х₂ + 0,4х₃ < 35

0,5х₁ + 0,4х₂ + 0,3х₃ < 42

0,6х₁ + 0,8х₂ + 1,2х₃ < 100

х_j  0 , j = 1,3.

Будем характеризовать работу производства двумя параметрами: объемом выпуска продукции и ее качеством. Оценивать качество выпускаемой продукции одним числом очень трудно, а иногда невозможно. Для иллюстрации методов многопараметрической оптимизации примем, что качество оценивается трудоемкостью, измеряемой в единицах человеко-времени.

Таблица 1

Характеристики	Виды продукции			Располагаемые ресурсы
	П1	П2	П3
Объем выпуска продукции	7	12	13
Качество продукции	9	7	10
Ресурсы:
Трудовые	0,2	0,3	0,4	35
Материальные	0,5	0,4	0,3	42
Финансовые	0,6	0,8	1,2	100

Требуется найти планы, оптимальные в смысле многопараметрической оптимизации.

1. Метод последовательных уступок

Суть метода заключается в том, что один из оптимизируемых параметров принимается в качестве целевой функции и задаются некоторые предельные значения граничных условий. Задача решается в нескольких вариантах, которые отличаются друг от друга предельно задаваемыми значениями.

Задавая в качестве целевой функции максимизацию объема выпуска продукции при условии, что показатель ее качества должен быть не меньше заданного значения, получим:

О б = 7х₁ + 12х₂ + 13х₃ max

9х₁ + 7х₂ + 10х₃  К_зад.

0,2х₁ + 0,3х₂ + 0,4х₃ < 35

0,5х₁ + 0,4х₂ + 0,3х₃ < 42

0,6х₁ + 0,8х₂ + 1,2х₃ < 100

х_j  0 , j = 1,3.

Результаты решения этой задачи для различных К_зад. приведены в таблице 2.

Таблица 2

Характеристика	Вариант
	1	2	3
К зад.	Неограничен	900	970
К	830	900	970
Об	1340	1284	1198
П 1	0	14	347
П 2	90	62	29,5
П 3	20	34	47,8
Резерв ресурсов:
Трудовых	0	0	0,7
Материальных	0	0	0
Финансовых	4	1,2	0

Выводы:

1. Повышение требований к качеству продукции приводит к уменьшению объема ее выпуска.

2. В зависимости от требований к качеству продукции меняется структура плана.

3. Дальнейший рост выпуска продукции лимитируется ресурсами.

Возможна другая постановка задачи. Можно максимизировать качество продукции при наложении ограничений на объем ее выпуска, Математическая модель будет иметь вид:

К ₁=9х₁ + 7х₂ + 10х₃ max

7х₁ +12х₂ +13х₃  Об зад.

0,2х₁ + 0,3х₂ + 0,4х₃ < 35

0,5х₁ + 0,4х₂ + 0,3х₃ < 42

0,6х₁ + 0,8х₂ + 1,2х₃ <100

х_j  0, j=1,3

Результаты решения задачи при различных значениях Об_зад. – в таблице 3.

Выводы:

1. Структура плана меняется.

2. Повышение качества лимитирует ресурсы.

3. При реализации требований по увеличению объема выпуска ухудшается качество продукции.

4. В варианте 6 достигнуто полное использование всех ресурсов. При этом качество продукции оказывается на самом низком уровне.

Таблица 3

Характеристики	Вариант
	4	5	6
Об зад.	Неограничен	1180	1260
Об	1108	1180	1260
К	1028	981	930
П 1	48,6	35	20
П 2	0	23,8	50
П 3	59	50	40
Резерв ресурсов:
трудовых	1,7	0,9	0
Материальных	0	0	0
финансовых	0	0	0

Объединив результаты расчетов, можно построить зависимость объемов выпуска продукции от ее качества.

Значения Об расставлен по мере возрастания качества К продукции.

Вариант	1	2	6	3	5	4
К	830	900	930	970	981	1028
Об	1340	1284	1260	1198	1180	1108

Можно построить графически:

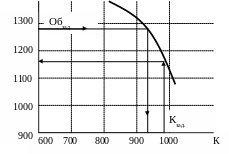
3. Многопараметрическая оптимизация

Многопараметрическая оптимизация представляет собой попытку найти некоторый компромисс между теми параметрами, по которым требуется оптимизировать решение.

Возможной реализацией такого компромиссного подхода является формирование специальной целевой функции.

Два метода, обеспечивающие получение компромиссных решений:

а) компромиссная целевая функция;

б) оптимизация в смысле многоцелевого программирования.

а) Компромиссная целевая функция

КЦФ должна удовлетворять следующим требованиям:

1. приведение параметров, имеющих, как правило, различную размерность, к безразмерной форме;

2. возможность назначения относительной важности каждого параметра, что и определяет компромисс;

3. увеличение значения целевой функции для улучшающих параметров и уменьшение для ухудшающих параметров.

Пример целевой функции, удовлетворяющей этим требованиям:

К - количество параметров, по которым производится оптимизация;

- нормирующая величина, обеспечивающая безразмерность параметров;

- коэффициент веса, задающие степень компромисса.

Значение величины можно назначать различными способами. Наиболее распространены два способа.

В первом случае , где принимается из утвержденного документа, например, технического задания.

Во втором случае, если заданной величины нет, можно решить задачу при максимизации этой величины:

Полученное в результате оптимизации значения принять за нормирующее, т.е .

Коэффициенты веса назначаются при обеспечении условия с помощью экспертных оценок, получение которых мы уже рассмотрели.

Рассмотрим на примере прежней задачи. Оптимизация проводится по двум параметрам: объему и качеству выпускаемой продукции. Целевую функцию можно записать следующим образом:

В качестве нормирующих значений принимаем их максимальные значения, полученные в результате оптимизации отдельно по каждому параметру:

Об_н =1340

К_н =1028

Получим модель:

Об =7х₁ + 12х₂ + 13х₃

К =9х₁ + 7х₂ + 10х₃

0,2х₁ + 0,3х₂ + 0,4х₃ < 35

0,5х₁ + 0,5х₂ + 0,3х₃ < 42

0,6х₁ + 0,8х₂ + 1,2х₃ < 100

х_j0, j = 1,3.

Результатом решения этой задачи при различных значениях коэффициентов ₁ и ₂ приведены в таблице 4.

Таблица 4

Характеристика	Вариант
	1	2	3
1	1,0	0,5	0
2	0	0,5	1,0
Е	100	94,4	100
Об	1340	1260	1108
К	830	930	1028
П 1	0	20	49
П 2	90	50	0
П 3	20	40	59
Резерв ресурсов:
трудовых	0	0	1,7
материальных	0	0	0
финансовых	4	0	0

Выводы:

1) Применительно к объему выпуска наиболее выгодна продукция П 2. По мере снижения коэффициента веса ₁ ее выпуск уменьшается. Самая невыгодная – П1, которая при ₁ =1,0 вообще не выпускается.

2) Наиболее выгодной с позиции качества является продукция П1, наиболее невыгодной П2, которая при ₂ = 1,0 не выпускается.

3) Для обеспечения дальнейшего роста объема выпуска продукции необходимо увеличить ресурсы трудовые и материальные, а для повышения качества продукции – ресурсы материальные и финансовые.

б) Метод многоцелевого программирования

Решается задача последовательно по двум целевым функциям: максимизации объема и максимизации качества.

Получим результаты, согласно которым при располагаемых ресурсах максимально возможные значения объема выпуска и качества продукции соответственно равны 1340 и 1028. Одновременно такие значения получены быть не могут.

Примем, что необходимо обесп6ечить одновременно выполнение экономических показателей

Об = 1500

К = 1100

Очевидно, что при имеющихся ресурсах такие показатели не могут быть достигнуты. Данная задача является несбалансированной между заданными экономическими показателями и располагаемыми ресурсами.

Математическая модель:

Об = 7х₁ + 12х₂ + 13х₃= 1500

К = 9х₁ + 7х₂ + 10х₃= 1100

0,2х₁ + 0,3х₂ + 0,4х₃ < 35

0,5х₁ + 0,5х₂ + 0,3х₃ < 42

0,6х₁ + 0,8х₂ + 1,2х₃ < 100

х_j0, j = 1,3.

Решения у данной задачи нет (имеет несовместное решение).

Кроме того, в рассматриваемой системе нет целевой функции.

Для получения совместного решения, а также назначения целевой функции введем дополнительные переменные у₁-у₈ и заменим систему в виде

Об = 7х₁ + 12х₂ + 13х₃ + у₁ = 1500

К = 9х₁ + 7х₂ + 10х₃ + у₂ = 1100

0,2х₁ + 0,3х₂ + 0,4х₃ + у₃ = 35+у₆

0,5х₁ + 0,5х₂ + 0,3х₃ + у₄ = 42+у₇

0,6х₁ + 0,8х₂ + 1,2х₃ + у₅ = 100+у₈

Смысл дополнительных переменных:

у₁, у₂ - показывают, насколько полученные значения объема выпуска и качества продукции отличаются от заданных;

у₃, у₄, у₅ - определяют неиспользованный ресурс;

у₆, у₇, у₈ - равны значениям дополнительного ресурса, которые необходимо иметь для решения поставленной задачи.

Эти переменные являются тем средством, которое дает возможность избежать получения несовместного решения.

Введенные дополнительные переменные позволяют формулировать различные многопараметрические функции.

Рассмотрим две из них:

1) Е₁=у₁ + у₂  min

обеспечивает решение, гарантирующее выполнение двух заданных экономических показателей: объема выпуска и качества продукции.

3) Е₂= у₆ + у₇ + у₈  min

позволяет получить решение, при котором дополнительные ресурсы будут минимальными.

Результаты решения:

Характеристики	Целевая функция
	Е1	Е2
Е	0	0
Об	1500	1260
К	1100	930
П1	45,8	20
П2	98,3	50
П3	0	40
у1	0	240
у2	0	170
у3	0	0
у4	0	0
у5	0	0
у6	3,6	0
у7	20,2	0
у8	6,1	0

Общая форма записи задачи может быть представлена как:

j=1, n i=1, m p=1,p

После введения дополнительных переменных эту систему запишем в виде:

j=1, n i=1, m p=1,p

Целевая функция может быть сформулирована следующим образом:

где m+p - число параметров, по которым ведется оптимизация;

_i - коэффициент веса, определяющий уровень компромисса между оптимизируемыми параметрами;

y_i - дополнительные переменные, вводимые в целевую функцию;

b_i - нормирующий элемент, аналогичный в компромиссной целевой функции.

Если нет каких-либо ограничений, исключающих получение значения y_i = 0 (как это было в рассмотренных примерах), то величину b_i можно не вводить. Если же в решении y_i = 0 не может быть достигнуто, то следует вводить b_i.

Контрольные вопросы самопроверки

1. Предложите ситуацию, в которой следует использовать модели теории очередей.

2. Предложите ситуацию, в которой следует использовать модели управления запасами.

3. Предложите ситуацию, в которой эффективно использование задачи о двух машинах.