2 Властивості алгоритму
Алгоритм повинен мати такі властивості:
Дискретність — процес розв'язку розбивається на кроки. Кожен крок — це одна дія або підпорядкований алгоритм (метод покрокової деталізації). Таким чином, полегшуєть-ся процес знайдення помилок і редагування алгоритму.
Визначеність (точність) — кожен крок алгоритму має бути однозначно описаною дією і не містити двозначностей.
Зрозумілість — усі дії, включені до алгоритму, мають бути у межах компетенції виконавця алгоритму.
Універсальність (масовість) — алгоритм має виконуватися при будь-яких значеннях вхідних даних та початкових умов.
Скінченність — алгоритм має бути реалізований за скінче-не число кроків і повинен користуватися скінченим набором вхідних значень.
Результативність — алгоритм має привести до отримання результату. Якщо алгоритму присутні перелічені вище властивості, то його виконання провадиться формально, тобто точно за схемою алгоритму, без будь-яких втручань у послідовність дій та у самі дії.
3 Способи опису алгоритмів
Етап розв'язування задачі, результатом якого є розробка алгоритму її розв'язання, називається алгоритмізацією (під цим розуміють зведення розв'язування задачі до ланцюжка простих кроків, які виконуються послідовно один за одним).
У широкому розумінні алгоритмізація складається з вибо-ру методу розв'язування задачі та форми представлення вхідної інформації, які враховують специфіку комп'ютера.
Розроблений алгоритм можна зафіксувати трьома спосо-бами :
людською мовою;
у вигляді схем;
3) у вигляді програми, тобто за допомогою специфічної мови для запису алгоритмів, яка є зрозумілою для комп'ютера (на алгоритмічній мові). Один і той же алгоритм можна записати на різних алгоритмічних мовах.
Найчастіше алгоритми обчислювальних процесів подаються у вигляді блок-схем, де кожний крок алгоритму представлений спеціальним блоком, який умовно показує дію, яку треба виконати. Сама дія записується всередину блока і є конкретною для даного алгори-тму.
Блок-схемний метод алгоримізації передбачає розподіл усього обчислювального процесу на окремі кроки, які позначаються графічними зображеннями - «блоками». Блок-схемою алгоритму називається стандартизоване (див. ГОСТ 19.701-90) графічне зображення алгоритму, кожному кроку якого відповідає блок. Звичайне співвідношення розмірів сторін блоку таке, що його довжина становить дві його висоти. Усі блоки, окрім блоків «Початок» і «Кінець», нумерують по струмах зверху-донизу і зліва-направо арабськими цифрами; номер ставлять ліворуч над блоком чи у розриві верхньої лініі блоку.
У блок-схемі може бути присутнім тільки один блок «Початок», з якого починається абиякий алгоритм, і не менше одного блока-термінатора «Кінець», яким завершується виконання алгоритму:
Б
локи
«Введення»
і «Виведення»
використовуються для введення значень
даних, список ідентифікаторів яких вони
містять усередині, із зовнішніх пристроїв
(клавіатури, файлу на дисці і т.і.) або
виведення значень розрахункових даних
на зовнішні пристрої (монітор, принтер,
файл на дисці і т.і.):
Блок «Процес» (див. подальший малюнок, ліворуч) використовується для обчислення даних за формулою, яку записано усередині блоку. Блок «Визначений процес» (див. подальший малюнок, праворуч) використовується для виклику на виконання підпорядкованого алгоритму:
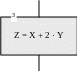
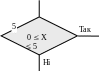
Блок «Рішення» містить усередині умову, яка піддається сумніву; цей блок застосовується для організації розгалужень алгоритму.
Блок «Межа циклу» (типу «початок циклу» - ліворуч, типу «кінець циклу» - праворуч) застосовується для організації й обмеження циклів. Ініціююче значення параметру циклу (наприклад, X = Xn), його кінцеве значення (Xk), крок збільшення чи зменшення (X), або умова завершення циклу (X Xk) записуються усередині початкового чи кінцевого блоку у залежності від типу циклу:
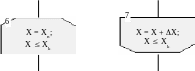
Блок «Модифікація» застосовується для організації ітераційного циклу з передумовою і параметром, що змінюється з деяким кроком. Ініціююче значення, кінцеве значення і крок збільшення чи зменшення параметру циклу записують усередині блоку. Наприклад, запис X=Xn;Xk;X позначає зміну параметру X від початкового значення Xn до кінцевого значення Xk із кроком X:
Блоки у блок-схемі, як правило, мають один горизонтальний розмір, можуть викреслюватися у будь-якій орієнтації і з'єднуються лініями потоку. Ці лінії повинні бути спрямовані до центру блоку і, за звичай, підходять до нього зверху або ліворуч, а виходиять з нього знизу або праворуч.
Лінії потоку закінчуються стрілкою, якщо блоки, що з'єднуються, виконуються у напрямках «ліворуч» чи «нагору», або ж лінія потоку перетерплює злам. Декілька ліній потоку можуть з'єднуватися в одну, причому місце з'єднання звичайно зсовується:
