2. Квадратичные формы поверхности

18. Первая квадратичная форма поверхности и ее положительная определенность

Первая квадратичная форма поверхности по определению есть квадрат дифференциала дуги некоторой кривой на поверхности

I=ds²=dr²=(r_udu+r_vdv)²=(r_ur_u)du²+2(r_ur_v)dudv+(r_vr_v)dv²).

Введем обозначения

(0(r_ur_u)=E, (r_ur_v)=F, (r_vr_v)=G. (0)(2.1( 2 .1)

Тогда для первой квадратичной формы имеем

(0I=Edu²+2Fdudv+Gdv². (0)(2.2( 2 .2)

Если поверхность регулярная, то первая квадратичная форма положительно определенная. Действительно, из условия регулярности поверхности имеем

r_ur_v0 => |r_ur_v|²=|r_u|²|r_v|²−(r_ur_v)²=EG−F²0 или (EG−F²)>0,

что и обусловливает положительную определенность первой квадратичной формы регулярной поверхности.

Обратное утверждение: поверхность с положительно определенной квадратичной формой регулярна – может быть не верным?.

Все кривые на поверхности с положительно определенной квадратичной формой гладкие, так как в этом случае имеем

I=ds²=dr²=(r_uudp+r_vvdp)²=(dr/dp)²dp²0.

Регулярность предполагает такую параметризацию поверхности, при которой исключается возможность равенства нулю величины r_ur_v и если (p) регулярная, то r (p)0. В общем случае на регулярной поверхности может лежать и не регулярная кривая.

19. Угол между кривыми на поверхности. Угол между координатными линиями

Углом между двумя пересекающимися кривыми на поверхности называется угол между их касательными в точке пересечения.

Пусть на поверхности r=r(u,v) имеются две кривые r=r₁(p₁) и r=r₂(p₂).

dr_i=r_ud_iu+r_vd_iv, (i=1,2).

Приращение (дифференциал) du или dv, рассматриваемый в связи с изменением функции r_i, мы будем обозначать с помощью символа d_iu или соответственно d_iv: dr_i=r_id_i, d_i=(d/dp_i)dp_i. (?См. также Выгодский, д/г, стр. 259, хотя и по другому поводу. По этому поводу – стр. 255 обозначения такие – du, u; dv, v?).

Тогда для косинуса одного из углов между этими кривыми будем иметь

cos=(dr₁∙dr₂)/(|dr₁|∙|dr₂|)=

= .

Отсюда видно, что угол определяется внутренними координатами кривых и коэффициентами первой квадратичной формы.

Условие ортогональности кривых в точке их пересечения будет иметь вид

Ed₁ud₂u+F(d₁ud₂v+d₁vd₂u)+Gd₁vd₂v=0.

Выражение слева называется [⁴, с. 311] билинейной квадратичной формой. По Фавару (с. 311) – это «полярная форма для второй квадратичной формы».

Угол между координатными линиями

Пусть координатная линия u=const есть первая кривая r₁, а координатная линия v=const – вторая кривая r₂. Тогда

L₁: u=const, d₁u=0,

L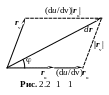 ₂: v=const, d₂v=0.

Тогда для угла  между этими координатными линиями получаем

cos= .

Из этого соотношения, в частности, следует, что ортогональным координатным линиям соответствует нулевое значение второго коэффициента F первой квадратичной формы.

Замечание. Направление на поверхности в некоторой ее точке (u, v) определяется отношением du:dv. Действительно, направление на поверхности можно определить направлением дифференциала dr радиус-вектора r текущей точки поверхности, т.е. вектором dr=r_udu+r_vdv=dv(r_udu/dv+r_v). Так как векторы r_u, r_v в данной точке фиксированы и не зависят от выбора направления, то последнее определяется значением du/dv=du:dv, которое будем обозначать и называть: направление du:dv. (См. рис. Error: Reference source not found).