Формула Эйлера выражающая нормальную кривизну поверхности в заданном направлении через главные кривизны

Из курса линейной алгебры и геометрии известно, что если направления осей координат (координатных линий r_u, r_v в нашем случае) совпадают с главными осями симметрии центральной кривой второго порядка (индикатрисы в нашем случае), то эти оси ортогональны (F=0), а их пересечение с индикатрисой соответствует экстремальным расстояниям точек индикатрисы от ее центра, т.е. экстремальным значениям полярного радиуса точек индикатрисы (радиуса нормальной кривизны) и, следовательно, самой нормальной кривизны (нагляден пример эллипса). Отсюда следует также, что у регулярной поверхности в каждой ее точке существует не менее двух различных направлений, соответствующих экстремальным значениям нормальной кривизны.

Э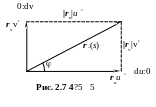 кстремальные значения нормальной кривизны поверхности в данной ее точке называются главными кривизнами поверхности, а соответствующие направления – главными направлениями.

Выразим нормальную кривизну поверхности в данной ее точке в данном направлении через главные кривизны в этой точке.

Короткий вывод этой формулы см. также [¹⁶, стр. 190, 244] и [¹⁷, с. 198], [Шикин. Первое знакомствоError: Reference source not found¹⁸].

К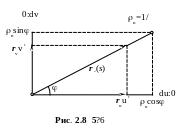 ак мы уже знаем, нормальная кривизна и угол между двумя направлениями на касательной плоскости поверхности в некоторой фиксированной ее точке не зависят от параметризации поверхности. Тогда для простоты, не меняя общности, параметризацию будем считать такой, что направления координатных линий в данной точке поверхности совпадают с главными направлениями в этой точке. (Если направление кривой во всех ее точках совпадает с главным направлением, то такие кривые называют линиями кривизны, которые мы будем рассматривать далее). Тогда, переходя с помощью преобразований поворота в уравнении (0) индикатрисы к главным центральным осям, получим уравнение, в котором слагаемое, содержащее произведение абсциссы и ординаты, будет отсутствовать. Будет отсутствовать соответствующее слагаемое и в (0) [?], которое примет вид

(0k()=cos²+sin². (0)(3.15( 3 .15)

Так как коэффициенты ,  не зависят от , то полагая последовательно =0 и =/2, найдем =k(0)=k₁, =k(/2)=k₂. Тогда (0) примет вид формулы Эйлера (0).

(0k_n=k₁cos²+k₂sin². (0)(3.16( 3 .16)

Или так…?

…F=M=0 (это, по-видимому, следует приводить после характ. ур-я?).

И уравнение (0) индикатрисы примет вид

|(L/E)²+(N/G)²|=1.

Экстремальному значению полярного радиуса точек индикатрисы по направлению оси абсцисс (=0) соответствует величина k₁=L/E, по оси ординат (=/2) – величина k₂=N/G.

k₁=L/E, k₂=N/G.

Тогда уравнение индикатрисы примет вид |k₁²+k₂²|=1.

Обозначим через  угол, который направление du:dv образует с первым главным направлением du:0. Получим

cos=/=/(²+²)^1/2= u, sin=/=/(²+²)^1/2= v, ²+²=k_n.

Из общей формулы для нормальной кривизны будем иметь

k_n=II/I=(Ldu²+2Mdudv+Ndv²)/(ds²)=

=Lu²+Nv²=k₁Eu²+k₂Gv².

Отсюда с учетом того, что

|r(s)|= = =1,

или из уравнения индикатрисы для нормальной кривизны получаем формулу Эйлера в виде (0)

(0k_n=k₁cos²+k₂sin². (0)(3.17( 3 .17)

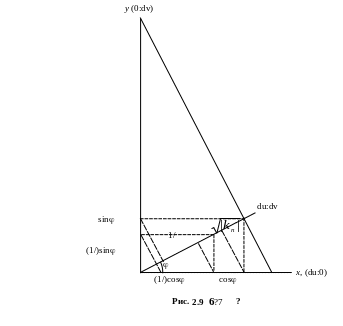
Геометрическая интерпретация соотношения (0)( 3 .17)? рассматривается в книгах [¹⁹, с. 37], [²⁰, c. 241], а также в статье [²¹].

[Error: Reference source not found], cтр. 37: Круг Мора, позволяющий определять условия предельного равновесия вдоль площадки сдвига 4_xy²+(_x−_y)²=(_x+_y+2cctg)2sin².

[^{22Error: Reference source not found}], с. 241: Выражения =₁cos²+₃sin², =(₁−₃)sincos можно переписать в виде

=(₁+₃)/2+(₁−₃)/2cos2+₃sin², =(₁−₃)/2sin2.