3.2. Формулы

Пусть имеется некоторое подмножество BP_{2 .}

Определение. Формулой над множеством называется выражение вида:

1) , если ;

2) , если , а– либо формула над, либо переменнаяиз нашего алфавита, где.

При этом никаких других формул над нет.

Пример: Пусть . Рассмотрим следующее выражение:, которое является формулой над, так как:

1. – формулы по определению.

2. – вместоподставляем– значит, формула.

3. – тоже формула.

Формулы удобно обозначать с помощью деревьев:

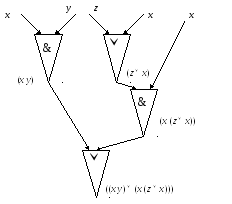
3.3. Сопоставление формулам над множеством функций

Определение. 1) Если формула есть выражение вида , где , то формуле соответствует функция .

2) Если формула есть выражение вида , где ,

а) – формула над, то выражениюсопоставлена функция ;

б) – переменная, тосопоставлена тождественная функция .

Тогда формуле вида сопоставим функцию .

Определение. Если формуле сопоставлена функция, то говорят, что формулареализует функцию. Тогда функциюназываютсуперпозицией функций из множества , а процесс получения функциииз функций множествабудем называтьоперацией суперпозиции.

Определение. Формулы иG называются эквивалентными (ФG), если они реализуют одинаковые функции.

Пример: Пусть .

Тогда Ф = (((x₁x₂)+x₁)+x₂) является формулой над , она строится за три шага. Мы имеем следующие подформулы,,.

Формуле соответствует функция, она определяется следующим образом:

0 0 0 1 1 0 1 1	0 0 0 1	0 0 1 0	0 1 1 1

Очевидно, что .

Пример: Пусть даны формулы Ф=(x→y), G=(). ФG?

x y
0 0 0 1 1 0 1 1	1 1 0 1	1 0 1 0	1 1 0 0	1 1 0 1

Формулы иG эквивалентны, так как реализуют одинаковые функции.

3.4. Свойства элементарных функций

1. – коммутативность (аналогичным свойством обладают и «», «»,«»,«»,«»).

2. – ассоциативность (аналогичным свойством обладают «», «»,«»).

3.

–дистрибутивные законы

(y+z))=y)+z).

4. .

5. ,– законы де Моргана.

6.

Замечание. Тождества могут быть проверены путем сопоставления функций, соответствующих правой и левой частям тождеств.

Замечание. С целью упрощения записи формул мы условимся, что операция сильнее операции.

7. Правило поглощения:

а) , где–формула.

Доказательство: .

б) , где–формула.

Доказательство: .

8. Правило склеивания:

а) , где–формула.

Доказательство: .

б) , где–формула.

Доказательство:

.

9. Правило обобщенного склеивания:

а) , где–формулы.

б) , где–формулы.

а) и б) доказать самостоятельно.

3.5. Разложение булевых функций

Теорема 2. Каждая функция из может быть представлена следующим образом:

1. ,

2. ,

3. .

Доказательство пункта 1: Возможны два случая:

1) , тогда .

2) , тогда

Аналогично доказываются пункты 2 и 3.

Теорема 3. Каждая функция из при, представима в виде:

1.,

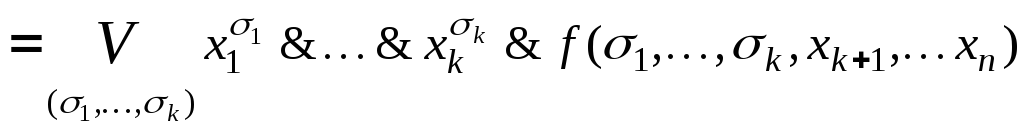где

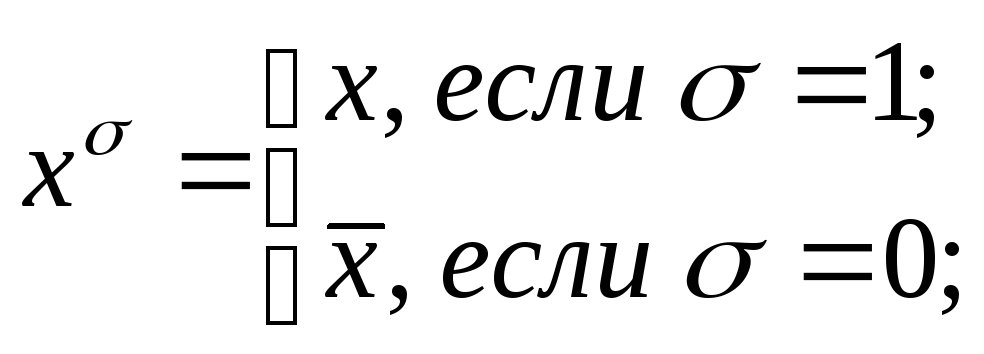
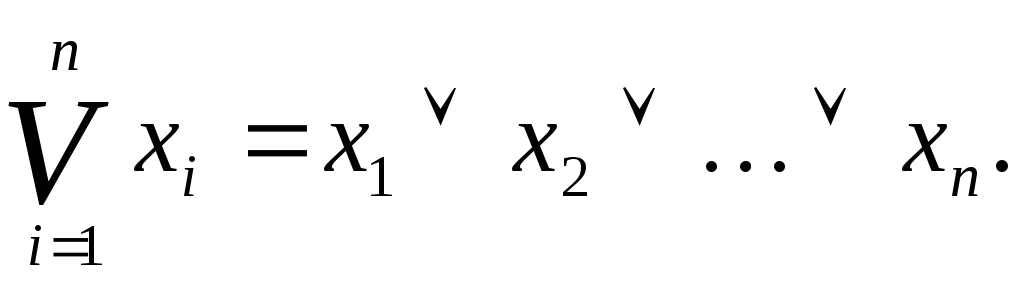
2., где

3. ,

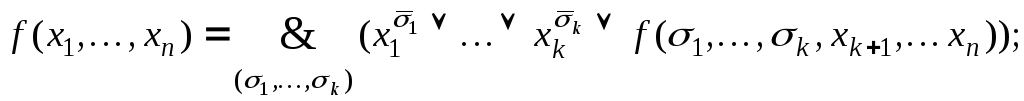где ,

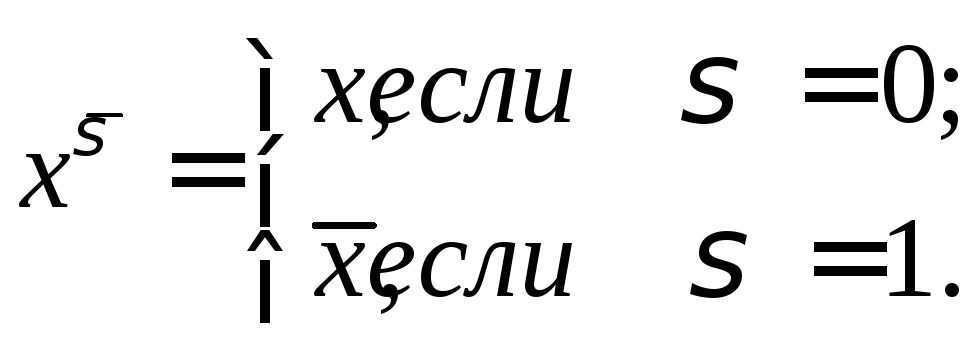
Доказательство пункта 1: Рассмотрим произвольный набор длины .

Слева мы имеем .

Учтем, что

по определению,

а это означает, что .

Так как , значит,равна нашей формуле в том и только в том случае, когда.

Отсюда 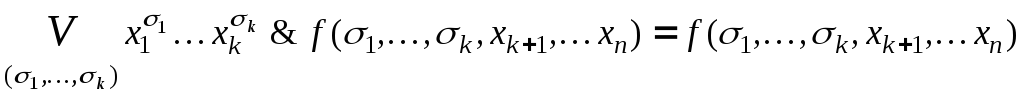– это справа, так как остальные конъюнкции = 0. А слева мы получаем то же выражение, потому что . Итак, .

Пункты 2 и 3 доказываются аналогично.