Продолжение таблицы 5
Т
аблица
6
Значения 2 решения уравнения
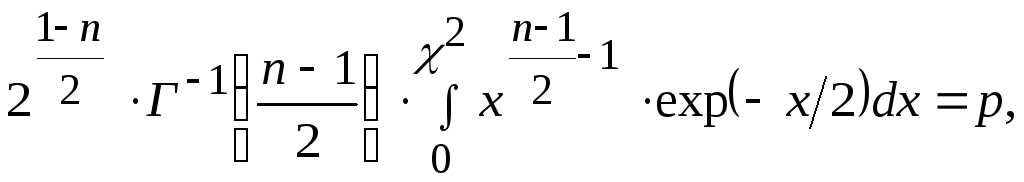
для
левого конца интервала при 2р
= 1-,
значение
для
правого конца интервала при р=1-(1-)/2,
значение
|
r |
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27 28 29 30 |
0,000 0,020 0,115 0,297 0,554 0,872 1,239 1,646 2,09 2,56 3,05 3,57 4,11 4,66 5,23 5,81 6,41 7,02
7,63 8,26 8,90 9,54 10,20 10,86 11,52 12,20 12,88 13,56 14,26 14,95 |
0,001 0,040 0,185 0,429 0,752 1,134 1,564 2,03 2,53 3,06 3,61 4,18 4,76 5,37 5,98 6,61 7,26 7,91
.8,57 9,24 9,92 10,60 11,29 11,99 12,70 13,41 14,12 14,85 15,57 16,31 |
0,004 0,103 0,352 0,711 1,145 1,635 2,17 2,73 3,32 3,94 4,58 5,23 5,89 6,57 7,26 7,96 8,67 9,39
10,11 10,85 11,59 12,34 13,09 13,85 14,61 15,38 16,15 16,93 17,71 18,49 |
0,016 0,211 0,584 1,064 1,610 2,20 2,83 3,49 4,17 4,86 5,58 6,30 7,04 7,79 8,55 9,31 10,08 10,86
11,65 12,44 13,24 14,04 14,85 15,66 16,47 17,29 18,11 18,94 19,77 20,6 |
0,064 0,446 1,005 1,649 2,34 3,07 3,82 4,59 5,38 6,18 6,99 7,81 8,63 9,47 10,31 11,15 12,00 12,86
13,72 14,58 15,44 16,31 17,19 18,06 18,94 19,82 20,7 21,6 22,5 23,4 |
0,148 0,713 1,424 2,20 3,00 3,83 4,67 5,53 6,39 7,27 8,15 9,03 9,93 10,82 11,72 12,62 13,53 14,44
15,35 16,27 17,18 18,10 19,02 19,94 20,9 21,8 22,7 23,6 24,6 25,5 |
0,455 1,386 2,37 3,36 4,35 5,35 6,35 7,34 8,34 9,34 10,34 11,34 12,34 13,34 14,34 15,34 16,34 17,34
18,34 19,34 20,3 21,3 22,3 23,3 24,3 25,3 26,3 27,3 28,3 29,3 |
1,074 2,41 3,66 4,88 6,06 7,23 8,38 9,52 10,66 11,78 12,90 14,01 15,12 16,22 17,32 18,42 19,51 20,6
21,7 22,8 23,9 24,9 26,0 27,1 28,2 29,2 30,3 31,4 32,5 33,5 |
1,642 3,22 4,64 5,99 7,29 8,56 9,80 11,03 12,24 13,44 14,63 15,81 16,98 18,15 19,31 20,5 21,6 22,8
23,9 25,0 26,2 27,3 28,4 29,6 30,7 31,8 32,9 34,0 35,1 36,2 |
2,71 4,60 6,25 7,78 9,24 10,64 12,02 13,36 14,68 15,99 17,28 18,55 19,81 21,1 22,3 23,5 24,8 26,0
27,2 28,4 29,6 30,8 32,0 33,2 34,4 35,6 36,7 37,9 39,1 40,3 |
3,84 5,99 7,82 9,49 11,07 12,59 14,07 15,51 16,92 18,31 19,68 21,0 22,4 23,7 25,0 26,3 27,6 28,9
30,1 31,4 32,7 33,9 35,2 36,4 37,7 38,9 40,1 41,3 42,6 43,8 |
5,41 7,82 9,84 11,67 13,39 15,03 16,62 18,17 19,68 21,2 22,6 24,1 25,5 26,9 28,3 29,6 31,0 32,3
33,7 35,0 36,3 37,7 39,0 40,3 41,7 42,9 44,1 45,4 46,7 48,0 |
6,64 9,21 11,34 13,28 15,09 16,81 18,48 20,1 21,7 23,2 24,7 26,2 27,7 29,1 30,6 32,0 33,4 34,8
36,2 37,6 38,9 40,3 41,6 43,0 44,3 45,6 47,0 48,3 49,6 50,9 |
10,83 13,82 16,27 18,46 20,5 22,5 24,3 26,1 27,9 29,6 31,3 32,9 34,6 36,1 37,7 39,3 40,8 42,3
43,8 45,3 46,8 48,3 49,7 51,2 52,6 54,1 55,5 56,9 58,3 59,7 |
p
1
Продолжение
таблицы 6
Таблица 7
Значения
удовлетворяющие равенству
,
в зависимости от
иn-1
|
n-1 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
n-1 |
|
2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
|
0,158 142 137 134 132
131 130 130 129 129
129 128 128 128 128
128 128 127 127 127
|
0,325 289 277 271 267
265 263 262 261 260
260 259 259 258 258
258 257 257 257 257
|
0,510 445 424 414 408
404 402 399 398 397
396 395 394 393 393
392 392 392 391 391 |
0,727 617 584 569 559
553 549 546 543 542
540 539 538 537 536
535 534 534 533 533 |
1,000 0,816 765 741 727
718 711 706 703 700
697 695 694 692 691
690 689 688 688 687
|
1,376 1,061 0,978 941 920
906 896 889 883 879
876 873 870 868 866
865 863 862 861 860 |
1,963 1,336 1,250 1,190 1,156
1,134 1,119 1,108 1,100 1,093
1,088 1,083 1,079 1,076 1,074
1,071 1,069 1,067 1,066 1,064 |
3,08 1,886 1,638 1,533 1,476
1,440 1,415 1,397 1,383 1,372
1,363 1,356 1,350 1,345 1,341
1,337 1,333 1,330 1,328 1,325 |
6,31 2,92 2,35 2,13 2,02
1,943 1,895 1,860 1,833 1,812
1,796 1,782 1,771 1,761 1,753
1,746 1,740 1,734 1,729 1,725 |
12,71 4,30 3,18 2,77 2,57
2,45 2,36 2,31 2,26 2,23
2,20 2,18 2,16 2,14 2,13
2,12 2,11 2,10 2,09 2,09 |
31,8 6,96 4,54 3,75 3,36
3,14 3,00 2,90 2,82 2,76
2,72 2,68 2,65 2,62 2,60
2,58 2,57 2,55 2,54 2,53 |
63,7 9,92 5,84 4,60 4,03
4,71 3,50 3,36 3,25 3,17
3,11 3,06 3,01 2,98 2,95
2,92 2,90 2,88 2,86 2,84 |
63,7 31,6 12,94 8,61 6,86
5,96 5,40 5,04 4,78 4,59
4,49 4,32 4,22 4,14 4,07
4,02 3,96 3,92 3,88 3,85 |
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20 |
1