2.3.5.2 Непрерывные цепи Маркова

Если система с конечным или счетным числом состояний может переходить из одного состояния в другое в любой момент времениt, то будем говорить, что заданацепь Марковаснепрерывнымвременем.

Определение. Случайный процессtобразуетнепрерывную цепьМаркова, если для произвольной последовательности,i= 1, 2, …,n, такой, чтоt₀t₁…t_n, выполняется

. (76)

Это определение является непрерывным аналогом определения (66). Интерпретация та же самая: состояние системы Sв будущем зависит только от

текущего ее состояния (настоящего) и не зависит от того, как и когда система попала в это состояние.

Определение. Цепи Маркова, сформулированные в терминах случайных процессов, называются марковскими процессами.

Рассмотренные здесь цепи Маркова - суть марковские процессы.

Непрерывные марковские процессы отличаются от дискретных тем, что случайные изменения состояний системы зависят от непрерывно изменяющихся параметров.

Пусть задан процесс (t), определяющий состяние ситемы в момент времениtT. Зададим процесс ее развития: если, в данный момент времени(<t), система находится в состоянииi, то в последующий момент времениtона будет находится в состоянииjс вероятностью, независимо от поведения системы до момента. Для такой системы вероятности

,,

называются переходными вероятностямимарковского процесса.

Определение.Марковский процесс(t)называетсяоднородным, если переходные вероятностизависят только от разности (t-), то есть

.

В общем случае вместо переходных вероятностей можно рассматривать соответствующие плотности вероятностей. В качестве примера, можно привести броуновское движение, распространенное на непрерывный случай (Винеровский процесс 2).

2.3.5.3 Потоки событий

Потоком событийназывается появление однородных событий в случайные моменты времени.

Рис. 29

Рассмотрим временную ось (рис. 29). Поток событий представляет собой, вообще говоря, последовательность случайных точек ₁₂…_nна оси, разделенных временными интерваламиТ_i =_i+1_i),iN, длина которых случайна.

Потоки событий различаются по законам распределения длин интервалов T_i между событиями, по их зависимости или независимости, регулярности и др.

Наиболее изучены потоки, которые обладают следующими свойствами:

а) стационарность– все его вероятностные характеристики не меняются со временем;

б) отсутствие последействия– для любых непересекающихся временных интервалов на временной оси, число событий, находящихся на одном интервале,не зависитот того, сколько их и как они оказались на другом интервале;

в) ординарность – практическая невозможность на достаточно малом временном интервале появиться двум и более событиям.

Для формализации этих свойств, введем понятие интенсивности.

Пусть - вероятность того, что за времяt, примыкающего к моменту времениt, появилосьiсобытий,iN.

Рассмотрим полную группу несовместных событий, для которой, по определению, имеем

. (77)

Введем обозначение, пусть - вероятность того, что за времяtпоявилось более одного события.

Тогда формула (77) примет вид

. (78)

Из определения ординарности следует, что

, (79)

где 0(t) – бесконечно малая более высокого порядка, чем наименьшая из вероятностейи, то есть.

Обозначим через математическое ожидание числа событий появившихся за время, тогда, по определению,

.

С учетом ординарности и свойств бесконечно малой, имеем

или

Положим

Определение. Функцияпараметраtназываетсяинтенсивностью (плотностью) ординарного потока событий в моментt, если

. (80)

Стандартная трактовка -среднее число событий, приходящихся на единицу времени, для участка, примыкающего к моментуt.

Ясно, что , и имеет размерность обратную времени -.

Пример. Среднее число событий ординарного потока, на интервале длиной, примыкающего кt, равно

, (81)

в частности, для стационарного потока, имеем

Наконец, отсутствие последействияформулируется следующим образом.

Пусть вероятность того, что за время, примыкающего к моменту времениt, появилоськсобытий при условии, что в момент времениtбылоn-ксобытий. Тогда условие отсутствия последействия означает, что

,к= 0, 1, …,n. (82)

В частности, при tик= 1, имеем

. (83)

Замечание. Формула (82) в терминах биологии может интерпретироваться как вероятность роста популяции [6] накединиц за время. Аналогично, имеет смысл говорить о гибели популяции нак единиц за время, если в моментtпопуляция состояла из (n+k) единиц, то есть

.

Определение. Поток событий называетсяпростейшим,если он обладает свойствами:

а) стационарности: =const,

б) отсутствия последействия:

.

в) ординарности:

.

Замечание. Простейший поток событий является достаточно общим, в том смысле, что получаемые вероятностные характеристики функционирования систем в условиях простейшего потока, как правило, наиболее пессимистичны, то есть «хуже не будет».

Покажем что, если поток событий простейший, то распределение длин интервалов между поступлениями любой пары соседних событий показательное (экспоненциальное) с плотностью

,,(84)

Следующие постулаты сразу следуют из определения простейшего потока:

1. для всякого малого t0, существует ненулевая вероятность появления события;

2. если система начинает функционировать с момента t= 0, то первое появление события имеет место в моментt0.

Рассмотрим функцию

. (85)

если - плотность, то

.

Из свойства отсутствия последействия, имеем

,,. (86)

Вычитая из обеих частей (86) f(t), получим

.

Разделим обе части на t, и перейдем к пределу поt:

.

Если пределы существуют, то полагая

,

будем иметь

, где.

Решая это уравнение, получаем выражение

.

Подставляя его в (84), получим

или

. (88)

Дифференцируя (88), получаем требуемое

._▼(89)

Определим

.

Учитывая условие отсутствия последействия, можем воспользоваться сверткой

,k  N. (90)

Используя (89), имеем

. (91)

Из смысла и (90), приk= 0, получаем

. (92)

Дифференцируя (91) по t, приходим к системе уравнений

,. (93)

Система рекуррентных линейных дифференциальных уравнений (93) легко решается, начиная с k = 1, если учесть (92) и начальные условия:V_к(0) = 0,kN. Решение системы (93) имеет вид:

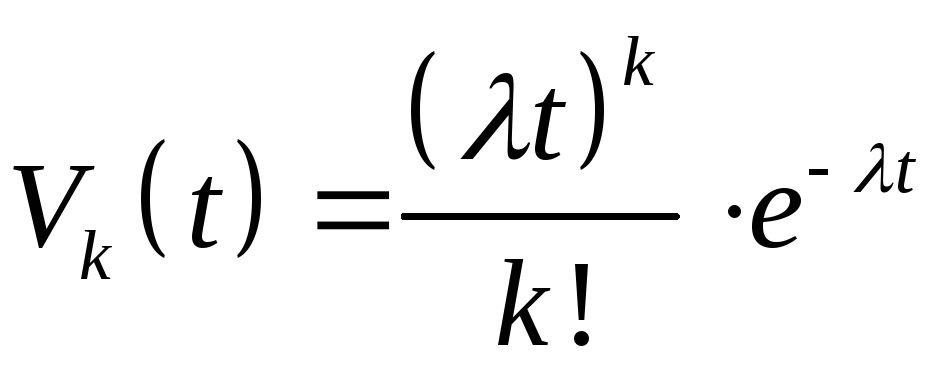,k= 0, 1, 2, ... . (94)

Формула (94) представляет пуассоновскийпроцесс (иличисто случайный процесс) с дискретным пространством состояний и непрерывным временем.

Система уравнений (93) называется системой уравнений чистого рождения[6].

Вывод. Если в некоторой системеSпереходы ее из одного состояния в любое другое удовлетворяют условиям простейшего потока, то говорят, что имеет место пуассоновский процесс с непрерывным временем. Обратное также справедливо.

Пуассоновский процесс обладает некоторыми замечательными свойствами, используя которые легко получать системы уравнений вида (93), часто применяемые в системах массового обслуживания.