2. Моменты

Пусть случайная величина имеет математическое ожиданиеМ=а. Введем новую случайную величину=-а. Случайная величинаназываетсяотклонением случайной величины.

Математическое ожидание отклонения равно 0.

В самом деле, имеем

М =М (-а) =М-Ма=а–а= 0 ._▼

Геометрически это означает, что среднее значение отклонения всегда находится в начале координат.

Определение.Начальныммоментом_кпорядкакслучайной величины называется математическое ожидание случайной величины^к:,кN, и вычисляется по формуле:

а) ,iN, если- дискретная; (32)

б) , если- непрерывная. (33)

Начальные моменты порядка ксуществуют, если их правые части в (32) и (33) имеют смысл.

Математическое ожидание есть начальный момент первого порядка М=₁.

Определение.Центральныммоментом_кпорядкак, случайной величины, называется математическое ожиданиек-ой степени отклонения

_к =М (-М)^к,к.

и вычисляется по формуле:

а) ,iN, если- дискретная; (34)

б) 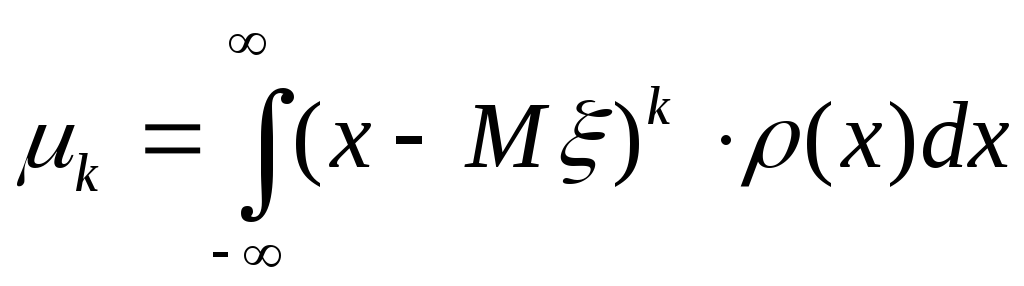, если- непрерывная. (35)

Очевидно, что если существует момент порядка к, то существуют все моменты низшего порядка.

Определение.Дисперсиейслучайной величиныназывается центральный момент второго порядка. Дисперсия обозначается символомD:

D=M (-M)² . (36)

Дисперсия число неотрицательное, и характеризует средние отклонения случайной величины от ее среднего значения.

Свойства дисперсии

Пусть - случайные величины иR, тогда

1) дисперсия постоянной равна 0, то есть D= 0.

В самом деле, при 

D=M()²=M(²=M0 = 0._▼

2) для любой случайной величины иR

D()=² D.

В самом деле,

D()=М(())² =М((-М))²=М² ()²) =² М)²= =² D._▼

3) если инезависимы, то

D() =D+D.

В самом деле, имеем:

D(М(² =² ^ +^ ()D +D=DD,

так как из независимости иследует независимость их отклонений._▼

Часто вместо формулы (36) используют эквивалентную ей формулу

D=(²) – (². (37)

В самом деле,

D=М ^^ ^^^^^._▼

Для практических приложений более удобной характеристикой случайной величины является среднеквадратичное(стандартное) отклонение, вычисляемое по формуле:

. (38)

Среднеквадратичное отклонение имеет ту же размерность, что и сама случайная величина, а дисперсия - квадратичную. Основной недостаток стандартного отклонения, в отличие от дисперсии, в том, что оно не обладает свойством аддитивности. Это означает, что, если для независимых случайных величин и

D(+) =D+D,

то для стандартного отклонения

.

Математическое ожидание и дисперсия наиболее популярные числовые характеристики случайных величин, поскольку они отражают наиболее важные свойства распределения. Для детального изучения случайных величин применяются моменты высших порядков. Мы рассмотрим здесь коэффициент асимметриииэксцесс.

Определение.Асимметриейраспределения называется свойство кривой распределения, указывающее на отличие от симметричности распределения случайной величины.

Мерой асимметрии распределения является коэффициент асимметрииS_к, определяемый равенством

,

где ₃- третий центральный момент распределения вероятностей случайной величины.

Асимметрия положительна, если S_к, отрицательна, еслиS_ки равна нулю, если распределение симметрично.

При положительной асимметрии более «длинная» часть плотности распределения лежит правее моды и отрицательна, если левее моды.

Замечание. Для распределений симметричных относительно математического ожидания все моменты нечетного порядка, если они существуют, равны нулю.

В самом деле, например, если случайная величина имеет плотность х, то

,к= 0, 1, ...,

что сразу следует из свойств интеграла от нечетной функции с симметричными пределами.

Таким образом, любой центральный момент нечетного порядка может быть использован для характеристики асимметрии.

Определение.Коэффициентом эксцесса(эксцессом) распределения вероятности случайной величиныназывается числовая характеристикаЕ_k, определяющая «островершинность» плотности распределения, и вычисляется по формуле:

,

где ₄– четвертый центральный момент вероятностного распределения. Число 3 связано с эксцессом нормального распределения, так как для него. В силу исключительной важности нормального распределения в теории вероятностей с ним сравниваются распределения вероятностей отличных от нормального. Таким образом, для нормального распределенияЕ_k= 0. Если вершина распределения более «остра» чем нормальное, то эксцесс положителен, если более «плоска», то эксцесс отрицателен. Геометрическая интерпретация этого факта представлена на рис. 16.

Рис. 16

Рассмотренные числовые характеристики случайных величин являются наиболее употребительными на практике. Достаточно часто ими пользуются для приближенной замены одного распределения другим, более подходящим.