3.1 Закон больших чисел

Теорема (Чебышева). Для последовательности независимых случайных величин , с дисперсиями ограниченными в совокупности (то есть С ), имеет место асимптотическая оценка^*

, ,. (113)

Доказательство. Положим , тогда. Для каждого фиксированногоn, в силу (112), имеем

. (114)

Из свойств дисперсии следует, что

.

Усилив (114), получим

Переходя к пределу при n  , и, учитывая, что вероятность больше единицы не бывает, получаем требуемое. _▼

Замечание. Теорема Чебышева справедлива и для случайных величин, у которых функции распределения, вообще говоря, различны.

Из теоремы Чебышева можно получить важные частные случаи.

Теорема. (Хинчина). Дана последовательность независимых случайных величин ,… с одним и тем же распределением и ограниченной дисперсией, тогда

,

где

.

Пример. Дана последовательность независимых случайных величин ,…, заданных на вероятностном пространстве (,ℱ,Р) с функцией распределения Коши:

, i  N .

Можно ли применить к этой последовательности теорему Хинчина?

Решение. По условию теоремы Хинчина, дисперсии случайных величин ограничены. Проверим это условие. Найдем сначала математическое ожидание. Имеем

.

Так как математическое ожидание не существует, то не существует и дисперсия, следовательно, теорема Хинчина для этой последовательности неприменима по двум ее условиям.

Замечание. Для теоремы Хинчина, вообще говоря, кроме независимости случайных величин достаточно существование конечного математического ожидания [5].

Из теоремы Хинчина следует, что, если при многочисленных измерениях некоторой величины, допускаются случайные ошибки, то их среднее арифметическое дает измерение, наиболее близкое к истинному.

Теорема (Бернулли). Пусть - число появлений событияА в n независимых испытаниях, а р– вероятность появления события А в каждом испытании, тогда

0, .

Доказательство. Рассмотрим независимые случайные величины , где

тогда

Ограниченность дисперсии следует из того, что, взяв производную от выражения

получаем, что максимальное значение р = 1/2,

тогда

Все условия теоремы Чебышева выполнены. Учитывая, что получаем

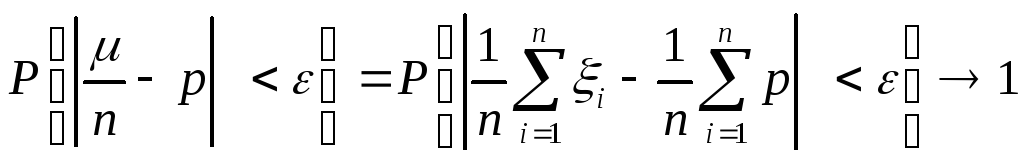0, при._▼

Теорема Бернулли утверждает, что чем больше мы будем проводить независимых испытаний, тем точнее будет оценка вероятности события А в среднем.

Теорема (Пуассона). Если для последовательности независимых испытаний вероятность появления события А в испытании к равна ,к N , то

, .

Доказательство. Достаточно заметить, что

,

то есть дисперсии ограничены в совокупности. Все остальные условия теоремы Чебышева, очевидно, выполняются. _▼

Из теоремы Пуассона следует, что, если при проведении независимых испытаний, вероятность появления события А меняется незначительно за счет случайных причин, то при достаточном числе испытаний мы получим значение близкое к истинному значению вероятности события А.

Для произвольной последовательности случайных величин закон больших чисел может быть сформулирован следующим образом.

Теорема (Маркова). Дана последовательность произвольных случайных величин ,… и для каждого фиксированногоn

, (115)

тогда

, .

Условие (115) означает, что для любого конечного n, среди случайных величин нет таких, которые существенно влияли бы на их сумму.

Закон больших чисел фактически обосновывает статистическую вероятность [4], устойчивую к ослаблениям условий ее получения, если число испытаний достаточно велико.