Свойства эмпирической функции распределения

1)

2)

3. имеет ступенчатый вид, непрерывна слева по определению,

4. если

5. если

Видно, что свойства эмпирической функции распределения вполне аналогичны теоретической.

Для оценки эмпирической функции распределения теоретической используют критерий Колмогорова А.Н.

Теорема. Если функция F(x) непрерывна, то

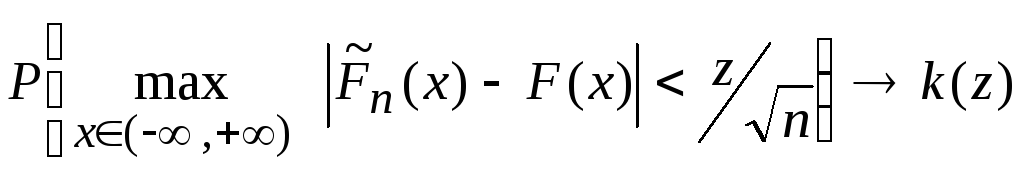при n,

где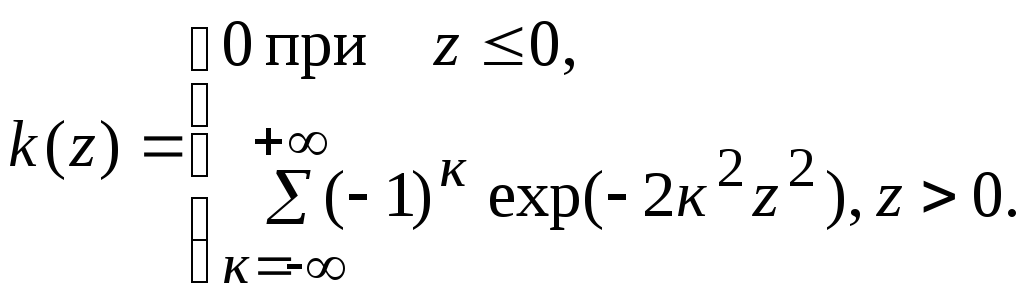

Функция называется функцией Колмогорова 2. Её значения табулированы и приведены в приложении (табл. 5).

Замечание. Из теоремы следует, что критерий Колмогорова применим для оценки только непрерывных распределений.

Пусть требуется проверить гипотезу Н_о о том, что случайная величина  имеет своей функцией распределения непрерывную функцию F(x). Проведем n независимых испытаний и построим эмпирическую функцию Согласно теореме Гливенко [2] есть приближение к функции .

Величина есть мера отклонения Пусть такое, что , где . Если можно считать, что в единичном испытании практически невозможно произойти событию, вероятность которого равна , то мы приходим к следующему критерию проверки гипотезы Н₀ (Критерий Колмогорова).

Выдвигаем гипотезу Н₀: F(x) – функция распределения исследуемой сл. в. .

1. Находим

2. Вычисляем

3. По таблице находим .

4. Если достаточно велико (больше 0,2),

то гипотезу Н₀ принимаем.

Пример 1. При концентрировании молочного сырья проницаемость растворителя через мембрану является случайной величиной , распределенной по эмпирическому закону:

.

Таблица 12

(мин)	5	10	15	20	25	30	35	40	45
	0,135	0,26	0,36	0,45	0,518	0,57	0,628	0,648	0,735

50	55	60	65	70	75	80
0,78	0,72	0,83	0,85	0,875	0,892	0,91

Требуется, используя критерий Колмогорова, подобрать теоретическую функцию распределения сл. в.  при числе опытов n = 16.

Решение. Из практических соображений есть основание считать, что искомой функцией является экспоненциальное распределение:

,

Составим таблицу значений теоретической функции распределения.

 (мин)	5	10	15	20	25	30	35	40	45
10-3F()	139	259	362	451	528	593	650	700	741

50	55	60	65	70	75	80
777	808	835	858	878	895	909

Максимальный разброс D_n при  = 55 мин. равен: , тогда . По табл. 5 приложения находим, при значение Так как ₀  1  ,2, то гипотезу об экспоненциальности распределения проницаемости принимаем.

Рис. 33 демонстрирует приближение эмпирической функции экспоненциальной.

Рис. 33

Критерий Колмогорова обладает наглядностью и простотой, однако, для его применения необходимо знать не только вид теоретической функции распределения, но и значения всех, входящих в неё, параметров. Заметим, что такая ситуация редко встречается на практике.

Другим критерием проверки гипотезы, о соответствии эмпирической функции распределения теоретической, является критерий ² (Пирсона).

Пусть имеем табл. 11. Требуется проверить согласование экспериментальных данных с гипотсзой о том, что случайная величина  имеет теоретическое распределение F(x).

Находим теоретические вероятности попадания случайной величины в каждый интервал табл. 11:

р₁, р₂, …, р_к.

Меру расхождения ² вычисляем по формуле Пирсона 3:

.

Распределение ² зависит от объема выборки n и числа степеней свободы r:

.

Во всех случаях имеем одно ограничение: значит, число степеней свободы Если в теоретическом распределении присутствует один параметр (например ), то число степеней свободы Если два параметра, (например, ), то число степеней свободы и. т. д.

Зададим доверительную вероятность р. Гипотеза о законе распределенияF(x) принимается, на уровне значимостир, если

.

При использовании критерия ² желательно, чтобы объем выборки был достаточно велик (n>50), а число интервалов к  5.

Пример 2. Для проверки соответствия опытных данных экспоненциальному распределению примера 1, применим критерий ². Объем выборки n = 16, число степеней свободы r = 16-2 = 14. Будем считать, что число интервалов к = 16.

Взяв середину интервалов из табл. 12, получим следующую таблицу:

Таблица 13

i		2,5		7,5		12,5		17,5		22,5		27,5		32,5
		0,135		0,125		0,1		0,09		0,068		0,082		0,048
iрi		0,338		0,938		1,250		1,575		1,530		2,255		1,560
37,5	42,5		47,5		52,5		57,5		62,5		67,5		72,5		77,5
0,052	0,04		0,04		0,03		0,02		0,02		0,025		0,017		0,018
1,950	1,700		1,900		1,575		1,150		1,250		1,688		1,233		1,395

Из табл. 13 находим: .

Для теоретической функции распределения , гдезначения вероятностейр_i найдем из формулы:

или

Результат сведем в таблицу:

	2,5	7,5	17,5	22,5	27,5	32,5
pi	0,193	0,349	0,576	0,658	0,724	0,778
	0,0174	0,00536	0,0012	0,0024	0,0034	0,00067

37,5	42,5	47,5	52,5	57,5	62,5	67,5	72,5	77,5
0,821	0,855	0,884	0,906	0,924	0,949	0,951	0,960	0,968
0,019	0,001	0,0051	0,0024	0,00022	0,0017	0,0014	0,00071	0,00125

Составим сумму

= 16  0,0829 = 1,326.

Зададим доверительную вероятность р=0,95.

По таблицам приложения (табл. 6), при n - r = 16 – 2 = 14 степеней свободы, определяем значение ² = 23,7,а так как , то с вероятностью р = 0,95 гипотеза, о соответствии эмпирической функции теоретической, принимается.

Упражнение. Решить пример для случая, когда число интервалов к = 8.

Замечание. В предлагаемых примерах соответствие настолько хорошее, что вызывает сомнение в том, что эмпирические данные не подтасованы. В практических приложениях уже при   0,3 гипотезу можно считать правдоподобной, тем более, если критерий Колмогорова дает аналогичный результат.

Замечание. Следует заметить, что для критерия Колмогорова параметр 0,03 взят интуитивно, а для критерия ², он получен по опытным данным. Если бы мы для поверки гипотезы использовали бы   0,03 в критерии ², то соответствие было бы еще лучше. Следовательно, можно поставить задачу о нахождении интервала допустимых значений параметра , которая рассматривается ниже.

Как видно, для применения критерия Пирсона, необходимо иметь достаточно большой объем выборки, да и его использование, по сравнению с критерием Колмогорова, достаточно громоздко. Тем не менее, применение критерия Пирсона обладает тем преимуществом, что числовые значения параметров теоретической функции распределения можно получить из имеющейся выборки, то есть заранее нам достаточно знать только общий вид теоретической функции распределения, причем любой случайной величины. Критерий Колмогорова в этом смысле более жесткий. Желательно при проверке гипотезы о соответствии теоретической функции распределения эмпирическим данным, применять оба критерия.

Задача нахождения теоретической функции распределения требует проведения достаточно большого числа опытов, а также, по крайней мере, общего вида искомой функции. Такая ситуация далеко не всегда встречается на практике.

Чаще всего имеется выборка относительно малого объема или вид теоретической функции распределения неизвестен.

В этом случае обычно вычисляют числовые характеристики случайных величин (моменты, вероятности и т. д.).