2.1 Числовые характеристики случайных величин

Случайная величина полностью определяется своей функцией распределения (или плотностью, если она существует). Однако, чтобы эту функцию найти, требуется иметь не только большой объем статистических данных, но и быть уверенным в том, что они отражают все существенные свойства случайной величины. К сожалению, это бывает редко, а во многих случаях в этом нет необходимости. Достаточно бывает проанализировать часть свойств случайной величины.

Рассмотрим некоторые типичные плотности, и определим по ним числовые характеристики, знание которых поможет получить информацию о случайной величине, без знания вида самой плотности.

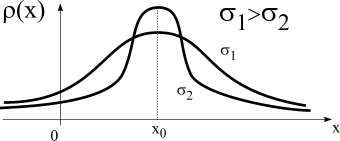
Рис. 13

Из графиков плотностей (рис. 13, 14) видно, что желательно знать абсциссу центра тяжести х₀, сгруппированность большей части площади около центра₁,₂, асимметричность₃, крутость₄, число максимумовх₁,х₂, вероятность максимального значения плотностих₀(рис.13),х₁, и другие.

Рис. 14

Знание хотя бы части этих характеристик позволяет достичь желаемой цели без знания плотности. Наконец, при исследовании какой-либо проблемы, мы начинаем ее изучение с общих позиций, оцениваем ее в среднем. Именно для изучения этих сторон, в первую очередь, и предназначены числовые характеристики случайных величин. Мы рассмотрим здесь лишь некоторые из них.

2.1.1 Математическое ожидание, мода, медиана

Пусть имеем произвольное вероятностное пространство (ℱ,Р), на котором определена случайная величина.

Определение.Математическим ожиданиемилисредним значениемслучайной величиныназывается числоМ, которое находится по формуле:

а) если случайная величина дискретна, то есть задана табл. 2,

Таблица 2

	x1	x2	…	xn	…
p	p1	p2	…	pn	…	(pi=1),	iN,

то

, (30)

и существует, при условии, что ряд в правой части (30) сходится;

б) если случайная величина непрерывна с плотностью(х), то

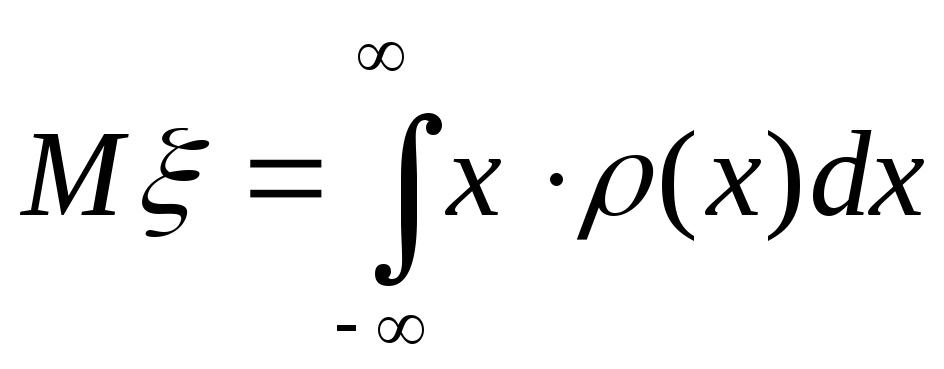, (31)

и существует, при условии, что несобственный интеграл в правой части (31) сходится.

Математическое ожидание аналогично понятию средне-взвешенного и интерпретируется как абсцисса центра тяжести распределения массы на прямой.

Свойства.

1. Если =а –const, тоМа=а.

В самом деле, рассматривая акак дискретную случайную величину с законом распределения

Ра=1,Р а,

получаем по формуле (30):

М = 0Ра+аРа=а1=а._▼

2. Постоянную можно выносить за знак математического ожидания

М(а)=аМ.

В самом деле, если , например, непрерывная случайная величина, то

._▼

3. Для любых случайных величин ,

М(+) =М+М

4. Если случайные величины , независимы, то

М() =ММ.

В самом деле, если случайные величины независимы, то их совместная плотность, равна произведению плотностей случайных величин^*, то есть

_ (х,у) =_(х)_ (у),

тогда

= ММ._▼

5. Всегда .

В самом деле, имеем

. _▼

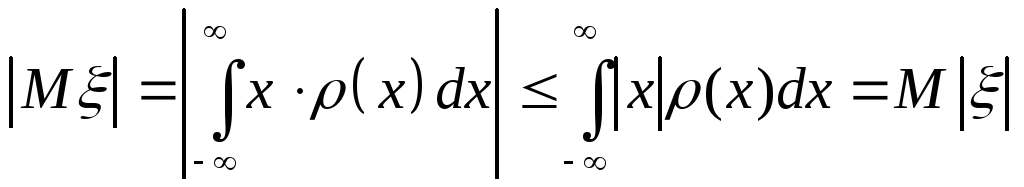Пример. Найти математическое ожидание индикатора событияА .

Решение. По определениюI()=I_A() =, тогда для любого

М(I()) =Р()1(1Р()).

Так как , тоМI(А)) =М(.

Таким образом, вероятность события А можно записать через математическое ожидание индикатора событияА.

Математическое ожидание случайной величины является важнейшей, среди ее «линейных характеристик». На практике, в качестве характеристик, дополняющих математическое ожидание, используютмодуимедиану [3].

Определение.МодойМ₀дискретной случайной величиныназывается ее наивероятнейшее значениек₀.

Модой непрерывной случайной величины называется любое из значенийх, в котором плотность имеет максимум.

Графическая интерпретация моды приведена на рис. 14.

Определение.Медианойнепрерывной случайной величиныназывается ее значениеМ_е, для которого

РМ_еРМ_е.

Рис. 15

На рис. 15 изображена плотность вероятности, где медиана есть абсцисса М_е =х, для которой

Можно определить медиану и для дискретной случайной величины, например, как среднее арифметическое наименьшего и наибольшего ее значений [1], однако обычно медиана используется при изучении непрерывных случайных величин.