2.3.4 Моменты многомерных случайных величин

Определим, по аналогии, начальные и центральные моменты системы двух случайных величин в предположении существования их ряда распределения (или плотности).

Определение.Начальныммоментом порядка (к +r) системы случайных величин (,) называется число

	если (,) - дискретная
	если (,) - непрерывная

В частности, _1,0 =, _0,1=,n N.

Определение.Центральным моментом порядка (к+r) системы случайных величин () называется число

, (57)

в частности ,.

Выясним что представляют собой начальный момент _1,1и центральный момент_1,1системы (.

Рассмотрим более общую задачу. Пусть ₁,₂, …,_n- произвольные случайные величины. Вычислим дисперсию их суммы:

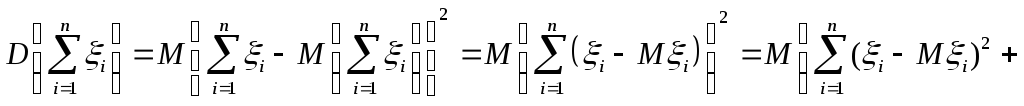
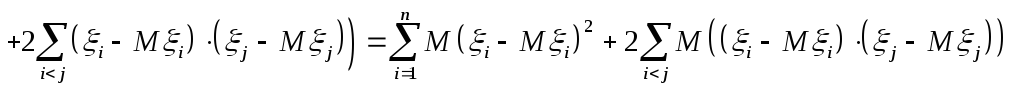или

. (58)

Число слагаемых во второй сумме, правой части (58), равно

Если бы случайные величины были независимы, то, в силу свойств математического ожидания,

,.

Число , в формуле (58), является вторым смешанным центральным моментом_1,1пары случайных величин_i,_j.

Его можно рассматривать как меру зависимости случайных величин.

Определение.Ковариациейслучайных величин,называется математическое ожидание произведения их отклонений

. (59)

Ковариация существует, если существуют дисперсии каждой из случайных величин. Очевидно, что дисперсия есть частный случай ковариации, так как при имеем .

Если случайные величины независимы, то ковариация равна 0. Утверждение сразу следует из свойств математического ожидания отклонений этих величин. Обратное неверно.

Вместо формулы (59) часто используется формула

. (60)

В самом деле, имеем

._▼

Пример. (Игра в лотерею). У каждого играющего в лотерею свой номер. Карточки с номерами собирают и тщательно тусуют. Затем по очереди, в соответствие с номером, игроки подходят и берут карточки. Получает приз тот, кто взял свой номер. Оценить, сколько призов в среднем следует приготовить.

Решение. Определим сл. в._к =

А_к ~игрок с номеромквытащил карточку с номеромк. Пусть- случайная величина, характеризующая число призеров. Ясно, что свою карточку игрок берет с вероятностьюn^-1:

,,,

но тогда

,

то есть, имеем одно совпадение при любом n.

Найдем дисперсию:

,,

,

.

Из определения следует, чтоможет быть равно 1 или 0, причем, если обе карты на своем месте, то есть,.

Итак, , а так как число слагаемых у второй суммы есть, то

.

Таким образом, с учетом средних отклонений, получается, что независимо от числа игроков следует приготовить приза в среднем.

Пример. Пусть случайная величинараспределена равномерно в кругеDрадиусаR (для простоты центр круга поместим в начало координат). Определим плотность

Вычислим В силу симметрии,,. Далее,

,

то есть некоррелированы, хотя и зависимы. В самом деле, имеем

, ,

тогда

.

Задача. Доказать, что для нормального распределения случайных величиниз некоррелированности вытекает их независимость.

Из примера видно, что величина ковариации зависит от размерности случайных величин . Целесообразно ввести безразмерную характеристику, которая будет являться мерой зависимости случайных величин.

Определение. Случайная величина* называетсянормированной, еслиМ* =0,D*= 1. Любую случайную величинуможно нормировать заменой

.

Определение.Коэффициентом корреляцииrслучайных величин, входящих в двумерную случайную величину, назовем нормированную ковариацию:

.

Если r= 0, то говорят, что случайные величинынекоррелированы. Независимые случайные величины всегда некоррелированы.

Если рассматривать геометрический образ случайных величин в декартовых координатах, то для их некоррелированности достаточно, чтобы их совместное распределение было симметрично относительно прямой параллельной любой из осей координат.