Свойства плотности

Свойство 1.. (23)

Доказательство. Проверим свойства 1)-5) функции распределения.

Пусть (х) - плотность, тогда(х), отсюда

1. (х₁ х₂)

2. непрерывность слева следует либо из непрерывности (х), либо из ее кусочной непрерывности с разрывами первого рода;

3. следует из существования интеграла на действительной оси;

4. F(-) =;

5. F(+) = 1, из определения.

Свойство 2.. (24)

Для доказательства достаточно продифференцировать (23) по переменному верхнему пределу._▼

Учитывая (23) и (24), функцию распределения называют интегральной, а плотностьдифференциальнойхарактеристикой случайной величины.

Плотность имеет смысл для такой случайной величины, функция распределения которой дифференцируема; обычно, это непрерывная случайная величина. Функция распределения - это вероятность, и по определению безразмерна. Для плотности, как следует из формулы (24), размерность обратна размерности случайной величины. Физически, плотность характеризует мгновенное изменение случайной величины в точке х.

Для дискретной случайной величины понятие плотности лишено смысла, поскольку, как видно из примера для индикатора, она либо равно нулю, либо имеет бесконечное изменение в точке разрыва.

Отметим некоторые полезные свойства функции распределения и плотности:

1) ,

2) ,

3. Рхх+dx =  (х)dx,

4. Р=а= F (a+0) – F(a-0),

5. Ра = F (a +0 ).

Упражнение. Доказать свойства 1 – 5.

Примеры основных распределений

Пример 1. Пусть случайная величинаесть число появлений событияАвnнезависимых испытаниях (вероятность появления события А в любом испытании равнар). Построить функцию распределения.

Решение.Рассмотрим событиех~,хR.

По условию, если , то полагаем,F(x)=0 длях0. , для 0х n, иF(x) = 1, дляхn. Таким образом,

(25)

График функции имеет ступенчатый вид (рис.7):

Рис. 7

Из графика видно, что свойства 1) – 5) выполняются. Величину скачка функции в точке х=kнаходим из равенства

.

Пример 2. Будем говорить, что случайная величинаимеет распределение Пуассона, если ее функция распределения имеет вид:

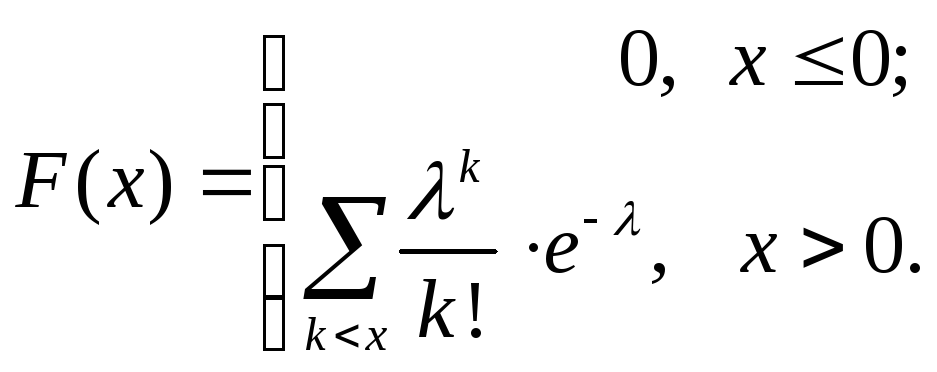(26)

Свойства 1)- 4) очевидны. Проверим 5):

.

Рис. 8

Величина скачка в точке х=kравна,. Число разрывов счетно. График функции представлен на рис. 8.

Пример 3. Будем говорить, что случайная величинаравномерно распределена на (а,в], если ее функция распределения имеет вид:

(27)

Плотность равномерного распределения

(28)

Рис. 9

Из графиков (рис.9) видно, что значение есть площадь (интеграл) области, ограниченной справа прямойх =х₀.

Пример 4. Случайная величинараспределена нормально, если ее функция распределения имеет вид:

,

а плотность

,>0,a–const.

Свойства функции распределения 1 - 4 очевидны. Проверим свойство 5.

=интеграл Пуассонаℑ = =.

Схематично график плотности (рис. 10) имеет вид:

Рис. 10

Постоянная ахарактеризует сдвиг функции(x) по оси ОХ относительно начала координат, а- меру «сжатости» кривой около центра в точкех=а .

Пример 5. Случайная величинаимеет показательное (экспоненциальное) распределение, если ее функция распределения определяется по формулой

(29)

Если х– интерпретировать как время, то функция распределения будет иметь вид (рис. 11):

Рис. 11

Это распределение играет важную роль в технике и носит название функции надежности, - интенсивность с размерностью обратной времени [1].

Плотность , ее график функции имеет вид (рис. 12):

Рис. 12