Окончательно

2,9528<M<3,1108;

б) для D, при  = 1-  ,0.

Из формулы (138) и приложения, таблица 7, для р= и r = 21, имеем .

Тогда для D , из формулы (138), получаем

или .

Сравнивая результаты для приближенного и точного методов интервальных оценок, можно выдвинуть гипотезу о том, что если доверительный интервал для математического ожидания меняет центр симметрии, то для дисперсии он тем больше, чем ближе к нормальному распределению выборка.

4.4 Проверка статистической однородности

Теория вероятностей изучает такие события, результат которых устойчив, или, что тоже самое, статистически однороден. Как определить, достигли мы желаемого результата, после проведенной серии экспериментов, или нет? Следует ли провести еще одну серию, чтобы закрепить свои предположения? Ясно, что исчерпывающего ответа на эти вопросы получить нельзя.

Однако некоторые оценки сделать можно, если использовать центральную предельную теорему.

Пусть имеем случайную величину  =  (₁, …, _n), с нормированным нормальным распределением (М = 0, D = 1), где ₁, ..., _n – результат серии экспериментов.

Поставим задачу. Проведено две серии экспериментов: в первой серии из n₁ экспериментов событие А появилось ₁ раз, а во второй серии из n₂ экспериментов событие А появилось ₂ раз. Можно ли предполагать что вероятность события А одинакова в обоих случаях?

Пусть в первой серии Р{А}= р₁, а во второй Р{А}= р₂. Верна ли гипотеза Н₀: р₁ = р₂?

Для ответа на вопрос, необходимо чтобы разность частот , была достаточно мала, тогда ее можно объяснить случайными причинами. Если ошибка в самом деле мала, то естественно предположить, что случайные величины ₁ и ₂ распределены нормально, то есть при р₁ = р₂, будем иметь .

Если считать, что серии опытов независимы, то  имеет распределение близкое к нормальному, у которого и

Если значение известно, то по табл. 3 приложения, нормального распределения, можно получить ответ на вопрос.

Серии опытов, в силу предположения, будем считать сериями испытаний Бернулли, тогда если р₁ = р₂ = р, то

.

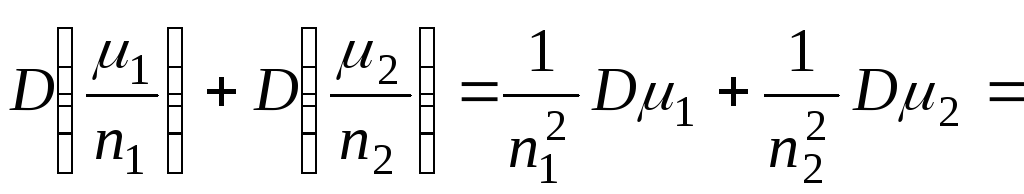
Значение р неизвестно, но используя данные эксперимента, можно заменить р на

(так как это лучшее, что можно предложить в данной ситуации), тогда

. (139)

Случайная величина  нормирована и имеет приблизительно нормальное распределение, из которого следует, что значения >2 3 маловероятны.

В самом деле, например, для = - 1,96, по табл. 3 приложения находим Ф(-1,96) = 0,0250, а для  = 1,96, значение Ф ( >1,96) = 0,0250 (рис. 35).

Рис. 35

Представим сказанное на языке теории вероятностей, то есть определим область принятия гипотезы Н₀.

Заранее зададим малое  (например,  = 0,05), означающее, что событию с такой вероятностью произойти практически невозможно. Число  называется уровнем значимости. Используются значения 0,1; 0,05; 0,02; 0,01; 0,001.

Пусть значение случайной величины , в данной серии испытаний, оказалось равным  =. Если   0, то находим Р = Ф; Если  >0, то имеем Р > = 1-Ф+  (табл. 3 приложения).

Объединяя, значения вероятностей, получаем Р  > = 2Ф- (в нашем случае, Р  >=20,025 = 0,05, рис. 35). При 2Ф-  , гипотеза Н₀ отвергается, иначе – данные выборки не противоречат гипотезе Н₀ и ее нет оснований не принять, если отсутствует субъективный фактор.

Замечание. Так как, например, как в нашем случае, при Ф = 0,0250 следует, что  = -1,96, то область принятия гипотезы Н₀ есть -1,96    1,96.

Если значение вероятности равно или близко к , то принять гипотезу Н₀ или отвергнуть, зависит от изучаемого объекта и субъективного фактора.

Задача. Пусть вероятность успеха р, заданной серии n испытаний Бернулли предполагается равной числу р₀ . Если проверяется гипотеза Н₀: р = р₀, то случайная величина

(140)

(где  - число успехов в серии)

имеет, приблизительно, стандартное нормальное распределение.

Вывод формулы (140) вполне аналогичен предыдущим рассуждениям.

Пример. Проверяется симметричность монеты, гипотеза Н₀: р₀ = 0,5, по двум проведенным сериям из n испытаний Бернулли каждая, для уровня значимости  = 0,05.

Герб имеет частоту а) в первой серии , б) во второй серии . Требуется проверить однородность выборок и выполнение гипотезы Н₀ для первой, второй и обеих серий.

Решение. Проверим выборки на однородность. Имеем, по формуле (139),

.

Так как -0,447>-1,96 (см. замечание), то гипотеза Н₀ принимается, то есть с вероятностью 0,95 можно считать, что монета симметрична.

Проверим монету на симметричность по первой выборке. По формуле (140) имеем

.

Так как –1,26 >-1,96, то гипотезу Н₀ принимаем. Для других вариантов результат, очевидно, будет лучше.