2.3.5.1 Марковские процессы

Понятие марковкой цепи принадлежит русскому математику А.А. Маркову (в статьях 1906-1908 гг., где он использовал новое понятие для статистического анализа распределения букв в поэме А.С. Пушкина «Евгений Онегин»). Само понятие «Цепь Маркова» было предложено русским математиком А.Я. Хинчиным.

Пусть имеем некоторую систему S, которая может находиться в одном из конечного или счетного множества несовместных состоянийС_i,i N. Переход системы от состояния к состоянию, вообще говоря, случаен и возможен только в фиксированные моменты времениt_n,n= 0,1,2,… . Опишем функционирование системы в терминах случайных процессов.

Пусть в момент времени t_n, системаSперешла из состоянияС_jв состояниеС_i. Для ее описания зададим дискретный случайный процесс функциейt_n) = _i,t_n),i= 1, 2, …;n= 0, 1, … . Элементарное событие_iотражает пребывание системыSв состоянииC_i. Кроме того, нам необходимо задать начальное распределение вероятностей для момента времениt=t₀и, в общем случае, задать все сечения процесса и возможность его реализации.

Получить такую информацию о случайном процессе задача трудновыполнимая, да и в ряде случаев не нужная, если использовать понятие цепей Маркова.

В самом деле, пусть имеем последовательность (цепь) зависимых целочисленных случайных величин _n=t_n),n= 0,1,… . Если в моментt_nсистема пришла в состояниеC_i, то будем считать, что_n=i.

Определение. Последовательность случайных величин {_n},n= 0,1,… образуетцепь Маркова, если

,(66)

с начальными условиями

,. (67)

Вероятности - называются вероятностями перехода. Свойство (66), цепи Маркова, называетсясвойством отсутствия последействия, которое интерпретируется так:поведение процесса в будущем зависит только от фиксированного настоящего и не зависит от его прошлого.

Определение. Цепь Маркова {_n},n= 0, 1, …, называетсяоднородной, если вероятности переходане зависят от времени, то есть

,. (68)

Определение. Цепь Маркова называетсянеприводимой, если каждое ее состояние может быть достигнуто из любого другого, то есть для любых двух состояний системыSС_i,C_j, существует целое числок, такое, что.

Для однородной цепи имеем .

Пусть - вероятность того, что в момент времениt_nсистема находится в состоянииС_j. Интерес представляет существование предела

,. (69)

Нахождение распределения {_j} является основной задачей цепей Маркова. Если предел существует, то говорят, что системаSимеетстационарныйрежим функционирования, если. Предельные вероятности {_j} не зависят от начальных условий,,, означают долю времени, в течение которого система находится в состоянииС_j,jN, и однозначно определяются равенствами:

, (70)

,. (71)

Формула (70) называется условием нормировки.

Система алгебраических уравнений (71) является однородной, и для ее однозначного решения необходимо использовать (70), при этом, любое одно уравнение из системы (71) можно исключить.

Матрица П, составленная из элементов, называется матрицей вероятностей перехода:

. (72)

Зададим вектор вероятностей состояний системы

.

тогда система (71) записывается в виде

. (73)

Часто представляют интерес переходы системы из состояния в состояние в произвольный момент времени (переходный режим).

Для этого нужно определить распределение вероятностей пребывания системы в состоянииС_j в моментt_n. Зададим вектор вероятностейв моментt_nравенством

.

Используя (71) и определение вероятностей переходов (66), имеем

,

где - начальное состояние системы (67). Отсюда для любогоn, по рекуррентной формуле, получаем

,. (74)

Уравнение (74) дает общий метод вычисления вероятностей на n-м шаге процесса по заданной матрице переходовПи начальном распределении

Если стационарный режим существует, то

. (75)

Пример. Рассмотрим системуS, которая находится, в любой момент времениt, в одном из трех состоянийС₁,С₂,С₃. Переход системы от состояния к состоянию происходит мгновенно в фиксированные моменты времениt_к =к,кN, в соответствии с размеченным графом [3] состояний рисунка 28.

Рис. 28

Требуется оценить скорость сходимости к стационарному режиму и вычислить стационарное распределение вероятностей.

Решение. Вычислим стационарное распределение вероятностей, то есть найдем собственный вектор, где,i=1, 2, 3.

Имеем , где

.

С учетом условия нормировки имеем систему

(*)

Решая ее (например, без уравнения помеченного (*)), получаем стационарное распределение вероятностей:

.

Оценим скорость сходимости. Для этого вычислим вероятности перехода по формуле (74) при различных начальных условиях:

а) р⁽⁰⁾= (1,0,0),

результаты представлены в виде табл. 7.

Таблица 7

n	0	1	2	3	4	…
	1	0	0,250	0,178	0,203	…	0,2
	0	0,75	0,062	0,359	0,254	…	0,28
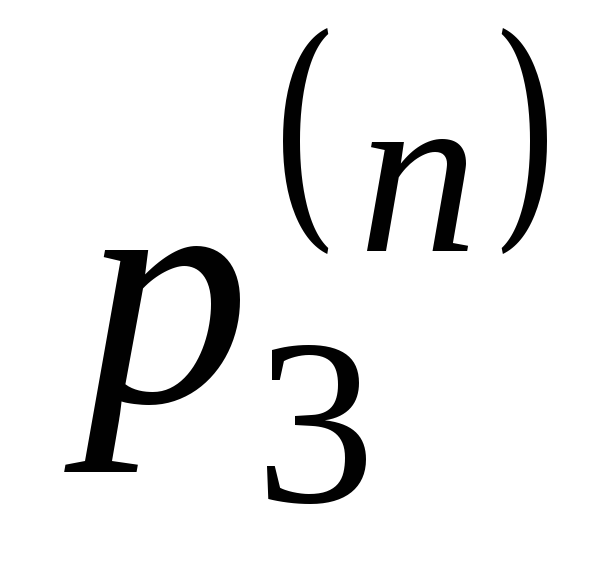
	0	0,25	0,688	0,454	0,543	…	0,52

б)р⁽⁰⁾= (0,1,0),

соответствующие результаты отражены в табл. 8.

Таблица 8

n	0	1	2	3	4	…
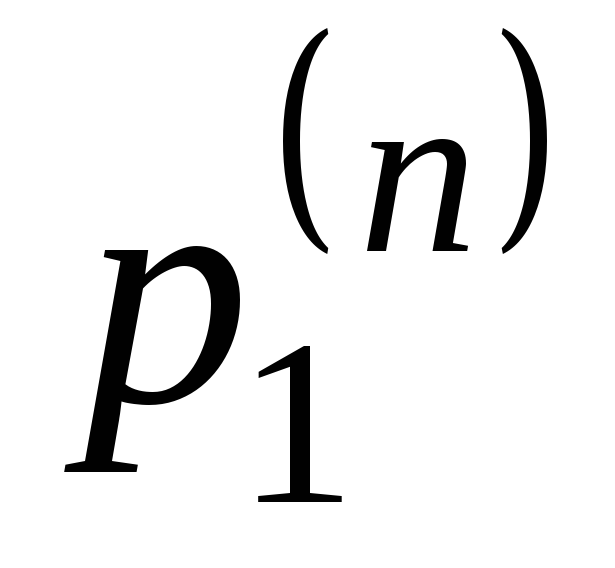
	0	0	0,187	0,203	0,199	…	0,2
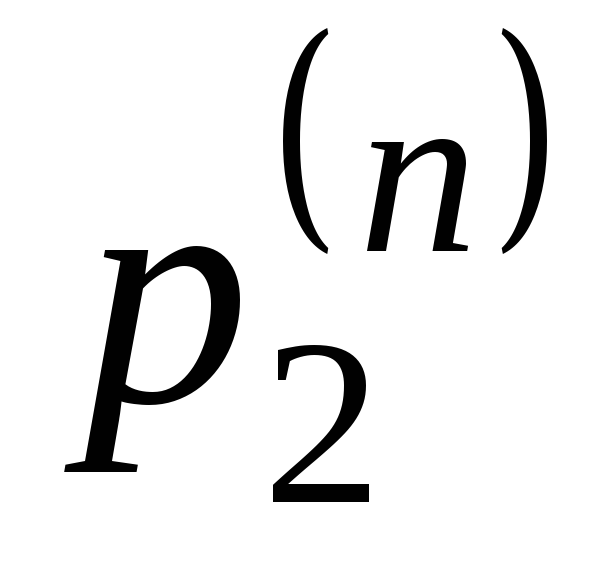
	1	0,75	0,375	0,250	0,289	…	0,28
	0	0,25	0,438	0,547	0,512	…	0,52

в) р⁽⁰⁾= (0,0,1),

в итоге получаем табл. 9:

Таблица 9

n	0	1	2	3	4	…
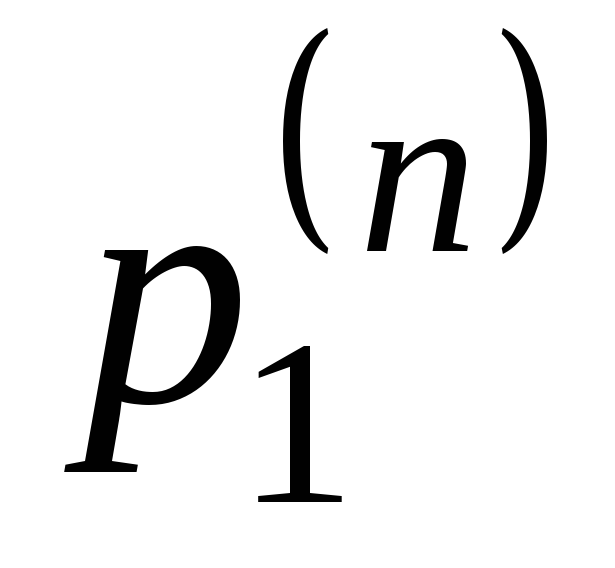
	0	0	0,187	0,203	0,199	…	0,2
	0	0,75	0,313	0,266	0,285	…	0,28
	1	0,25	0,500	0,531	0,516	…	0,52

Из таблиц видно, что вхождение системы в стационарный режим происходит достаточно быстро, так как, уже после четырех шагов, вероятности мало отличаются от предельных, независимо от начальных условий.

Замечание. Оценка скорости сходимости переходных вероятностей к стационарным зависит отсобственных значений матрицы П и иллюстрируетсябарицентрической системой координат[8].