Значения поправочного коэффициента j (t)

t	1	2	3	4	5	6	7	8	9	10	11	12
j (t)	1,000	0,539	0,381	0,304	0,262	0,244	0,210	0,194	0,182	0,174	0,166	0,160

t	13	14	15	16	17	18	19	20	21	22	23	24
j (t)	0,156	0,152	0,149	0,146	0,144	0,142	0,140	0,139	0,138	0,137	0,136	0,135

Кроме того, в литературе [1, 10] встречаются и другие методики для расчёта интегрального показателя.

При сроке службы продукции до одного года интегральный показатель I₁ вычисляют по формуле

. (3)

Наряду с интегральным показателем качества продукции может применять­ся величина, обратная ему, и называемая удельными затратами на единицу эф­фекта

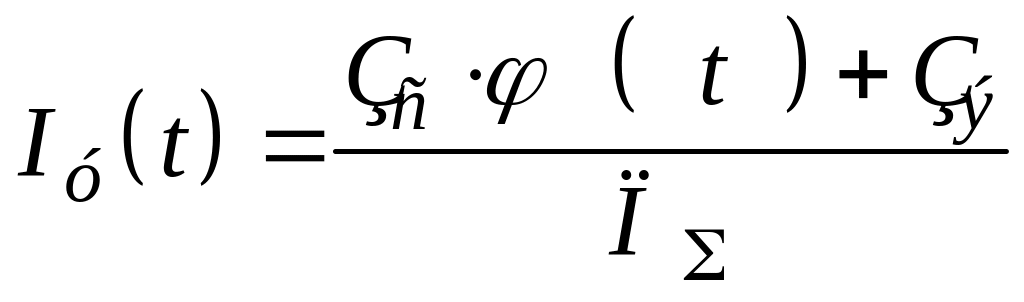. (4)

1.2.4. Виды средневзвешенных величин

Третий рекомендуемый нормативной документацией показатель, который может использоваться для комплексной оценки качества – это средневзвешенный показатель. Этот вид показателя является частным, но, безусловно, наиболее часто встречающимся на практике случаем нахождения комплексного показателя с помощью «функции свертки». «Функция свертки» – это некоторая заданная функция коэффициентов весомости М₁, М₂, . . . , М_n и оце­нок единичных показателей Q₁, Q₂, . . . , Q_n, которая используется в качестве обобщенного показателя:

(5)

Наиболее сложной проблемой при построении комплексного показателя качества является выбор и обос­нование вида этой зависимости.

В качестве «функции свертки» могут использоваться:

– средневзвешенные величины; в нормативной документации рекомендовано средневзвешенное арифметическое и геометрическое применение. Но существует еще и ряд других средних: средняя гармоническая, средняя квадратическая, средняя куби­ческая (и даже медиана), которые также принципиально могут быть использованы для этой цели;

– модификации методов средневзвешенных величин и их комбинаций;

– для свертки показателей Q_i в комп­лексный показатель качества К_k применяются различные полиномы, не являющиеся средними величинами.

В подавляющем большинстве случаев весомости отдельных свойств входят в расчётную формулу определения комплексной оценки. Однако на заре квалиметрии разрабатывались методики в которых пытались построить классификацию по­казателей свойств, при которой показатели одного уровня равноценны по весомости и, следовательно, значение их весо­мости можно не включать в расчетную формулу. Так же, как отголосок стремления избавиться от коэффициентов весомости, в пищевой промышленности при оценке уровня качества для каждого свойства назначают свою шкалу баллов. В такой методике относительная важность отдельных свойств учитывается величинами самих показателей.

Анализ различного рода методик, посвященных комплексной оценке качества продукции, свиде­тельствует о том, что выбор функциональных зависимостей для комплексных показателей качества, а также определение коэффи­циентов весомости и оценок единичных показателей во многих работах осуществляются без достаточного обоснования. Это приво­дит не только к грубым, а зачастую и неверным результатам, но и дискредитирует саму идею комплексной оценки [12].

Средние взвешенные показатели при комплексном методе оценки уровня качества продукции применяют в тех слу­чаях, когда затруднительно определение главного показателя и установление его функциональной зависимости от исходных пока­зателей качества продукции.

Из существующих 14 видов различных средних в квалиметрии используются 4, из них нормативно были закреплены средний взвешенный арифметический и геометрический показатели.

Средний взвешенный арифметический показатель вычисляют по формулам [8, 9, 14]:

; (6)

. (7)

Средний взвешенный геометрический показатель вычисляют по формулам:

; (8)

. (9)

В формулах (6)–(9):

Р_i – значение i-гo показателя качества продукции;

Q_i – относительный i-й показатель качества продукции;

m_iU – параметр весомости i-гo показателя, входящий в средний взвешенный арифметический показатель;

m_iV – параметр весомости i-гo показателя, входящий в средний взвешенный геометрический показатель;

n – число показателей качества продукции.

Параметры весомости m_iU и m_iV могут быть как размерными, например, в формуле (6), так и безразмерными, например, в формулах (7), (8), (9). Однако во всех случаях это величины положительные.

В самом общем виде комплексный показатель качества по принципу среднего взвешенного К определяют по формуле [4]:

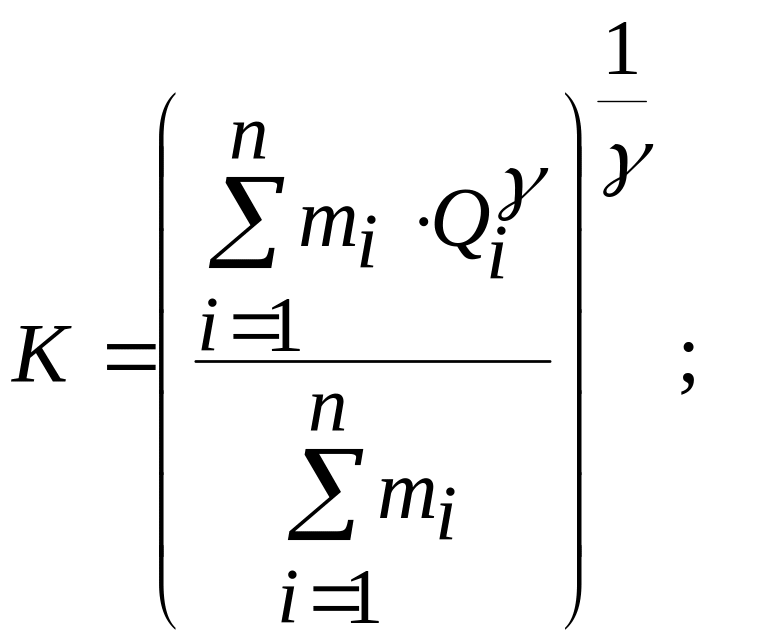⁽¹⁰⁾

где γ – параметр логики усреднения;

m_i – весовые коэффициенты показателей качества (при некоторых условиях M_i – коэффициент весомости пока­зателя качества продукции);

Q_i – оце­нки единичных показателей (при некоторых условиях P_i – единичные показатели качества );

n – число единичных показателей качества.

Задавая разные значения γ и принимая сумму весовых пока­зателей за единицу (если выполняется это условие и m_i – величины безразмерные, то в этом случае весовые коэффициенты показателей качества являются коэффициентами весомости пока­зателей качества продукции M_i), получаем различные виды средних взвешенных показателей, которые приведены в таблице 2.

Таблица 2