Дележи.

Def. Дележом называется вектор t=(t₁,…,t_n): 1) t_i ({i}) i, 2) t_i=(N).

Дележ t доминирует дележ  по коалиции S (пишем t≻_s ), если:

1) t_i>_i iS; 2)  t_i(S).

Пусть E()множество всех дележей, а R()ядро игры, т.е. множество дележей, не доминируемых никакими дележами ни по какой коалиции.

Теорема: Если игра - существенная с постоянной суммой, то R()=.

Def. Множество дележей V E() назовем НМрешением игры, если оно:

1. внутренне устойчиво, т.е. никакие два дележа из V не доминируют друг друга ни по какой коалиции;

2. внешне устойчиво, т.е. для V tV и коалиция SN: t≻_s.

НМрешение может быть не единственным или пустым при пустом ядре.

Пример К1: (продолжение) V={(1,1,2), (1,2,1), (2,1,1)};

Другое НМрешение: V={(x₁,x₁a,a)}, x₁[2,a], для a[2,1].

Вектор Шепли.

Пусть игра задана в характеристической форме (задана функция ). Относительную силу игроков характеризует вектор Шепли ()=(₁(),…,_n()):

1. () E(), т.е. является дележом;

2. сила каждого игрока не зависит от нумерации, т.е. если в игре  номер игрока= i, в игре ' его номер=k_i, то _ki(')=_i();

3. если игрок участвует одновременно в двух играх  и , то можно считать, что игра одна с характеристической функцией + и _i(+)=_i()+_i().

А ксиомы 1)3) однозначно определяют вектор Шепли:

Пример К1(прод): (0)=0=({1,2,3}); ({i})=-2; ({1,2})=({1,3})=({2,3}) =2.

В сумме для ₁() будет 4 слагаемых: коалиции {1},{1,2},{1,3},{1,2,3}. ₁=(-2-0)/(1*С₃¹)+(-2-(-2))/(2*С₃²)+(2-(-2))/(2*С₃²)+(0-)/(3*С₃³)=0, ₂=₃=0.

Недостатки вектора Шепли: а) относительная трудоемкость вычислений;

б) вектор Шепли может не принадлежать ядру, даже если ядро не пусто.

Пример К2: Пусть есть акционерное общество из 4-х акционеров. У них 23, 25, 26 и 26% акций соответственно. Выигрыш коалиции равен 1, если она об­ладает большинством акций; и 0 в противном случае. Найдем вектор Шепли.

Считаем ₁. Коалиции, где v(s) - v(s\{1})≠0: {1,2,3},{1,2,4},{1,3,4},{1,2,3,4}

₁()=(1-1)/(3*C₄³)+(1-1)/(3*C₄³) +(1-1)/(3*C₄³) +(1-1)/(4*C₄⁴)=0.

Игрок 1 является «болваном». Для остальных игроков ₂=₃=₄= ¹/₃.

Nядро (метод Шмайдлера).

Введем меру близости коалиции S и дележа t: эксцесс . Решая задачу ЛП, найдем дележи . Из них выберем дележи с наименьшим вторым по величине эксцессом и т.д. Решив несколько задач ЛП, получим единственный дележ, называемый Nядром и обладающий свойствами:

1) если игрок i болван, то t_i=0; 2) если R(), то NядроR().

Рассмотрим макроигру: два игрока независимо друг от друга выбирают коалицию и дележ, выигрыш = эксцессу. Ищем устойчивое по Нэшу решение: смесь коалиций + N-ядро. Можно решать задачу так: max l(S, t) – верхняя огибающая семейства функций. Исключим t_n и разобьем E() в ^{n -1} на области, в которых l(S, t) - линейна  решаем ЛП. Ее min на границе.

Окончание примера К1: E() ={(t₁,t₂,t₃): ∑t_i =0 & t_i v({i})=-2} ~ t₁+t₂+t₃=0 & t_i-2

S	v(S)	эксцесс		S	v(S)	эксцесс
	0	0		{1,2,3}	0	0-t1-t2-t3=0
{1}	-2	-2-t1		{2,3}	2	2-t2-t3=2+t1
{2}	-2	-2-t2		{1,3}	2	2-t1-t3=2+t2
{3}	-2	-2-t3=-2+t1+t2		{1,2}	2	2-t1-t2

Исключим в эксцессах t₃ =-t₁-t₂ -2. l̃(t)= max{0,2+t₁, 2+t₂, 2-t₁-t₂}.

Симметрия по t₁,t₂ , положим t₁=t₂=x!!

max{2+x, 2-2x}→ min

 2+x = 2-2x  3x = 0  x = 0.

N‑ядро: argmin l̃(t) = (0,0,0).

Пример К3: Одномастка на троих. Позиция - {(9,7,1),(8,4,2),(6,5,3)} с ходом 1-го игрока.

E() ={(t₁,t₂,t₃) | ∑t_i = v({1,2,3})=3 & t₁ v({1})=1 & t₂ v({2})=1 & t₃ v({3})=0}.

S	v(S)	эксцесс		S	v(S)	эксцесс
{1,2,3}	3	3-t1-t2-t3=0			0	0
{1,2}	3	3-t1-t2		{3}	0	0-t3=t1+t2-3
{1,3}	2	2-t1-t3=t2-1		{2}	1	1-t2
{2,3}	2	2-t2-t3=t1-1		{1}	1	1-t1

Исключим в эксцессах t₃ =3-t₁-t₂ 0.

l̃(t)=max{t₁-1,t₂-1,3-t₁-t₂}, t₁,t₂1 и t₁+t₂ 3 (симметрия t₁,t₂, полагаем t₁=t₂=x)

max{x-1, 3-2x}→ min

 x -1= 3-2x  3x = 4  x = ⁴/₃.

N-ядро: argmin l̃(t) = (⁴/₃, ⁴/₃, ¹/₃).

Можно решать задачу проще: точка пересечения n плоскостей в ⁿ есть точка минимума их верхней огиба­ющей. Осталось 3 плоскости. Их пересечение t = (⁴/₃,⁴/₃,¹/₃).E(). N-ядро совпало с вектором Шепли:

₁() = ₂() = (1-0)/(1∙C₃¹) + (3-1)/(2∙C₃²) + (2-0)/(2∙C₃²) + (3-2)/(3∙C₃³) = ⁴/₃,

₃() =  0/(1∙C₃¹) + (2-1)/(2∙C₃²) + (2-1)/(2∙C₃²) + (3-3)/(3∙C₃³) = ¹/₃.

???: В игре с постоянной суммой для 3-х игроков N-ядро всегда совпадает с вектором Шепли? Для четырех - не всегда.

Пример К4. На выборах 4 партии набрали 48, 32, 16 и 4 % голосов соответственно.

v-1(0)	эксцесс		v-1(1)	эксцесс
	0		1,2,3,4	1-t1-t2-t3-t4=0
1	-t1		2,3,4	1-t2-t3-t4=t1
2	-t2		1,3,4	1-t1-t3-t4=t2
3	-t3		1,2,4	1-t1-t2-t4=t3
4	-t4		1,2,3	1-t1-t2-t3=t4
2,3	-t2-t3		1,4	1-t1-t4=t2+t3
2,4	-t2-t4		1,3	1-t1-t3=t2+t4
3,4	-t3-t4		1,2	1-t1-t2=t3+t4

Как им разделить министерские портфели?

Дележ: t₁+t₂+t₃+t₄=1, t_i≥0

max _S l(S,t)= max{t₁, t₂+t₃, t₂+t₄, t₃+t₄}→ min_t

Исключим t₁ и, используя симметрию по t₂,t₃,t₄ и выпуклость целевой функции, положим t₂=t₃=t₄=x.

max{1-3x, 2x}→ min  1-3x = 2x  x = ¹/₅.

N-ядро =(²/₅, ¹/₅, ¹/₅, ¹/₅) не совпадает с вектором Шепли =(¹/₂, ¹/₆, ¹/₆, ¹/₆)

Постройте вектор Шепли самостоятельно.

v-1(1)	эксцесс l(S,t)		v-1(0)	эксцесс
ЯТЮМС	1-t1-t2-t3-t4-t5=0			0
ЯТЮМ	1-t1-t2-t3-t4 =t5		С	-t5
ЯТЮ__С	1-t1-t2-t3 -t5=t4		М	-t4
ЯТ__МС	1-t1-t2 -t4-t5=t3		Ю	-t3
Я_ЮМС	1-t1 -t3-t4-t5=t2		Т	-t2
_ТЮМС	1 -t2-t3-t4-t5=t1		Я	-t1
ЯТЮ	1-t1-t2-t3 =t4+t5		МС	-t4-t5
ЯТ__М	1-t1-t2 -t4 =t3+t5		Ю С	-t3-t5
ЯТ____С	1-t1-t2 -t5=t3+t4		ЮМ	-t3-t4
Я_ЮМ	1-t1 -t3-t4 =t2+t5		Т С	-t2-t5
Я_Ю__С	1-t1 -t3 -t5=t2+t4		Т М	-t2-t4
Я___МС	1-t1 -t4-t5=t2+t3		ТЮ	-t2-t3
_ТЮМ	1 -t2-t3-t4 =t1+t5		Я С	-t3-t5
_ТЮ__С	1 -t2-t3 -t5=t1+t4		Я М	-t1-t4
Я_Ю	1-t1 -t3 =t2+t4+t5		Т МС	-t2-t4-t5
ЯТ	1-t1-t2 =t3+t4+t5		ЮМС	-t3-t4-t5

N-ядро лучше оценило силу партий, чем вектор Шепли: партии 2, 3 и 4 вместе сильнее, чем партия 1!

Пример К5. Анализ ситуации на Украине после парламентских выборов 2006 года.

В Раду прошли 5 партий, набравшие - 32% (партия регионов, лидер – Янукович), 22% (БЮТ, Тимошенко), 14% (Наша Украина, Ющенко), 5% (СПУ, Мороз) и 4 % голосов (КПУ, Симоненко).

Вопрос: На сколько мест в коалиционном правительстве должна претендовать каждая из партий?

Партии, прошедшие в Раду, набрали 77% голо­сов. Любаяая коалиция партий, набравшая 39% голосов, может формировать прави­тельство, а не вошедшие в нее партии (антикоа­лиция) – нет. Число возможных коалиций равно 2⁵. Запишем их в таблицу парами: слева потенциально правящая коалиция, справа – проигравшая антикоалиция.

Дележ: t₁+t₂+t₃+t₄+t₅=v({ЯТЮМС})=1, t_i≥ v({i})=0

Очевидно, что в парах неотрицательные эксцесс имеют коалиции слева. А в левом столбце эксцессы верхних коалиций не превосходят эксцессов нижних пяти коалиций (все их слагаемые как часть входят в эксцессы нижних коалиций). Поэтому

max _S l(S,t)= max{t₁+t₄, t₁+t₅, t₂+t₃, t₂+t₄+t₅, t₃+t₄+t₅}

Используем симметрию пар t₂,t₃ и t₄,t₅ (t₃=t₂ и t₅=t₄), и исключим t₁: max _S l(S,t)= max{1-2t₂-t₄, 2t₂, t₂+2t₄}.

Мы ищем точку минимума выпуклой верхней огиба­ющей семейства трех линейных по t₂ и t₄ функций.

Выделим области D_i, в которых огибающая совпадает с i–той функцией.

max=1-2 t₂-t₄: 1-2 t₂-t₄ > 2 t₂  t₄ < 1-4 t₂, 1-2 t₂-t₄ > t₂+2 t₄  3 t₄ < 1-3 t₂  t₄ < ¹/₃- t₂

max=2 t₂: 2 t₂ >1-2 t₂-t₄  t₄ > 1-4 t₂, 2 t₂ > t₂+2 t₄  t₂ > 2 t₄  t₄ < t₂ / 2

max=t₂+2 t₄: t₂+2 t₄ > 1-2 t₂-t₄  t₄ > ¹/₃- t₂, t₂+2 t₄ > 2 t₂  t₄ > t₂ / 2

Ограничения и сами функции – линейны,  в каждой области решаем свою задачу ЛП.

функция	Ограничения области	min
1-2 t2-t4	t4 < min { 1-4 t2 , 1/3 - t2 }	4/9
2 t2	1-4 t2 < t4 < t2 / 2	4/9
t2+2 t4	t4 > max { 1/3- t2 , t2 / 2 }	4/9

И з графика видно, что оптимум достигается в точке пересечения областей:

1-4 t₂= ¹/₃ - t₂  3 t₂ = ²/₃ 

t₂ = ²/₉   t₄ = ¹/₃ - t₂ = ¹/₉ ,

 t₁ = 1 - 2 t₂ - 2 t₄ = ³/₉ = ¹/₃

N-ядро = ( ³/₉, ²/₉, ²/₉, ¹/₉, ¹/₉).

Оно не совпадает с вектором Шепли = ( ²/₅, ⁷/₃₀, ⁷/₃₀, ¹/₁₅, ¹/₁₅).

₁() =  2/(4∙C₅⁴) + 6/(3∙C₅³) + 2/(2∙C₅²) = ²/₂₀ + ⁶/₃₀ + ²/₂₀ = ¹²/₃₀ = ²/₅,

₂() = ₃() = 1/(4∙C₅⁴) + 4/(3∙C₅³) + 1/(2∙C₅²) = ¹/₂₀ + ⁴/₃₀ + ¹/₂₀ = ⁷/₃₀ ,

₄() = ₅() =  2/(3∙C₅³) = ²/₃₀ = ¹/₁₅. Заметим, что  ¹²/₃₀ + ⁷/₃₀ + ⁷/₃₀ + ²/₃₀ + ²/₃₀ = 1.

Возможности второй и третьей партий по отдельности по созданию правящей коалиции равны возможностям партий 4 и 5, действующим совместно, и N-ядро адекватно отражает силу партий:

		t1	t2	t3	t4	t5
ЯМС	p1	0	1	1	0	0
ТЮМ	p2	1	0	0	0	1
ТЮС	p3	1	0	0	1	0
ЯЮ	p4	0	1	0	1	1
ЯТ	p5	0	0	1	1	1

t₂ = t₃ = ²/₉ = t₄ + t₅ , в то время как ₂() = ₃() = ⁷/₃₀ >> ⁴/₃₀ = ₄() + ₅() .

Можно искать t_опт как решение матричной макроигры. Один макроигрок выбирает смешанную коалицию (p_i - вероятность прихода коалиции к власти), а другой – дележ. Игра простая  t_i >0,  t_i = 1, т.е. дележ t является аналогом смешанной стратегии выбора партии q. Эксцесс l(S,t) – аналог B_i(q). Мы уже знаем t_опт. Вектор p можно найти с помощью ТДН. Все t_j>0  A_j(p) =⁴/₉ j.

A₄(p) = A₅(p)  p₂= p₃, A₁(p) =⁴/₉ p₂=²/₉ , A₂= A₃ p₄= p₅,

A₄=⁴/₉ p₄=¹/₉ , A₂=⁴/₉ p₁=³/₉ , p = (³/₉ ,²/₉ ,²/₉ ,¹/₉ ,¹/₉ ).

Д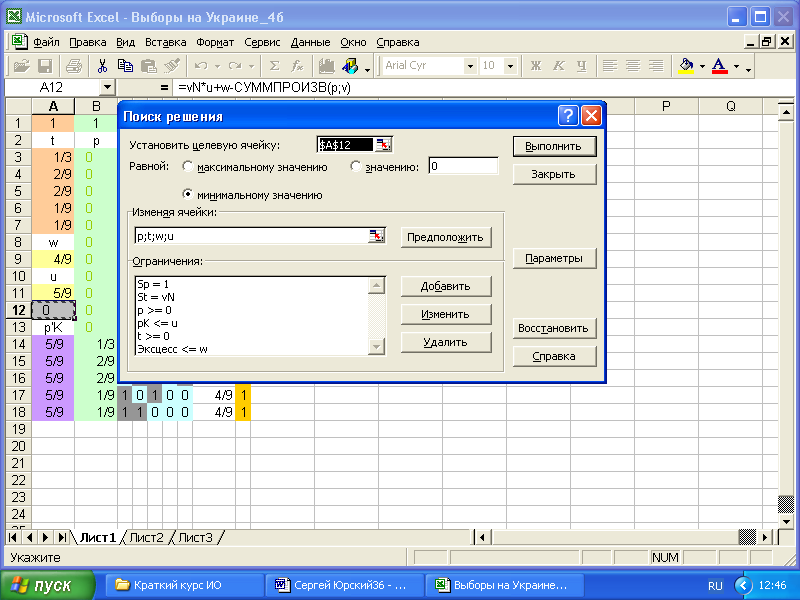 ля учета взаимоотношений между партиями (например, маловероятна коалиция Януковича и Тимошенко) можно различать выигрыши коалиций. Выигрыш (функция полезности) коали­ций конституционного большинства больше среднего, антипрезидентских – меньше. Полученную задачу ЛП небольшой размерности решаем в EXCEL командами Сервис+Поиск решения.

Сведение к ЛП: t_опт = argmin w,

при ограничениях дележа

t_i> v({i}),  t_i= v(N)

и эксцесса v(S) - Kt ≤ w

где Kt = {t_i| iS} S.

Прямая задача ЛП:

 p_i·v_i- v(N)·u → max

при p′ K ≤ u, p_i> 0,  p_i= 1.

ТДН: 1) v(S) - Kt < w  p_i= 0,

p_i> 0  v(S) - Kt = w;

2) t_i> v({i})  p′ K = u ,

p′ K < u   t_i= v({i}).

p′ K - вероятность попадания партий в правительство (сумма

вероятностей p_i всех коалиций, содержащих партию), аналог A_j(p).

Для любой партии, не являющейся болваном, вероятность попадания в правительство равна u. По теореме двойственности p_i·v(S_i) = u∙v(N) + w. Если игра простая, то v(S_i) = v(N) = 1 u+w=1.

На какую долю d_i мест в правительстве может и должна претендовать каждая из партий? t_i – это доля мест в правительстве в среднем, т.е. t_i = d_i∙u +0∙(1-u). Отсюда d_i= t_i/ u 

d_{Янукович} = (³/₉) / (⁵/₉) = ³/₅ = 60%; d_{Тимошенко} = d_Ющенко = (²/₉) / (⁵/₉) = 40%; d_Мороз = d_{Симоненко} = 20%.

Еще раз подчеркнем: решение целиком определяется подбором вектора v выигрыша коалиций!