На входе: матрицы а –пропускных способностей, и c – цен, c ij  0 - стоимость пропуска единицы потока по ребру (I,j), f0 - ограничение на величину потока.

Потоковая матрица X = { x _ij }должна удовлетворять ограничениям:

1) 0  x _ij   _ij , 2) x _js = x _tj = 0  j  s,t, 3) - баланс потока.

Мы хотим минимизировать стоимость потока при ограничении . Это неравенство можно превратить в равенство, так как мы экономим деньги и лишнего не купим, то есть F(x) = F₀.

Т.о. имеем частный случай задачи ЛП, разрешимой за полиномиальное время методом Хачияна или Левина. Но мы эту задачу будем решать иначе.

Если все числа целые, то на каждом шаге поток увеличивается на 1, и в худшем случае будет шагов F₀. Но за полиномиальное время решается задача: есть решение задачи ПМС? Предположим, что сеть может пропустить поток R.

???Алгоритм №1. «Цикл». Найдем максимальный поток и начнем его уменьшать до F₀: т.е. ищем цикл с отрицательной суммарной стоимостью (аугментальный цикл) и на цикле уменьшаем стоимость. Для этого находим максимальное _max как и в Ф-Ф, при этом стоимость падает на S= c_ij<0, если  c_ij<0, после чего ищем очередной аугментальный цикл.

Алгоритм №2. Считаем поток по каждой дуге ориентированным. В цикле находим самую дорогую в сети цепочку из s в t и по ней сократим поток.

Алгоритм №3. ДОСТРОЙКА. На каждом этапе находим самую дешевую не цепочку, а сеть из s в t (аналогично алгоритму Дейкстра) и посылаем по ней (ДК-алгоритмом) поток максимальной величины. Если у вершины окажутся 2 отца с оптимальной стоимостью, то обоих оставляем. Полученную сеть вытянем по слоям в соответствии с ценами. Часть ребер насытится, после чего они блокируются и задача решается заново.

П ример работы алгоритма ДОСТРОЙКА: F₀=16 Этап 1:

Шаги 1,2. minПСВ=1, k=2. minПСВ=1, k=4.

Все пути из S в t в этой сети имеют стоимость 13. f = ∑ ПСВ =2. S=2*13=26, F=2.

Э тап 2: После этапа 1 ребра (1,2) и (4,3) насыщены. Этап 3.

s=6*14=84, S=26+84=110 s=6*15=90 S=110+90=200

Э тап 4. По обратной дуге ранее включенная вершина 1 меняет пометку с 8 на 5!!

Можно было бы пропустить поток F = 17, но нам не нужно. Ответ – S=232.

P.S. Стоимость обратных дуг отрицательна. Это может привести к уменьшению пометок ранее включенных вершин, если добавление обратных дуг не порождает ориентированных циклов.

3.6. Приближенное решение np-полных задач.

№26. Задача о максимальном независимом множестве.

Граф: вершины=работы соединены ребром, если они используют один и тот же ресурс.

Вопрос: Какое максимальное количество работ можно выполнять одновременно?

Решение: Алгоритм типа ДОСТРОЙКА («включение членов»).

S = . Находим вершины с минимальной степенью 2: 4,5,6,8. Выбираем 4: S = {4}. Удаляем вместе с ребрами работы 3 и 5, которые не могут выполняться, если выбрана 4. Выбираем 6 степени 1: S={4,6}, удаляем 7. 2,8 степени 1, выбираем 2: S={4,6,2} удаляем 1. Осталась 8 ст. 0, S={4,6,2,8}.

Алгоритм типа развал (обратный алгоритму ДОСТРОЙКА «отстрел кандидатов»)

Сначала все вершины – кандидаты, затем начинаем удалять вершины с макси­мальной степенью: сначала – 7, корректируем степени, затем в новом графе ищем вершину с максимальной степенью – 3, удаляем

S ={7,3,1,5}, затем S=V \S={2,4,6,8} Ответ.

Задача о минимальном доминирующем множестве.

П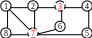 остроить min количество военных баз, контролирующих все вершины???.

Достройка: выбираем вершины с максимальной сте­пенью и удаляем уже контролируемые вершины. Затем то же делаем в оставшемся графе. Ответ: {7 и 3}.

Задача: развал самостоятельно.

№27. Задача о минимальной раскраске.

Найти минимальное число красок, при котором граф м.б. правильно раскрашен (т.е. любые 2 смежные вершины окрашены в разный цвет), и сам способ окраски.

Имеет место Теорема. Всякий планарный граф можно раскрасить в 4 краски.

Рассмотрим простой алгоритм, раскрашивающий планарный граф в 6 цветов.

Алгоритм: Удаляем вершины с минимальной степенью. В планарном графе число ребер R меньше 3N,  S_i= 2R < 6N  минимальная степень < 6.

Удаляемые вершины	4	5	3	6	2	1	7	8
Si в момент удаления	2	1	2	1	2	2	1	0
Номер краски	3	1	2	1	1	3	2	1

Теперь идем в обратную сторону и определяем номер краски: нельзя использо­вать краски, которыми окрашены соседние вершины. Т.к. в момент удаления степень вершин была меньше 3, то нам хватит 3 красок.