Ярославский государственный университет

Кафедра компьютерной безопасности и математических методов обработки информации

Фокин В.Г.

ТЕОРИЯ ИГР

И

ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

Модели, алгоритмы, сложность.

Конспект лекций

Ярославль, 2006

Хотели как лучше, а получилось как всегда.

_{Виктор Черномырдин, премьер России в 1994-1998гг}

1.1. Введение.

Термин исследование операций возник в 30-е годы ХХ века как название подраз­деления британских ВВС, занимавшегося планированием мероприятий противовоздуш­ной обороны. Как самостоятельный предмет выделился в 50-х годах и включил в себя теорию принятия решений, сетевые модели, СМО и др.

Операцией назовем систему действий, объединенных единым планом и направлен­ных на достижение определенной системы целей. Отличительные признаки операции – допустимость (отражает ограниченность ресурсов) и управляемость. Всякий допустимый выбор управляемых параметров называется решением. Цель исследования операций – предварительное количественное обоснование решений, оптимизирующих целевые функции.

ПРИМЕРЫ ЧАСТНЫХ ЗАДАЧ исследования операций:

1) Снабжение предприятий (критерий эффективности – расходы на 1 ед. сырья).

2) Постройка участка магистрали (цели - быстрее закончить, уложиться в срок).

3) Продажа сезонных товаров. 4) Расчистка дорог от снега.

5) Медицинское обследование. 6) Противолодочный рейд.

ОСНОВНЫЕ ЭТАПЫ ОПЕРАЦИОННОГО ИССЛЕДОВАНИЯ.

1. Неформальная постановка задачи.

2. Построение математической модели исследуемой системы, т.е. выбор признаков, существенных для принятия решений, и связей между ними.

3. Выбор критериев оптимизации, т.е. выбор функций f_i (x,…).

4. Имеет ли поставленная математическая задача приемлемые методы решения? Если нет  упрощаем модель или выбираем другие критерии.

5. Находим решение в рамках модели.

6. Проверка адекватности решения. Если решение неадекватно, то уточняем модель, вводя какие-либо дополнительные ограничения. Здесь требуется эксперт (критерий), способный оценить адекватность получаемых решений.

Даже если в результате исследования удается найти наилучшее решение, окончательный выбор должен делать человек, используя дополнительную информацию, не отраженную в модели. Сложность исследования состоит в подборе подходящей модели и четком формулировании целей операции.

КЛАССИФИКАЦИЯ ЗАДАЧ ИО по постановке и методам решения :

К случаю, когда D – плохо структурировано (например, целочисленно) относится большинство NP-полных задач. Для их решения используется точный метод ветвей и границ или работающие более быстро приближенные методы.

В многокритериальных задачах цели могут оказаться противоречивыми, поэтому внимание сосредотачивается на выборе критериев.

1. Выбор главного критерия, т.е. f _i0  extr при ограничениях 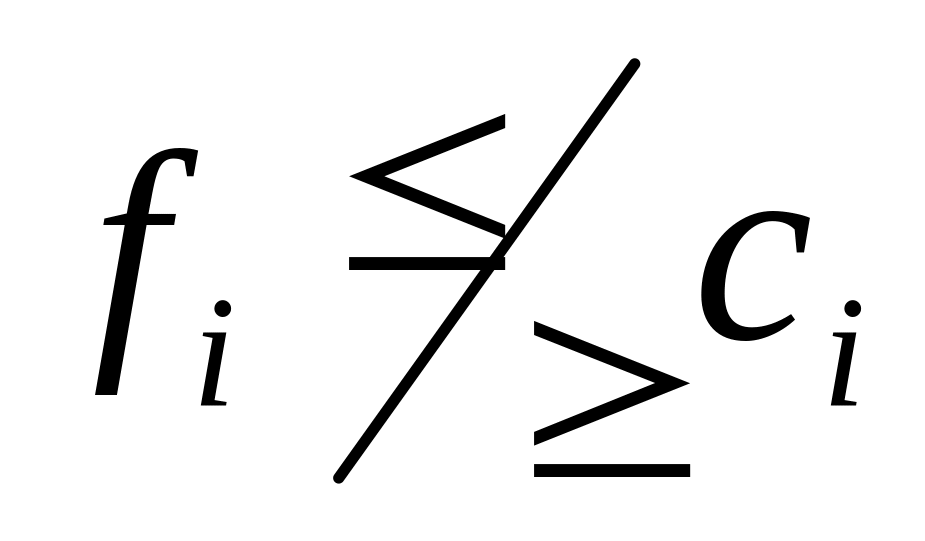для ii₀.

2. Построение свертки критериев F(x) = 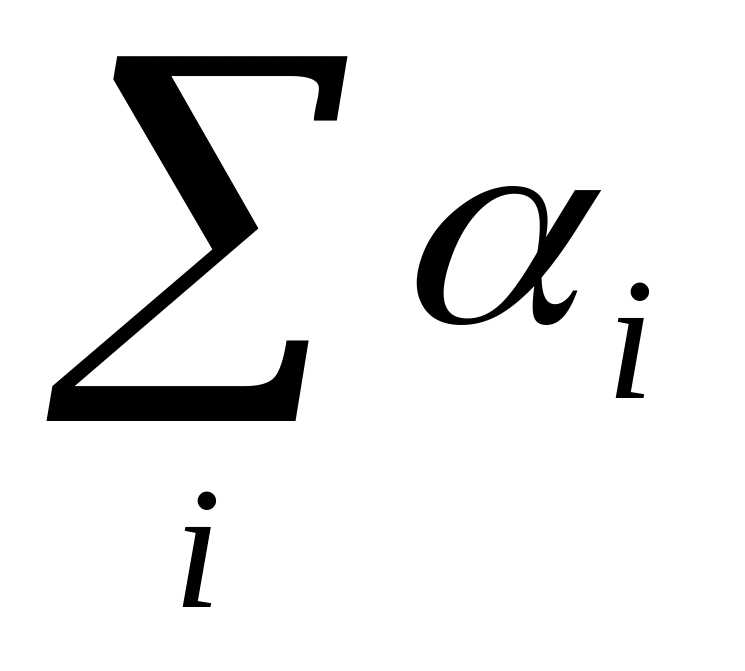· f (x), где _i – вес i-го критерия.

3. Принцип Парето (отсечение вариантов, более слабым по всем показателям).

При принятии решений в условиях неопределенности функция f зависит от неизвестного y, от которого можно избавиться следующими способами:

1. Пессимист: F(x) = 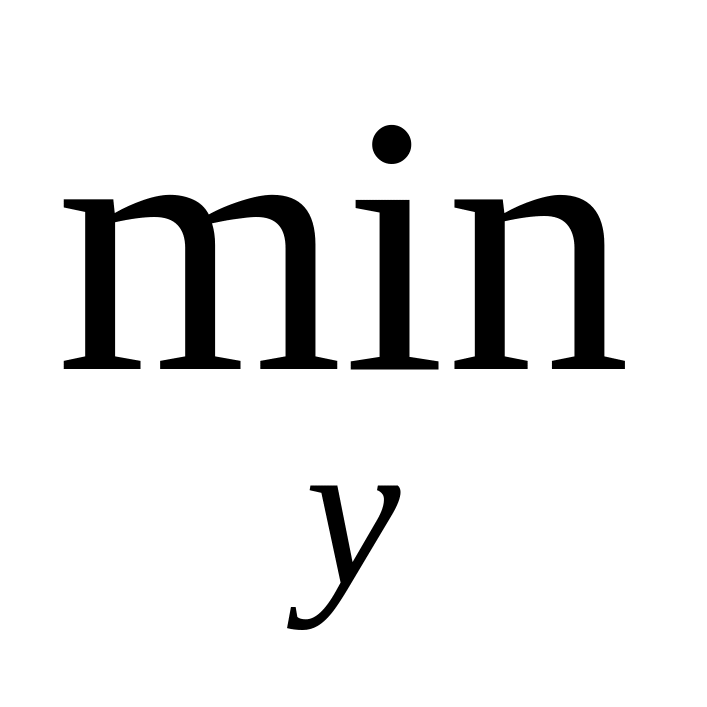f (x, y). Пример – строительство моста.

2. Оптимист: F(x) = f (x, y). Пример - снятие вратаря в хоккее.

3. Прагматик: F(x) = M_y f (x, y), здесь y рассматривается как случайная величина и M_y – оператор мат.ожидания по y. Теперь x^опт=argmax F(x) .

В играх имеется несколько активных сторон (игроков), поведение которых описывается множествами стратегий. Некоторые игроки делают выбор случайно, а остальные стремятся максимизировать свои функции полезности. Для определения наиболее разумного поведения игроков применимы принципы Парето, пессимиста (когда действия других игроков неизвестны) и Нэша (или равновесия) – когда всем игрокам невыгодно играть по-другому.

Модель принятия решений в условиях неопределенности иногда интерпретируется как игра с природой.

Типы рекуррентных уравнений и трудоемкость рекурсивных алгоритмов.

1. T_n = T_{n -1} + C·n  T_n = O(n²). (сортировка методом пузырька).

2. T_n = 2T 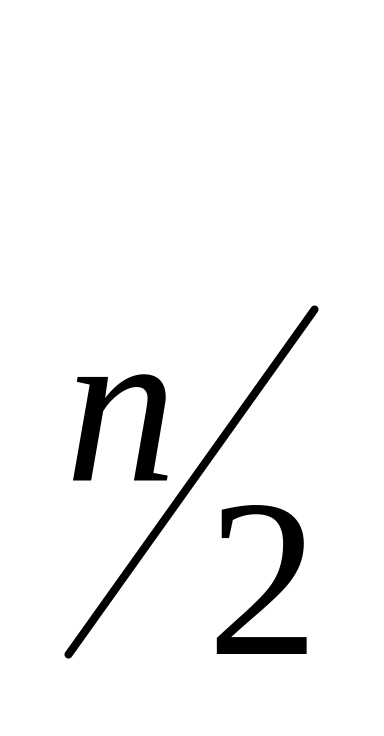+ C·n  T_n = C·n·log n (быстрая сортировка, диаграммы Вороного).

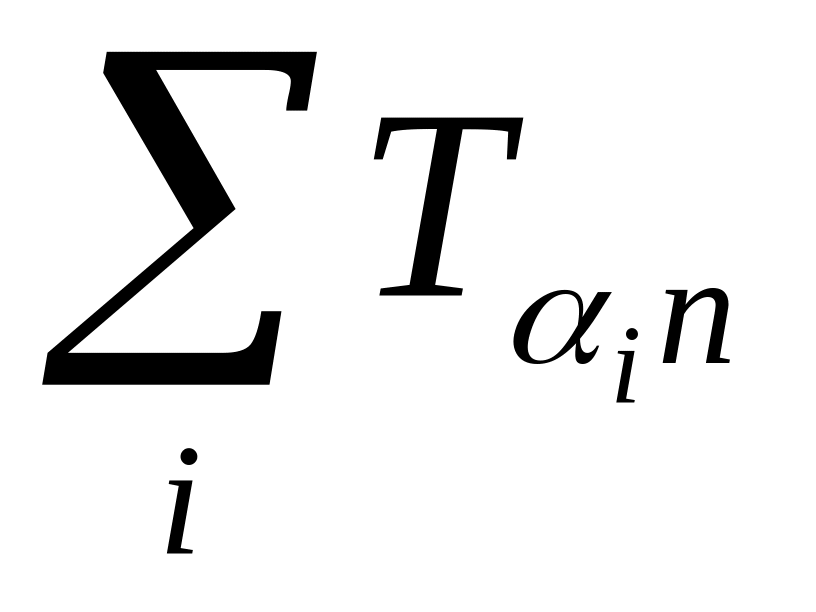3. T_n  c·n + и =  < 1,  T_n = O(n) (k-ое число, МОД, ЛП в R²).

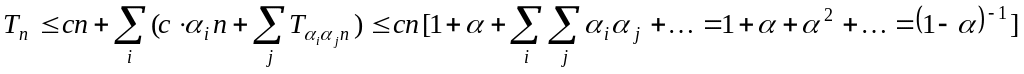
4. T_n = T_{n -1} + C  T_n = C·n (задача Штейнера).

5. T_n = T_{n -1} + k·T_{n -2}. Решение ищется в виде T_n = ⁿ  ⁿ = ^{n –1} +k·^{n -2} или

² =  + k  _1,2 = ¹/₂ ±  , а C_1,2 зависят от T₁ и T₂

Таблица 1. Зависимость трудоемкости алгоритмов от размера задачи.

n	n · log n	n2	n3	n4	2n	nn
2	2	4	8	16	4	4
4	8	16	64	256	16	256
10	32	100	1000	104	1024	1010
1000	104	106	109	1012	10300	103000

Многие оптимизационные задачи небольшого! размера (ЛП, матричные игры, ЦЛП …) легко решаются в EXCEL с помощью команд Сервис и Поиск решения.

Алгоритмы решения многих задач предполагают сортировку данных, минимальная теоре­тическая трудоемкость которой O(n·log n), т.к. угадывание одной из n! перестановок требует log(n!(n/e)ⁿ √2̃̃∙̃ñ ,Стирлинг) вопросов. Метод “пузырька” имеет трудоемкость O(n²).

Алгоритм сортировки с трудоемкостью O (n log n) в худшем случае.

Разобьем множество элементов на пары и упорядочим каждую пару. Затем склеим пары в упорядоченные четверки, потом четверки в восьмерки и т.д. Склейка производится следующим образом: записываем наименьший из меньших элементов из двух склеиваемых множеств, затем записанный элемент вычеркиваем и повторяем операцию, пока не опустеют оба множества (рекуррентное уравнение соответствует нерекуррентному алгоритму!).

Посчитаем трудоемкость: , где T_{склейки}=cn, c=const.

Пример: Даны числа: 15 3 6 24 18 13 15 5 7 81 8. Упорядочим пары чисел 3 15 6 24 13 18 5 15 7 81 8 и сольем пары в упорядоченные четверки: 3 6 15 24 5 13 15 18 7 8 81. Формируем упорядоченные восьмерки. Сравниваем первые числа четверок 3 и 5. Минимум слева  пишем его в восьмерку и сдвигаем указатель левой четверки. Далее сравниваем 6 и 5, минимум справа  в восьмерку пишем 5 и сдвигаем указатель правой четверки и т.д. Когда одна из четверок закончится, остаток другой запишем в хвост восьмерки. На выходе упорядоченные восьмерки: 3 5 6 13 15 15 18 24 7 8 81. Склеивая таким же образом восьмерки, в итоге получим упорядоченное множество: 3 5 6 7 8 13 15 15 18 24 81.

В частных случаях бывают более быстрые методы упорядочения. Например, для массива из 10⁹ элементов с целыми значениями из интервала [1,100] заведем 100 счетчиков и за линейное время посчитаем кратность каждого числа.

№2. ПОИСК k-ого элемента ЗА ЛИНЕЙНОЕ ВРЕМЯ. (Кнут, т.3, стр. 261)

1. Будем считать, что n=7*(2q+1), где q – произвольное натуральное число. Если это не выполнено, то добавим нужное число максимальных элементов.

2. Запишем данные по 7 чисел в строке и упорядочим строки по возрастанию.

3. Н айдем медиану Z в среднем столбце.

4. Фильтруем строки по среднему столбцу относительно Z, т.е. делим строки на две части: больше или меньше Z в столбце.

5. Обозначим получившиеся зоны как показано на рисунке. Очевидно, a  Z  d для всех aA и dD. Остались B и C.

6. Фильтруем все xBC относительно Z: если x  Z, то xA*, иначе xD*.

7. Пусть r  число элементов множества A+A^*. Если k=r, то искомое число равно Z. Если k<r, то ищем k-ое число в A+A^*, иначе ищем (k-r)-ое число в D+D^*. В обоих случаях остается не более ⁵ⁿ/₇ чисел.

Оценим трудоемкость этого рекурсивного алгоритма: T_n  c·n + . У нас  _i = ¹/₇ + ⁵/₇ = ⁶/₇ < 1,  T_n  7·c·n. Если в строки записывать по 5 чисел, то T_n  c·n + и  _i = ¹/₅ + ⁷/₁₀ = ⁹/₁₀  T_n  10·c·n .

7	9	3	1	6
5	18	2	4	8
9	6
1	3	6	7	9
2	4	5	8	18
6	9	18	18	18

Пример: Дан неупорядоченный массив чисел.

Разобьем массив на пятерки, упорядочим их, и допол­ним последнюю строку максимальными элементами.

В среднем столбце найдем средний по значению элемент Z=6. Фильтруем строки относительно Z по среднему столбцу и выделяем множества A,B,C,D.

2	4	5	8	18
1	3	6	7	9
6	9	18	18	18

Фильтруем BC относительно Z, формируя A*={6} и D*={8,18,9}. Позиция Z равна r = |AA*| + 1 = 7.

Если мы ищем девятое по значению число массива, то т.к. 9>r  надо искать 2-й (=9-r) элемент неупорядоченного множества D*D={8,18,9,7,9}, это 8. Лишние максимальные элементы погашены, т.к. мы знаем, сколько их добавлялось.

Задание. Придумайте алгоритм поиска 1-медианы на прямой с линейной трудоемкостью.

Структуры для хранения постоянно меняющихся данных. Их можно реализовать с помощью указателей или массивов.

Стек (магазин) работает по принципу LastInFirstOut «последним пришел – первым ушел» и обеспечивает поиск «сначала вглубь». У него есть вершина top, в начале равная нулю.

Операции со стеком: Push – добавление элемента в стек if (top == n) error “overflow” else *++top=x, Pop – выборка верхнего элемента стека if (top == 0) error “underflow” else return*top--.

0	1	top	3	4	5
м	а	м	а

При выборке сдвигается указатель на вершину стека, а сам стек не очищается!

Пример. В стек занесено 4 символа “мама”, а затем выбран 1 символ - “а”, top = 2.

Очередь работает по принципу FirstInFirstOut «первым пришел – первым ушел» и обеспе­чивает поиск «сначала вширь». У нее есть голова head и хвост tail. В начале head=tail=Q. Массив свернут в кольцо и за n следует 1. Операции с очередью: //отследить overflow и underflow

Enqueue добавление x к очереди {*tail = x; if (tail-Q==n) tail=Q else tail++} // head- tail==1 →over

Dequeue удаление x из очереди { x =*head; if (head-Q==n) head=Q else head++; return x;}

head	1	2	3	4	5	6	7	tail	9
п	а	п	а	-	м	ы	л

0	1	2	tail	head	5	6	7	8	9
у	к	и	а	-	м	ы	л	-	р

Пример. В очередь занесено 8 символов “папа-мыл”, затем выбраны 4 символа “папа” и добавлены 5 “-руки”.

А ВЛ-деревья. Двоичное дерево сбалансировано, если для каждой его вершины глубина левого поддерева отличается от глубины правого поддерева не более чем на единицу. При этом занесение в дерево и удаление из него одного элемента требует не более O(log n) операций, где n – число хранящихся в ней элементов. Если после добавления или удаления элемента баланс будет нарушен, то он сразу же восстановливается перестройкой дерева. Проверка баланса и перестройка дерева также требуют не более O(log n) операций.

В водимый Z сравниваем с корнем K. Если Z=K, то выход с сообщением «Такой элемент у нас уже есть». Иначе идем вниз (направо, если Z >K, или налево), сравнивая Z с корнем соответствующего поддерева. Если сравнивать не с чем, то заносим Z в этом месте и поднимаемся вверх по дереву, пока не встретим первую несбалансированную вершину U. Ее место займет (как показано на рисунке) вершина V, если предыдущие на пути вверх ребра (U,V) и (V,W) напрвлены в одну сторону, или вершина W, если ребра разнонаправлены.

Пример. На вход последовательно поступают цифры 1957684023. Балансировка нужна после ввода 56723. Двоичные кучи позволяют сортировать массив за O(n log n) с дополнительной памятью размера O(1) (вместо O(n) для сортировки слиянием). На их базе эффективно реализуется очередь с приоритетами.

A[1] = корень дерева Parent(i) {return ceil(i / 2)} Left(i) { return 2i } Right(i) { return 2i+1 }

Основное свойство кучи: значение потомка не превосходит значения предка A[Parent(i)]>A[i]

→ максимальный элемент кучи и любого ее поддерева находится в корне (этого поддерева).

П ример -

1	2	3	4	5	6	7	8	9	10
9	8	7	5	4	6	2	1	3	0

Heapify(A,i) {l=Left(i); r=Right(i); max = l≤heapSize && A[l]>A[i] ? l : i;

if (r≤heapSize && A[r]>A[max]) max = r; if (max ≠ i) {A[i]↔A[max]; Heapify(A,max)}}

Процедура поддерживает основное свойство кучи. Время работы – O(log n).

BuildHeap(A) { heapSize = length[A]; for (i=ceil(length[A]/2); i>0; i--) Heapify(A,i) }

Процедура cтроит кучу из исходного массива. Время – O(n).

HeapSort(A){BuildHeap(A); for (i=length[A]; i>0; i-=2){A[1]↔A[i]; heapSize--; Heapify(A,1)}}

Процедура сортирует массив, не используя дополнительной памяти. Время – O(n log n).

Процедуры, используемые при моделировании очереди с приоритетами на базе кучи. Время – O(log n).

ExtractMax(A) {if (n<1) Error; max=A[1]; A[1]=A[n--]; Heapify(A,1); return max}

Insert(A,key) { i=++n; while i>1 && A[Parent(i)]<key do A[i]=A[i=Parent(i)]; A[i]= key}

№1. Задача о p-медиане (как пример оптимизационной задачи в ¹).

Пусть точки x_i – магазины, _i – интенсивность продаж в i-ом магазине ( ). Разместим среди них p центров обслуживания c_j (складов), минимизируя функционал или . В первом случае множество C называется P-медианой, а во втором − P-центром.

Рассмотрим наиболее простой случай, когда все точки лежат на прямой, упорядочены, p=1 и единственный центр c размещен на отрезке [x_k, x_k+1]. Тогда

. Решение задачи свелось к минимизации на отрезке линейной по c функции:

1. если Δ_k< 0, то размещаем центр в точке x_k+1, если Δ_k> 0, то в точке x_k;

2. если же Δ_k= 0, то центр можно разместить в любой точке отрезка [x_k, x_k+1].

Отсюда вытекает алгоритм отыскания 1-медианы на прямой: движемся по прямой слева направо, подсчитывая Δ_k на каждом интервале и перемещая центр в правый конец интервала, пока Δ_k не станет меньше 0. Т.е. W_k= > S=(W_n / 2).

Отметим, что здесь важны не расстояния между точками, а порядок точек!!

Пример: Пусть 6 пунктов упорядоченны по координате x и общий вес W₆=195.

i	30	15	40	60	18	32
Wk		45	85	145

S=W₆/ 2=97,5; W₁=30<S  переходим к пункту 2;

W₂=30+15=45<S; W₃=45+40=85<S; W₄=85+60=145>S  размещаем центр в последнем рассмотренном пункте 4.

Можно предположить, что и для p–медианы расстояния не играют роли. Это неверно. Пусть n=6, p=2, все w_i=1, x_i=i  C={2,5}, но если x₆=9, то C={3,6}.

i	wi	c1	Fi1	ji2	c2	Fi2	ji3	c3	Fi3
0	1	5	129	5	2	62	4	2	36
1	8	5	124	5	2	60
2	8	5	92	6	4	44
3	4	6	66	6	4	28
4	8	6	54	7	5	22
5	8	7	32	7	5	14
6	4	7	16	8	7	6
7	8	8	10	8	7	2
8	8	8	2	9	8	0
9	2	9	0

Пример 2. Построение 3-медианы методом динами­ческого программирования. Пусть x_i=i. w_i – см. таблицу.

Значение критерия при оптимальном размещении

1-го центра на интервале [x_i, x_j) = f_ij,

k центров на интервале [x_j, ∞) = F_jk.

Таблица заполняется слева направо и снизу вверх.

Трудоемкость равна O(n²p), а если использовать выпуклость F_jk по параметру j, то O(np·log n).

Например, F₂₂ = min{3: 0+66, 4: 4+54, 5: 16+32=48, 6: 28+16=44,…} = 44.

F₀₃ = min{1: 0+60, 2: 1+44, 3: 9+28=37, 4: 14+22=36, 5: 30+14,…} = 36.

В скобках до двоеточия стоит j - точка раздела зон, а после двоеточия - f_ij + F_jk.

Изменив критерий, упростим поиск одного центра: минимум функционала _i x_i-c² достигается в точке z = _i·x_i/ _i - центре тяжести множества X.

_i x_i-c² = _i x_i-z² +_i z-c² +2_i (x_i-z, z-c).

Но z-c не зависит от i, а _i (x_i-z) = _i·x_i-_i_i·x_i/ _I =0  слагаемое3 = 0. Если точки равномерно покрывают компактную область и веса примерно равны, то решения задач с обоими критериями очень близки. ???